
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные алгоритмы и поиск трассы основные алгоритмы
|
|
Алгоритм Ли
Основная идея алгоритма формулируется следующим образом. Имеем сеть, по дугам которой возможно прохождение трассы трубопровода. Поиск оптимальной трассы — многошаговый процесс. На каждом шаге алгоритма исследуются все пробные пути, построенные от начальной точки трассы, и устанавливается путь с наименьшей стоимостью. Этот путь в данный момент является наиболее перспективным. Надстраиваем его на одну новую дугу во всех допустимых сеткой направлениях. Получаем несколько дополнительных путей, каждый из которых представляет собой увеличенный на одну дугу путь, который мы только что считали наиболее перспективным. Затем среди всех построенных к настоящему моменту путей ищем новый наиболее перспективный и надстраиваем его на одну новую дугу во всех допускаемых сеткой направлениях. Этот процесс продолжается до тех пор, пока среди сформированных последовательной надстройкой путей не окажется путь, оканчивающийся последней точкой трассы и имеющий минимальную стоимость по сравнению со стоимостями всех сформированных к этому моменту путей. Этот путь (их может оказаться несколько) и будет оптимальным. Эта идея послужила основой для реализации алгоритмов поиска оптимальной трассы на сетках прямоугольной и произвольной конфигураций. Реализация алгоритма производится с помощью двух списков и и v. Каждый список содержит набор занумерованных строк, «стоимости» дуги (под «стоимостью» дуги понимается величина критерия оценки трубопровода по данной дуге) и направления ее входа в узел. В список и в первую строку записываем данные о начальной точке, а в список v — данные о ее «соседях». Выбираем из списка v точку с наименьшей стоимостью достижения и переносим ее в список и, вычеркивая одновременно из списка v. Таким образом, в списке и появляется вторая точка, для которой в списке v записываются данные о всех соседях. Опять выбирается из всех точек точка с наименьшей стоимостью и т. д., до тех пор, пока в список и не попадет конечная точка. В заключение по направлениям входа восстанавливается путь наименьшей стоимости.
Алгоритм представляет собой 4 шага.
Шаг 0. Полагаем, что узел Ns принадлежит дереву; Lss = 0; для соседних с Ns узлов Lst = lst; для остальных Lst = oo.
Шаг 1. Полагаем Ls = minL'st = LSj + ljF, где Nt — все узлы, соседние с текущим деревом. Дуга Ajt включается в число ветвей дерева.
Шаг 2. Если число ветвей дерева п=1, то конец поиска; если нет— перейти к шагу 3.
Шаг 3. L'st t= rnin(L'sj, LsF + lFt) —перейти к шагу 1.
Выбор оптимальной трассы и кратных трасс на сетке между двумя точками
Поиск оптимальной трассы
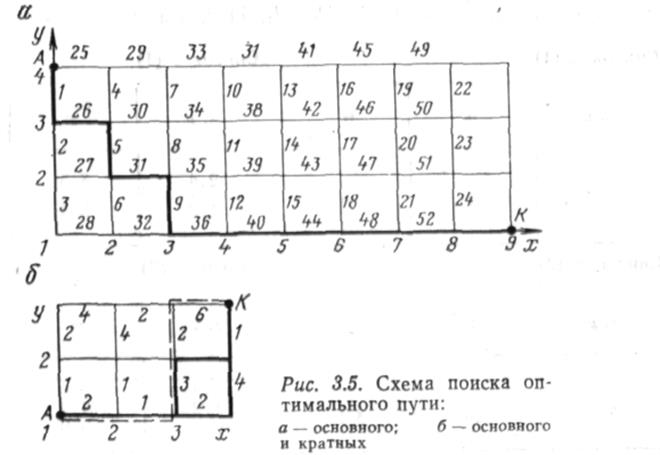
Рассмотрим поиск оптимальной трассы на сетке прямоугольной формы без диагоналей (рис. 3.5, а). Допустим, что стоимость строительства трубопровода вдоль каждой их дуг сетки оценена каким-либо условным числом w. Эти числа-стоимости приведены в табл. 3.1, а номера дуг указаны на рис. 3.5, а. Поиск оптимальной трассы будем осуществлять в соответствии с алгоритмом, основная идея которого заключается в следующем. Процесс поиска многошаговый. На первом шаге вводим в рассмотрение все возможные пути из начальной точки Л, имеющей координату (1,4), и продолжаем путь, имеющий наименьшую стоимость. На каждом последующем шаге определяем стоимость всех построенных к этому моменту путей от начальной точки и оставляем тот из них, который имеет наименьшую стоимость. Продолжаем на следующем шаге именно
| Таблица 3.1. Условная стоимость дуг |

|
этот путь, достраивая его во всех допускаемых сеткой направлениях на одну дугу. Получаем несколько новых путей. Из всех путей (с учетом отброшенных ранее) опять продолжаем наиболее перспективный путь до тех пор, пока в рассмотрение не попадет конечная точка. Решение заканчиваем отысканием такой трассы между начальной и конечной точками, для которой полный критерий оптимальности будет наименьшим. Решение проводим с помощью двух списков и и v, в которые записываем координаты х, у точки (или узла), а также направление входа в этот узел 8. На первом шаге записываем в список u (1) точку A (1,4) с w = 0 (направление входа в начальную точку безразлично), определяем для А соседние узловые точки и с соответствующими характеристиками заносим в список v (1). Направление входа в узел 9 может иметь четыре значения, которые условно обозначаем 0, 1/4, 1/2, 3/4. Причем O = 0 — это направле-
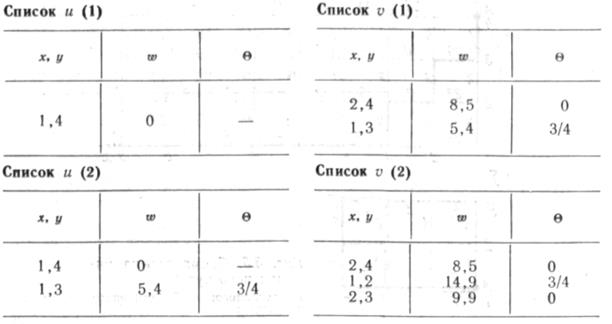
ние, определяемое осью х, а отсчет угла осуществляется против часовой стрелки. Определяем в v(\) точку с минимальным значением w и переносим эту точку в список v (2). Далее в список 0(2) помещаем все соседние с ней точки и их характеристики. В результате получаем список u (2) и список v (2).
Из списка v (2) на каждом шаге вычеркиваем точки, совпадающие по координатам с перенесенной в список у точкой, но имеющие большие значения w.

|

|
Продолжаем заполнение списков. В результате второго шага получаем
| В результате третьего шага получаем |
| Этот процесс продолжается до тех пор, пока конечная точка не окажется в списке и. Чтобы не загромождать изложение, приводим окончательный список и. |

|
| По направлению входа O в точки последнего списка и восстанавливаем оптимальный путь |
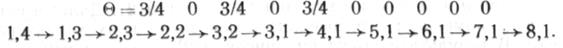
|
Как видно из последнего списка «, этому пути соответствует минимальное значение суммы чисел, оценивающих дуги, при прохождении точки А (1, 4) в точку K (8, 1) равное 36,4; то же значение получаем, если просуммировать стоимости всех дуг оптимального пути.
Поиск кратных трасс
Найденный на сетке путь наименьшей стоимости в приведенном примере является единственным. Однако в некоторых случаях таких путей с наименьшей стоимостью может оказаться несколько, и они при поиске должны быть найдены. В этом случае при выборе одной трассы будут учитываться и другие факторы, например расстановка перекачивающих станций, наличие дорог и т. п. В рассмотренном числовом примере мы закончили поиск получением первого пути, обладающего наименьшей стоимостью. В соответствии с алгоритмом на каждом шаге продолжается надстройка пути, который обладает наименьшей стоимостью. Однако все остальные возможные пути запоминаются (они зафиксированы в списках u и v) и используются при последующих шагах поиска. Если путь наименьшей стоимости найден, то можно продолжать поиск и надстраивать пробные пути (кроме уже пришедшего в конечную точку) до тех пор, пока конечной точки не достигнет какой-либо следующий путь. Путь, достигший конечной точки первым, называем первым по оптимальности, достигший вторым — вторым по оптимальности и т. д. Каждый последующий по оптимальности путь будет иметь большую, чем предыдущий, стоимость.
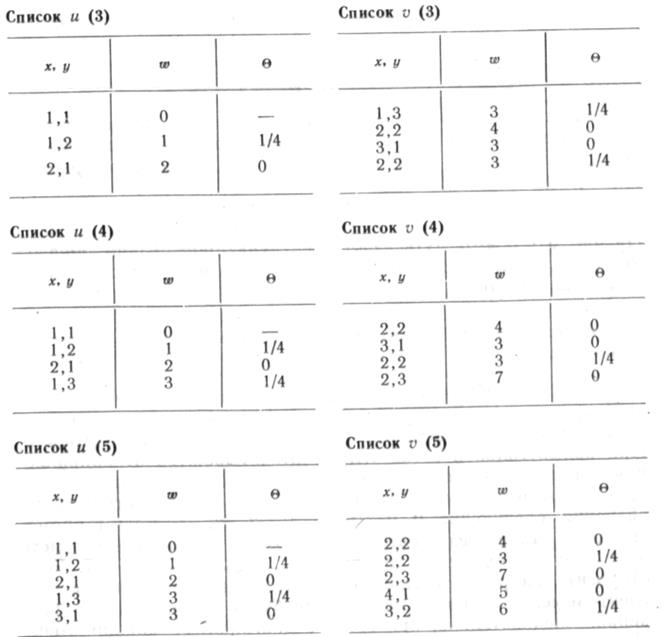
Рассмотрим поиск оптимальной и кратных трасс на сетке, изображенный на рис. 3.5, 6. Условные стоимости строительства трубопровода вдоль каждой из дуг приведены на рисунке на всех дугах. Начальная точка — A(1, 1), конечная — K(3, 4). Как и в предыдущем примере, поиск ведем с помощью списков и и v. На первом шаге в списке u (1) записываем начальную точку А с координатами (1,1), а в списке v (1) —соседние точки с координатами (1,2) и (2,1) с соответствующими стоимостями w и направлениями входа O.
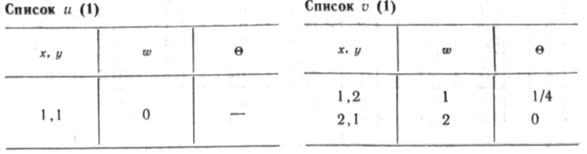
На втором шаге из списка v (1) переносим в список u (2) путь наименьшей стоимости с данными w и 0 — путь из узла (1,1) в узел (1, 2). Из списка v(\) эту точку вычеркиваем. В список v (2) заносим точки, являющиеся соседними с точкой 1,2.

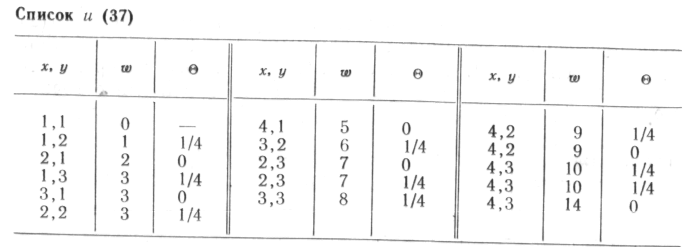
Результаты третьего, четвертого, пятого и последнего — тридцать седьмого шага приведены в списках u (3), v (3); u (4), v(4); и(5), v(5);и(37).
|
|
Восстановление оптимального пути проводим по последнему списку u (37). Как видно, точка K достигнута двумя равноценными путями с w=10, оба с направлением входа 0 = 1/4. По этому направлению ближайшим узлом обоих путей является точка 4,2. Здесь один путь уходит по направлению O =1/4 в точку 4,1, а другой — по направлению 6 = 0 в узел 3,2. Дальнейшее движение путей понятно из списка u (37). Для наглядности каждый из путей имеет свой индекс. Таким образом, имеем следующие два одинаковых по стоимости пути с w =10:
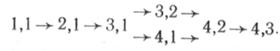
Если продолжать рассматривать пути, то уже на следующем шаге находим путь с w =14, это путь второй кратности. Восстанавливая его по направлениям входа, находим траекторию пути:
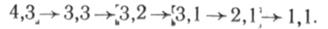
На рис. 3.5, б этот путь изображен пунктиром. Таким образом можно получить и все остальные пути, которые будут иметь большую кратность.
Поиск оптимальной трассы на прямоугольной сетке с диагоналями
Такая сетка изображена на рис. 3,2, б. Как видно из предыдущих примеров, при составлении списков и и v каждую дугу характеризуют две величины — стоимость w и угол входа 6. При прямоугольной сетке углы 0 отсчитываются от направления х против часовой стрелки. В случае сетки с диагоналями отсчет 8 ведется также от оси х против часовой стрелки, но значения следующие: 0, 1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8- Если в прямоугольной сетке без диагоналей каждая точак может иметь лишь 3 соседних точки, то при сетке с диагоналями — 7. Если отбросить из рассмотрения пути назад как заведомо бесперспективные, то сетка с диагоналями будет допускать 5 направлений. Следовательно, при сетке с диагоналями каждая точка в списке и может иметь по 5 соседних точек, заносимых в список v. Это и является основным отличием поиска оптимального пути на сетке с диагоналями от сетки без диагоналей.
Date: 2015-06-07; view: 1030; Нарушение авторских прав