Гармонические колебания. Математический маятник

Маятником является всякое тело, подвешенное так, что его центр тяжести находится ниже точки подвеса. Строго говоря, существуют только физические маятники. Но если маятник представляет собой груз, подвешенный на нити, масса которой пренебрежимо мала по сравнению с массой груза, т.е. он может рассматриваться как материальная точка, то такой маятник может быть рассмотрен как математический.

Для вывода формулы периода математического маятника заставим его описывать конус. Теперь, если мы будем наблюдать за маятником сбоку, то увидим, что маятник будет колебаться влево вправо. Но, так как все-таки он движется по окружности, то период будет равен: T = 2пr/v (1). При малых углах, возвращающая сила (P1) направлена по радиусу, т.е. равна силе P1=mv2/r (2). Из подобия треугольников OBC и DBE следует что BE/BD = CB/OB т.к. OB = l и BD = P = mg, то отсюда P1 = mgr/l (3) приравняв части получившихся формул 2 и 3: mv2/r = mgr/l, получим что v = rvg/l (4) теперь подставим значение скорости из формулы 4 в формулу 1 получим T = 2пvl/g Т.е. период математического маятника зависит только от длины подвеса (на одной географической широте).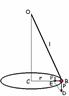
Значит, зная период колебаний маятника и длину подвеса мы можем определить значение ускорения свободного падения. Но следует заметить, что такой способ измерения ускорения свободного падения не является достаточно точным.

20. Гармонические колебания. Физический маятник. Физический маятник – это твердое тело, имеющее возможность качаться под действием его силы тяжести mg вокруг неподвижной горизонтальной оси О, не проходящей через центр тяжести тела и называемой осью качания маятника. Центр тяжести маятника совпадает с его центром инерции. Дифференциальное уравнение гармонических колебаний имеет вид: dx/dt+w₀²x=0, а его решение x=A₀cos (wt+£), где A₀-амплитуда колебаний угла x, а w=Ö(mgd/Y) и Т=2Пw=Ö(Y/mgd) – циклическая частота и период малых колеб. физ. маятника.

Физический маятник - твердое тело, совершающее колебания в гравитационном поле вокруг горизонтальной оси подвеса, расположенной выше его центра тяжести.
В соответствии с основным законом динамики вращения M=Je в общем случае для физического маятника момент силы M=Fl, а касательное ускорение равно ak=εl

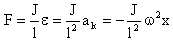
Для гармонических колебаний F=-mg/1*x, но из основного закона динамики вращательного движения F=-J/12w2x. Приравнивая выражения для силы, получаем частоту и период колебаний физического маятника:
, .

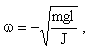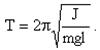Date: 2015-05-04; view: 727; Нарушение авторских прав