Теоретические сведения. Пусть и – дизъюнкты. Дизъюнкт называется резольвентой дизъюнктов D1 и D2 по переменной А и обозначается через resA(D1,D2)

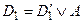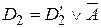Пусть и – дизъюнкты. Дизъюнкт 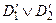называется резольвентой дизъюнктов D ₁ и D ₂ по переменной А и обозначается через res _A(D ₁, D ₂). Резольвентой дизъюнктов D ₁ и D ₂ называется резольвента по некоторой переменной и обозначается через res (D ₁, D ₂), res (A, 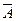)=0. Если дизъюнкты D ₁ и D ₂ не содержат контрарных переменных, то резольвент у них не существует.

Пример. Если 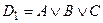, , 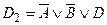то 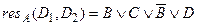, , 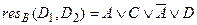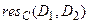не существует.

Утверждение. Если 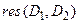существует, то ├─ .

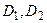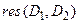Пусть 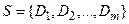– множество дизъюнктов. Последовательность формул 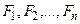называется резолютивным выводом из S, если для каждой формулы 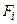(i =1,…, n) выполняется одно из условий:

1) ;

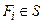2) существуют 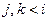такие, что .

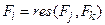Теорема (о полноте метода резолюций). Множество дизъюнктов S противоречиво в том и только в том случае, когда существует резолютивный вывод из S, заканчивающийся 0.

Существует эффективный метод логического вывода – метод резолюции. Он основан на том, что выводимость формулы В из множества посылок F ₁, F ₂, F ₃, …, F_n равносильна доказательству теоремы

├─ (F₁ Ù F₂ Ù F₃ Ù... Ù F_n ® B),

формулу которой можно преобразовать так:

├─ (F₁ Ù F₂ Ù F₃ Ù... Ù F_n ® B)

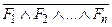├─ ( Ú B)

├─ .

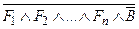Следовательно, заключение В истинно тогда и только тогда, когда формула F₁ Ù F₂ Ù F₃ Ù... Ù F_n Ù 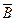º0. Это возможно при значении 0 хотя бы одной из подформул F_i или .

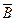Для анализа этой формулы все подформулы F_i и 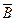должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные литеры) формируют третий дизъюнкт – резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустую резольвенту. Наличие пустого дизъюнкта свидетельствует о выполнении условия

F₁ Ù F₂ Ù F₃ Ù... Ù F_n Ù 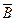º0.

Опишем пошагово алгоритм вывод по методу резолюций.

Шаг 1. Придать отрицание заключению, т. е. .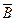

Шаг 2. Привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме.

Шаг 3. Выписать множество дизъюнктов всех посылок и отрицания заключения S = { D ₁, D ₂, …, D_k }.

Шаг 4. Выполнить анализ пар множества S по правилу:

«если существуют дизъюнкты D_i и D_j, один из которых (D_i) содержит переменную А, а другой (D_j) – контрарную переменную 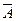, то соединить эту пару логи­ческой связкой дизъюнкции (D_i Ú D_j) и сформировать новый дизъюнкт – резольвенту, исключив контрарные литеры А и ».

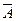Шаг 5. Если в результате соединения дизъюнктов, содержащих контрарные литеры, будет получена пустая резольвента – 0, то конец, в противном случае включить резольвенту в множество дизъюнктов S и перейти к шагу 4.

Примеры.

1. Работа автоматического устройства, имеющего три клапана А, В и С, удовлетворяет следующим условиям: если не срабатывают клапаны А или В или оба вместе, то срабатывает клапан С; если срабатывают клапаны А или В или оба вместе, то не срабатывает клапан С. Следовательно, если срабатывает клапан С, то не срабатывает клапан А.

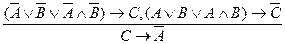
1) 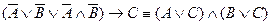– посылка;

2) 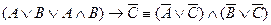– посылка;

3) 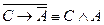– отрицание заключения;

4) множество дизъюнктов: S ={(А Ú C), (B Ú C), 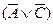, , 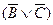C, А }.

Построим резолютивный вывод, заканчивающийся 0.

1) .

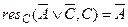2) .

Так доказано, что если срабатывает клапан С, то не срабатывает клапан А.

2. Доказать истинность заключения

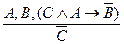
1) A – посылка;

2) B – посылка;

3) 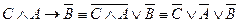– посылка;

4) 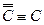– отрицание заключения;

5) множество дизъюнктов: S ={ A, B, (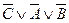), C };

6) ;

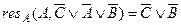7) S ₁={ A, B, (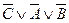), C, ()};

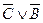8) ;

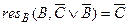9) S₂ ={ A, B, (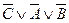), C, (), };

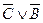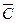10) – пустая резольвента.

Так доказана истинность заключения 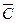по методу резолюции.

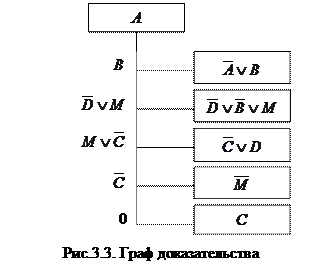
Для иллюстрации вывода удобно исполь­зовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а концевыми вершинами ветвей – оставшиеся дизъюнкты отрицания заключения и всех посылок. Узлами графа типа дерево являются резольвенты. Ниже дан пример, сопровождаемый графом.

Пример. Составить таблицу истинности. Доказать истинность заключения по методу резолюции и нарисовать граф вывода пустой резольвенты.

Решение. Образуем конъюнкцию посылок, т.е. 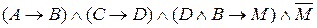. Образуем импликацию от конъюнкции посылок до заключения:

F= .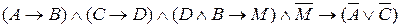

Для полученной формулы составим таблицу истинности.

Замечание. Если полученная формула является тождественно истинной, то заключение выводимо из посылок, иначе не выводимо.

Докажем истинность заключение по методу резолюций.

1) 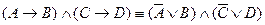– посылка;

2) 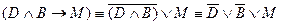– посылка;

3) 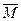– посылка;

4) 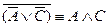– отрицание заключения;

5) S ={ A, C, , , , }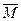

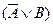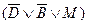6) ;

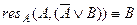7) ;

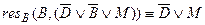8) ;

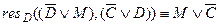9) ;

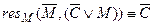10) 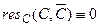– пустая резольвента.

Так доказана истинность заключения 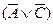, граф доказательства изображен на рис.3.3.

Замечание. Метод резолюций достаточен для обнаружения возможной выполнимости данного множества – дизъюнктов S. Для этого включим в S все дизъюнкты, получающиеся при резолютивном выводе из S. Из теоремы о полноте метода резолюций вытекает

Следствие. Если множество дизъюнктов S содержит резольвенты всех своих элементов, то S выполнимо тогда и только тогда, когда 0Ï S.

Date: 2015-06-06; view: 714; Нарушение авторских прав