Практическая часть работы

2.1. ЛОГИЧЕСКОЕ СЛЕДСТВИЕ

Теоретические сведения

Формула X алгебры высказываний называется логическим следствием формул , если импликация X₁ÙX₂Ù Ù...Ù X_n ® X является тавтологией. В этом случае говорят, что из следует X и этот факт записывают в виде .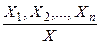

Рассуждения называются правильными, если из конъюнкции посылок следует заключение. Для определения правильности рассуждений по схеме 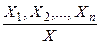требуется установить

тождественную истинность формулы X₁, X₂,..., X_n ® X.

Распространенными схемами правильных рассуждений являются следующие:

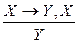– условно-категорический силлогизм;

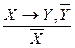– условно-категорический силлогизм;

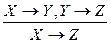– гипотетический силлогизм.

Алгоритм 2.1

(проверка, является ли данная формула X

логическим следствием формул )

1. Образуется конъюнкция посылок .

2. Составляется импликация X₁ Ù X₂ Ù...Ù X_n ® X.

3. Полученная формула исследуется на тождественную истинность: если она является тождественно истинной, то X является логическим следствием формул X₁, X₂,..., X_n, иначе – не является.

Пример.

Если два числа равны, то, как известно, их модули равны. Данные числа не равны. Можно ли из этого заключить, что их модули не равны?

Рассмотрим следующие элементарные высказывания: «Два числа равны» - X, «Модули чисел равны» - Y. Тогда высказыванию «Если два числа равны, то, как известно, их модули равны» соответствует формула X ® Y, высказыванию «Данные числа не равны» - `X, высказыванию «Модули чисел не равны» - `Y. Заметим, что вопрос задачи сводится к проверке правильности рассуждений, то есть является ли `Y логическим следствием посылок `X и X ® Y:

X®Y, `X. Составив таблицу истинности формулы

`Y

(X®Y)Ù`X®`Y, можно увидеть, что она не является тождественно истинной, следовательно, рассуждения не являются правильными, и утверждение «Модули чисел не равны» не верно.

С помощью СКНФ можно решить более общую задачу построения всех логических следствий из данных посылок.

Алгоритм 2.2

(определение всех логических следствий из данных посылок)

1. Образуется конъюнкция всех посылок .

2. Полученная конъюнкция приводится к СКНФ.

3. Множество всех формул, равносильных следствиям из данных посылок, образуют произведения сомножителей СКНФ, взятых по одному, по два и так далее.

Пример. Найти все следствия из посылок 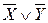и 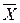Ù Y Ú X Ù .

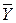Образуем конъюнкцию посылок и найдем ее СКНФ.

(`X Ú`Y)Ù(`X Ù Y Ú X Ù`Y)º(`X Ú`Y)Ù(X Ú Y)Ù(`X Ú`Y)º

º(`X Ú`Y)Ù(X Ú Y) – СКНФ. Тогда следствиями являются

`X Ú`Y; X Ú Y; (`X Ú`Y)Ù(X Ú Y).

СКНФ позволяет решить и обратную задачу: для данной формулы найти все посылки, логическим следствием которых она является.

Алгоритм 2.3

(определение всех посылок, логическим следствием

которых является данная формула)

1. Данная формула приводится к СКНФ.

2. Составляются ее произведения с каждым из недостающих до соответствующей полной СКНФ множителей – по одному, по два и так далее (под полной понимается СКНФ тождественно ложной формулы с теми же переменными).

Пример.

Следствием каких посылок является импликация X®Y?

Для импликации X®Y СКНФ имеет вид `XÚY. Соответствующая полная СКНФ имеет вид (X Ú`Y)Ù(`X Ú Y)Ù

Ù(`X Ú`Y)Ù(X Ú Y). Образуем всевозможные произведения с недостающими сомножителями:

(`X Ú Y)Ù(X Ú Y) º Y;

(`X Ú Y)Ù(X Ú`Y) º X«Y;

(`X Ú Y)Ù(`X Ú`Y) º`X;

(`X Ú Y)Ù(X Ú Y) Ù (X Ú`Y) º X Y;

(`X Ú Y)Ù(X Ú Y) Ù(`X Ú Y) º XY;

(`X Ú Y) Ù (X Ú`Y) Ù(`X Ú`Y) º XY;

(`X Ú Y)Ù(X Ú Y) Ù(`X Ú Y) Ù(`X Ú`Y) º 0.

Задание 1

Определить все логические следствия из данных посылок.

№ варианта	Посылки	№ варианта	Посылки
	,		, .
	, .		,
	,		,
	, .		,
	, .		,
	,		,
	,		,
	,		,
	,		, .
	,		,

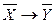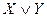
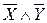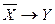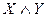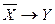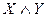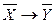
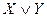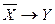
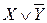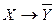
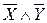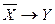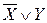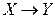
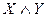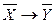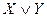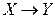
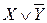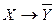
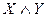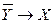
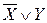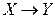
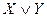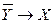
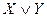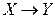
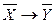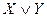
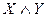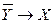
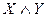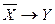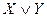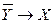
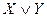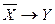
Задание 2

Определить все посылки, логическим следствием которых является данная формула.

Вариант	Заключение	Вариант	Заключение
			.
			.
			.

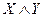
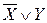
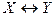
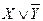
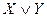
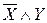
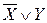
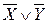
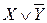
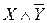
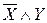
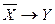
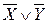
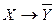
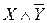
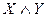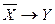
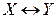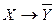
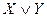Date: 2015-06-06; view: 680; Нарушение авторских прав