Теория информации К. Шеннона

В 40-е гг. прошлого столетия американский ученый К. Шеннон, специализировавшийся в вопросах пропускной способности каналов связи и кодирования сообщений, придал мере количества информации более универсальную форму: количество информации стало пониматься как величина энтропии, на которую уменьшается общая энтропия системы в результате получения этой системой информации. Формула эта выражает энтропию через сумму целого ряда вероятностей, помноженных на их логарифмы, и относится только к энтропии (неопределенности) сообщения.

Энтропия – количественная мера неопределённости, снимаемой при получении ниформации.

Иными словами, информативность сообщения обратно пропорциональна его очевидности, предсказуемости, вероятности: чем менее предсказуемо, неочевидно и маловероятно сообщение, тем больше информации оно несет для получателя. Совершенно очевидное (с вероятностью, равной 1) сообщение столь же пусто, сколь полное отсутствие такового (т. е. сообщения, вероятность которого заведомо равна 0). Оба они, согласно допущению Шеннона, неинформативны, не несут получателю никакой информации. По ряду причин, относящихся к математике и связанных с удобствами формализации, энтропия сообщения описывается Шенноном как функция распределения случайных величин.

Статья «Математическая теория связи», была опубликована в 1948 году и сделала Клода Шеннона всемирно известным. В ней Шеннон изложил свои идеи, ставшие впоследствии основой современных теорий и техник обработки передачи и хранения информации. Результаты его работ в области передачи информации по каналам связи запустили по всему миру огромное число исследований. Шеннон обобщил идеи Хартли и ввел понятие информации, содержащейся в передаваемых сообщениях. В качестве меры информации передаваемого сообщения М, Хартли предложил использовать логарифмическую функцию 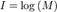. Шеннон первым начал рассматривать передаваемые сообщения и шумы в каналах связи с точки зрения статистики, рассматривая как конечные множества сообщений, так и непрерывные множества сообщений.

Развитая Шенноном теория информации помогла решить главные проблемы, связанные с передачей сообщений, а именно: устранить избыточность передаваемых сообщений, произвести кодирование и передачу сообщений по каналам связи с шумами.

Решение проблемы избыточности подлежащего передаче сообщения позволяет максимально эффективно использовать канал связи. К примеру, современные повсеместно используемые методы снижения избыточности в системах телевизионного вещания на сегодняшний день позволяют передавать до шести цифровых программ коммерческого телевидения, в полосе частот, которую занимает обычный сигнал аналогового телевидения.

Решение проблемы передачи сообщения по каналам связи с шумами при заданном соотношении мощности полезного сигнала к мощности сигнала помехи в месте приема, позволяет передавать по каналу связи сообщения со сколь угодно малой вероятностью ошибочной передачи сообщения. Также, это отношение определяет пропускную способность канала. Это обеспечивается применением кодов, устойчивых к помехам, при этом скорость передачи сообщений по данному каналу должна быть ниже его пропускной способности.

Date: 2015-06-06; view: 862; Нарушение авторских прав