Понятие предиката и кванторных операций

В алгебре логики высказывания структура высказываний и их содержание во внимание не принимаются. В то же время существуют рассуждения, зависящие от содержания используемых в них высказываний. Например, всякий ромб - параллелограмм; АВСМ - ромб, следовательно, АВСМ - параллелограмм. Таким образом, возникает необходимость в построении такой логической системы, средствами которой можно анализировать структуру утверждений, составленных из элементарных высказываний. Такой логической системой является логика предикатов, содержащая логику высказываний в качестве своей части.

В логике предикатов элементарное утверждение расчленяется на субъект (подлежащее) и предикат (сказуемое). Субъект - это то, о чем что-то утверждается в высказывании; предикат это то, что утверждается о субъекте. Например, в высказывании «6 - четное число», 6 - субъект; четное число- предикат. Заменим число 6 переменной х, получим утверждение «х - четное число». При одних значениях х это утверждение даёт истинные высказывания, а при других значениях х - ложные высказывания. Последнее утверждение является функцией одной переменной, определенной, например, на множестве N, и принимающей значения на множестве {0,1}.

Определение 1.1. Одноместным предикатом Р (х) называется произвольная функция от переменной х, определенная на множестве D, принимающая значения из множества {0,1}.

Множество D, на котором определен предикат Р (х), называется областью определения предиката Р или его универсом. Множество всех элементов х Î D, при которых предикат принимает значение 1 (истина), называется множеством истинности предиката Р (х). Например, предикат - «х - четное число» определен на множестве натуральных чисел N, множеством истинности для него является множество всех четных чисел. Предикат S (х) - «-1£ sin (х) £ 1» определен на множестве действительных чисел R и его множество истинности - R.

Определение 1.2. п - местным предикатом Р (,…, 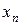) называется функция п переменных , … , 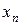определенная на множестве 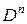= D ´ …´ D,

принимающая значения из множества {0,1}.

Предикат Q (x,y,z): является трехместным предикатом; предикат P (,…, 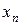): - п - местный.

Выражение Р (,…, 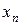) называют элементарной формулой или атомом. Класс формул содержит все элементарные формулы и составные формулы, построенные из элементарных многократным применением всех операции логики высказываний: Ø, Ù, Ú, ® и др. Кроме того вводится две новые операции " («для любого») и $ («для некоторых» или «существует»). Утверждение «для всех х верно P (х)» символически записывается " х P (х). Символ " называется квантором всеобщности. Утверждение " х P (х) истинно, если истинно P (с), какой бы конкретный предмет с из универса предиката P мы ни подставляли вместо х. Например, высказывание " х ( 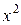³ 0) истинно, если универс - множество действительных чисел. Это высказывание ложно, если универс содержит комплексные числа, т.к. .

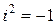Символ $ называется квантором существования. Утверждение «существует такое х, что P (х)» символически записывается $ х P (х). Символ $ называется квантором существования. Высказывание $ х P (х) истинно, если в универсе найдется, хотя бы одно значение с, при котором P (с) истинно.

$ х P (х) ложно, если при любом значении с ложно P (с). Пусть задан предикат Р (х): «число х кратно 3». Тогда на множестве натуральных чисел N высказывание $ х Р (х) истинно, а " х Р (х) - ложно. По старшинству (в отношении расстановки скобок) кванторы имеют самый высокий приоритет. Формула

" х Р ® Q означает (" х Р) ® Q, а не " х (Р ® Q).

Кванторные операции применяются и к многоместным предикатам. В предикатах, зависящих от нескольких переменных, кванторы можно использовать несколько раз. Предикат " x " y " z Q (x,y,z) читается «для каждого x, для каждого y, для каждого z имеет место Q (x,y,z)», этот предикат истинен, когда для любого набора значений x,y,z из универса истинно. Высказывание $ х $ y $ z Q (x,y,z) истинно, если универс для Q содержит, хотя бы один набор значений, для которых .

Предикат " Р (,…, 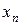) зависит от (п - 1)- переменной в отличие от предиката Р (,…, 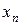), который зависит от п переменных. Истинностное значение предиката " Р (,…, 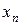) можно установить, если задать значения 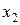, …, , 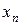п ³ 2. Рассмотрим предикат P (x,y) «х: y - y делитель х», определенный на множестве N. Предикат " х Р (х, y) - «y - делитель любого х» зависит от y и не зависит от х, он истинен для y=1 и ложен для всех остальных значений y. Предикат $ y Р (х, y) - «существует такое y, которое является делителем х» зависит от х и не зависит от y. Он будет истинен для любого значения х. Применение кванторных операций " и $ приводит к восьми возможным высказываниям:

1." y " х Р (х, y) - «для всякого y и для всякого х выполняется: y - делитель х».

2. $ y " х Р (х, y) - «существует y, которое является делителем любого х».

3. " y $ х Р (х, y) - «для всякого y существует х такое, что х делится на y».

4. $ y $ х Р (х, y) - «существует y и существует х, такие, что y - делитель х».

5." х " y Р (х, y) - «для всякого х и для всякого y выполняется: y - делитель х».

6. " х $ y Р (х, y) - «для всякого х существует такое y, что х делится на y».

7. $ х $ y Р (х, y) - «существует х и существует y, такие что y - делитель х».

8. $ х " y Р (х, y)- «существует х такое, что для всякого y выполняется: х делится на y».

Легко видеть, что высказывания 1, 5 и 8 ложные, а высказывания 2, 3, 4, 6 и 7 истинны.

В формуле " х P (х) ($ х P (х)) подформулу P называют областью действия вхождения квантора " х ($ х). Вхождение переменной х в произвольную формулу Ф называют связанным, если х лежит в области действия некоторого вхождения квантора " или $. Если вхождение переменной х в формулу Ф не является связанным, то его называют свободным. Рассмотрим формулу: " х (Р (х) Ù $ х Q (x, z) ®$ y R (х, y)) Ú Q (z, x).

Отметим индексами все вхождения переменных, связанных кванторами. Расставлять индексы нужно начинать изнутри, продвигаясь наружу в соответствии с построением формулы из ее атомов Р (х), Q (x, z), R (х, y), Q (z, x).

" х ₃ (Р (х ₃) Ù $ х ₁ Q (x ₁, z) ®$ y ₂ R (х ₃, y ₂)) Ú Q (z, x).

Вхождения переменных, оставшихся без индексов (два z и одно x), свободны.

Для формулы Ф запись Ф (,…, 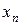) обозначает, что все ее свободные переменные входят в последовательность ,…, .

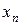Date: 2015-06-06; view: 896; Нарушение авторских прав