Кривая безразличия

Кривая безразличия i показывает все комбинации

апельсинов и яблок, об­ладающие одинаковой полезностью.

Поэтому потребителю безразлично, ка­кую из комбинаций

выбрать. Кривая i имеет отрицательный наклон, так

как уменьшение потребления апельсинов

сопровождается увеличением потреб­ления яблок. Она

является выпуклой, так как ее наклон, выражающий

MRS апельсинов яблоками, уменьшается.

На основании данных, содержащихся в табл. 5-2, построим кри­вую безразличия (рис. 5-3), отложив на осях системы координат количества единиц обоих товаров, входящих в наборы.

КРИВАЯ БЕЗРАЗЛИЧИЯ — это геометрическое

место точек, которое показывает различные

ком­бинации двух благ, обладающих одинаковой

полезностью.

Кривыми безразличия можно заполнить все имеющееся про­странство благ. В этом случае мы получим карту безразличия.

КАРТА БЕЗРАЗЛИЧИЯ — множество кривых

без­различия, каждая из которых представляет

различный уровень полезности.

На рис. 5-4 изображена карта безразличия, содержащая три кривые безразличия. Любая точка, расположенная на более высо­кой по отношению к началу системы координат кривой, предпоч­тительнее, чем точка на более низко расположенной кривой. Так, точка F предпочтительнее, чем точка С, так как представленный ею набор содержит столько же апельсинов, сколько и набор, выражен­ный точкой С, и больше орехов, чем в наборе С. Между тем все наборы, представленные точками на кривой безразличия i имеют ту же полезность, что и набор С.

Легко доказать, что кривые безразличия не пересекаются. Так, если бы кривые i, и i₂ пересеклись в точке, то в этом случае комбинации С, F и D были бы одинаково предпочтитель­ными для потребителя, так как имели бы общую точку, лежа­щую одновременно на обеих этих кривых. Это противоречит очевидному положению о предпочтительности точки F по отношению к точке С.

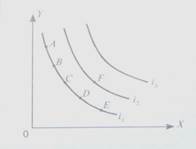Рис. 5-4.

Date: 2015-06-06; view: 555; Нарушение авторских прав