Анализ сезонности

Периодическая и сезонная зависимость (сезонность) представляет собой другой общий тип компонент временного ряда. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i- м элементом ряда и (i – k)-м элементом. Ее можно измерить с помощью автокорреляции (т. е. корреляции между самими членами ряда); k обычно называют лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если ошибка измерения не слишком большая, то сезонность можно определить визуально, рассматривая поведение членов ряда через каждые k временных единиц.

Автокорреляционная коррелограмма. Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 30). На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, так как интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции.

Исследование коррелограмм. При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой. Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т. д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, т. е. после взятия разности с лагом 1).

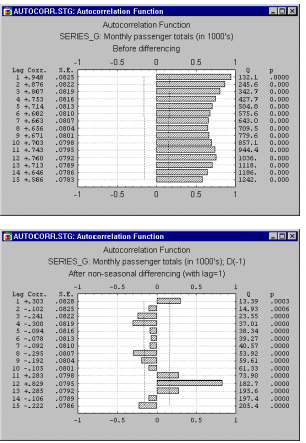
Частные автокорреляции. Другой полезный метод исследования периодичности состоит в исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой углубление понятия обычной автокорреляционной функции. В ЧАКФ устраняется зависимость между промежуточными наблюдениями (наблюдениями внутри лага). Другими словами, частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами. На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна, очевидно, обычной автокорреляции. На самом деле, частная автокорреляция дает более «чистую» картину периодических зависимостей.

Удаление периодической зависимости. Как отмечалось выше, периодическая составляющая для данного лага k может быть удалена взятием разности соответствующего порядка. Это означает, что из каждого i -го элемента ряда вычитается (i – k)-й элемент. Имеются два довода в пользу таких преобразований.

Во-первых, таким образом можно определить скрытые периодические составляющие ряда. Напомним, что автокорреляции на последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций изменит другие автокорреляции, которые, возможно, подавляли их, и сделает некоторые другие сезонные составляющие более заметными.

Во-вторых, удаление сезонных составляющих делает ряд стационарным, что необходимо для применения АРПСС и других методов, например, спектрального анализа.

АРПСС

Процедуры оценки параметров и прогнозирования предполагают, что математическая модель процесса известна. В реальных данных часто нет отчетливо выраженных регулярных составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как необходимо не только выделить регулярные компоненты, но также построить прогноз. Методология АРПСС, разработанная Боксом и Дженкинсом (1976), позволяет это сделать. Данный метод чрезвычайно популярен во многих приложениях, и практика подтвердила его мощность и гибкость. Однако из-за мощности и гибкости, АРПСС – сложный метод. Его не так просто использовать, и требуется большая практика, чтобы овладеть им. Хотя часто он дает удовлетворительные результаты, они зависят от квалификации пользователя.

Два основных процесса

Процесс авторегрессии. Большинство временных рядов содержат элементы, которые последовательно зависят друг от друга. Такую зависимость можно выразить следующим уравнением:

.

Здесь: x – константа (свободный член), f₁, f₂, f₃ – параметры авторегрессии.

Вы видите, что каждое наблюдение есть сумма случайной компоненты (случайное воздействие e) и линейной комбинации предыдущих наблюдений.

Требование стационарности. Заметим, что процесс авторегрессии будет стационарным только, если его параметры лежат в определенном диапазоне. Например, если имеется только один параметр, то он должен находиться в интервале –1< f <+1. В противном случае, предыдущие значения будут накапливаться, и значения последующих могут быть неограниченными, следовательно, ряд не будетстационарным. Если имеется несколько параметров авторегрессии, то можно определить аналогичные условия, обеспечивающие стационарность.

Процесс скользящего среднего. В отличие от процесса авторегрессии, в процессе скользящего среднего каждый элемент ряда подвержен суммарному воздействию предыдущих ошибок. В общем виде это можно записать следующим образом:

Здесь: µ – константа, q₁, q₂, q₃ – параметры скользящего среднего.

Другими словами, текущее наблюдение ряда представляет собой сумму случайной компоненты (случайное воздействие e) в данный момент и линейной комбинации случайных воздействий в предыдущие моменты времени.

Обратимость. Не вдаваясь в детали, отметим, что существует «двойственность» между процессами скользящего среднего и авторегрессии. Это означает, что приведенное выше уравнение скользящего среднего можно переписать (обратить) в виде уравнения авторегрессии (неограниченного порядка), и наоборот. Это так называемое свойство обратимости. Имеются условия, аналогичные приведенным выше условиям стационарности, обеспечивающие обратимость модели.

Date: 2015-11-15; view: 884; Нарушение авторских прав