
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритмы прогнозирования сроков агротехнологических операций
|
|
Разработано множество алгоритмов построения моделей прогнозирования рекомендуемых дат агротехнологических операций на основе корреляционно-регрессионного анализа. На рисунке 2.9 приведены признаки их классификации.


Рисунок 2.9 - Признаки классификации алгоритмов прогнозирования сроков агротехнологических операций
На основе приведенных алгоритмов можно получить модели прогнозирования сроков агротехнологических операций. В зависимости от природно-климатических особенностей территории возделывания, адекватными могут быть однофакторные или многофакторные уравнения регрессии. В однофакторных уравнениях в качестве фактора рассматривают обычно суммы среднесуточных температур воздуха. В многофакторных (двухфакторных) уравнениях в качестве дополнительного фактора наряду с суммой температур используют суммы осадков за предшествующие периоды. При этом в зависимости от исходных данных наибольшей точностью могут обладать как однофакторные так и многофакторные модели.
Для своевременного прогнозирования рекомендуемой даты посева при определении периода суммирования необходимо учитывать некоторую заблаговременность l. При этом для предприятия вполне достаточно 7-10 дней для своевременной и полноценной подготовки к посевным работам.
Согласно рисунку 2.8 периоды суммирования параметров k и заблаговременность l взаимосвязаны: чем больше k тем меньше l, при неизменных T0 и Ti.
В качестве заданной продолжительности периода k могут использоваться фиксированные значения, принятые в агроклиматологии, кратные 10 суткам. Однако не всегда связи, получаемые для этих периодов, являются наилучшими. При этом оптимальная заблаговременность l также может быть разной. Поэтому целесообразно использовать переменные продолжительности периодов оценки параметров k и l. Так, например, на основе данных Иркутска за 1989 – 2011 гг. оптимальная заблаговременность прогноза составила 9 суток. При этом k изменялось от 7 до 24, а l - от 1 до 20 соответственно. Период суммирования показателей тепла и увлажнения составил 1-19 апреля. Расчетная дата посева на 2012 г. - 27 апреля.
Еще одним ключевым показателем при определении периода суммирования k является выбор её начальной даты T0. В ходе анализа выявлено, что при продолжительности периода k более чем 30 суток точность уравнений регрессии (2.2) и (2.3) значительно уменьшается, поэтому рассматривать более продолжительные периоды нецелесообразно. А, так как фактические даты посевов на территории региона в большинстве случаев находятся в первой декаде мая, в расчетах в качестве T0 использовалось 1 апреля, дата на месяц ранее даты большинства фактических посевов. Кроме того, чтобы максимально исключить отрицательные температуры при суммировании и при минимальном изменении периода k, предлагается использовать в качестве T0 – дату перехода среднесуточной температуры воздуха через 0ºС. Например, для Тулуна по данным за 2001-2011 гг. б о льшую точность показало уравнение регрессии с T0 равным дате перехода через 0ºС (16 апреля), чем с T0 равным 1 апреля. Коэффициенты детерминации уравнений составили  =0,47 и
=0,47 и  =0,44, а средние относительные ошибки 26,1% и 28,7% соответственно.
=0,44, а средние относительные ошибки 26,1% и 28,7% соответственно.
Значение при построении уравнений регрессии (2.2)–(2.9) имеет выбор рассматриваемого многолетнего периода M. В зависимости от ее продолжительности, коэффициенты уравнений регрессии могут изменяться, и точность их также может колебаться. При этом необязательно, что при б о льшей продолжительности M, уравнения регрессии должны обладать б о льшей точностью.
Для прогнозирования сроков технологических операций можно использовать, наряду с фактическими данными, прогнозные значения температур и осадков. Достоверность полученных результатов зависит от точности прогнозирования параметров тепла и увлажнения. Так, например, используя прогнозные данные на несколько дней вперед, увеличивается заблаговременность прогноза l в ущерб его точности.
Рассмотрим алгоритм определения сроков посевных операций с оптимальной заблаговременностью l, с заданной продолжительностью многолетнего периода M, без использования прогностических данных на основе многофакторного анализа.
Такой алгоритм позволяет строить модели прогнозирования с предварительным определением оптимальной заблаговременности прогноза при заданном многолетнем периоде. На рисунке 2.10 показана схема этого алгоритма. Обычно в качестве рассматриваемого многолетнего периода используются данные за 10 и более лет.
Согласно алгоритму в начале определяются даты начала и окончания периода суммирования параметров T0 и Tn и даты прогрева почвы Ti, далее поэтапно строятся ряды результативного признака y и факторов x1 и x2 для различных продолжительностей периода k. Затем определяются различные однофакторные и двухфакторные зависимости y от x1, y от x2 или y от x1 и x2, и осуществляется выбор значимых, адекватных и имеющих наибольшую точность моделей, которым соответствует расчетная заблаговременность lопт.

Рисунок 2.10 – Схема определения рекомендуемого срока посевов с оптимальной заблаговременностью
Выбор того или иного аналитического выражения связан с оценкой адекватности модели согласно анализу остатка ряда и точности по коэффициенту детерминации (или средней относительной ошибке аппроксимации). При выявлении детерминированной составляющей остатка ряда осуществляется уточнение модели регрессии и новое уравнение повторно оценивается на адекватность.
Алгоритм реализован для юго-восточного лесостепного (Иркутск, Усолье-Сибирское) и центрального лесостепного (Тулун) агроландшафтных районов региона. В таблице приведены предлагаемые линейные уравнения для всех трех пунктов и полученные прогностические даты прогрева почвы до рекомендуемой температуры на 2012 г. (таблица 2.4).
Таблица 2.4 – Результаты расчета рекомендуемых дат посева на 2012 г.
| Пункт наблюдения | г. Иркутск | г. Усолье-Сибирское | г. Тулун |
| Температура прогрева почвы td | 10ºС | 8ºС | 6ºС |
| Многолетний период M | 1989-2009 | 1987-2011 | 1987-2011 |
| Период суммирования параметров k | 1-19 апреля | 1-21 апреля | 11-20 апреля |
| Оптимальная заблаговременность l | 11 суток | 8 суток | 14 суток |
| Уравнение регрессии | 
| 
| 
|
| Коэффициент детерминации R2 | 0,72 | 0,81 | 0,42 |
| Рекомендуемая дата посева на 2012 г. | 30 апреля | 29 апреля | 4 мая |
| Стандартное отклонение | 2,7 | 2,3 | 2,2 |
| Средняя относительная ошибка аппроксимации, % | 16,8 | 13,2 | 30,1 |
В результате исследования выявлено, что в отличие от Иркутского и Усольского районов для Тулунского района более пригодны двухфакторные модели, однако, точность уравнений регрессии в большинстве случаев невысока (R 2<0,5, Eотн >20%). Для Иркутска уравнения регрессии обладают большей точностью, если в качестве рекомендуемой температуры для посева td использовать 10°C, для Усолье-Сибирского – 8°C, а для Тулуна – 6°C. Полученные значения для всех трех пунктов входят в диапазон температур, пригодных для посева зерновых культур.
При расчете учитывались различные значения периодов суммирования параметров k. Для расчета рекомендуемых дат использовались значимые и адекватные уравнения регрессии с наибольшей точностью согласно коэффициенту детерминации и средней относительной ошибке. Так, при статистической обработке данных г. Иркутск, k изменялось от 7 до 24. На рисунке 2.11 приведены результаты методики выбора.
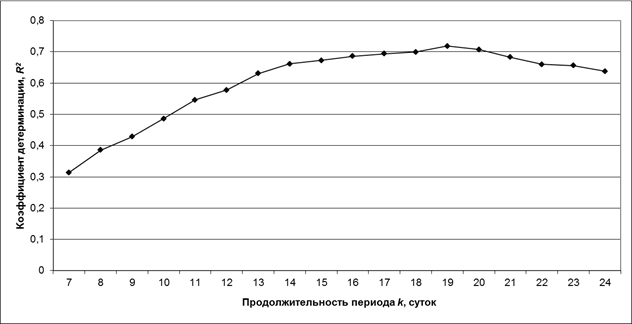

Рисунок 2.11 – Значения коэффициентов детерминации в зависимости от продолжительности периода k
Согласно рисунку 2.11 при увеличении параметра k коэффициент детерминации уравнения сначала растет, достигает максимального значения при k =19 и постепенно уменьшается до R2 =0,64 (при k =24). Коэффициент детерминации значительно ниже при k <13. Поэтому для продолжительности суммирования суточных температур и осадков целесообразно использовать уравнения с k >13. При k =19 уравнение обладает максимальным значением коэффициента детерминации (R2 =0,72) и заблаговременность при этом составит l =6 суток, что вполне приемлемо для подготовки к посеву. Поэтому в качестве оптимального периода k использовалось именно это значение. При этом рекомендуемой датой посева зерновых в г. Иркутск на 2012 г. является 30 апреля. Расчётный период суммирования показателей тепла и увлажнения составил 1-19 апреля. При этом оптимальная заблаговременность прогноза составила 11 суток. Стандартное отклонение составило 2,7, а средняя относительная ошибка аппроксимации - 16,8%.
Рассмотренный выше алгоритм рассчитывает оптимальную заблаговременность прогнозирования l при заданном многолетнем периоде M. В большинстве случаев, при наличии необходимого количества данных, прогноз на основе этого алгоритма точен и обладает достаточным значением заблаговременности. Однако наибольшей точностью могут обладать уравнения регрессии с малым значением заблаговременности l, не достаточным для своевременной подготовки техники и персонала к посеву. В этих случаях, при наличии многолетних данных за достаточно продолжительный период M (более 10 лет), предлагается использовать алгоритм прогнозирования сроков агротехнологических операций с заданной заблаговременностью и с расчетом оптимального многолетнего периода M. Общая схема этого алгоритма приведена на рисунке 2.12.
Согласно алгоритму после построения рядов относительных дат y строится множество уравнений регрессий для различных периодов M, которые постепенно увеличиваются, начиная от минимальной продолжительности, необходимой для построения регрессионной модели (например, M =6), до общей продолжительности, по которой имеются фактические данные. Продолжительность l устанавливается в соответствии с необходимым значением заблаговременности прогноза и остается неизменным. Для дальнейших расчетов используется(-ются) адекватные и значимые модель(-ли) с наибольшим(-ими) коэффициентом детерминации R2.

Рисунок 2.12 – Схема определения рекомендуемых сроков посева с оптимальной продолжительностью периода M
Согласно этому алгоритму по г. Иркутск (рисунок 2.13), выявлено, что уравнения регрессии адекватны и обладают наибольшей точностью при рассматриваемом многолетнем периоде с 1989 по 1997 гг.(M =9), коэффициент детерминации при этом составляет R2 =0,84. Рассматривались многолетние периоды M =8..20, начиная с 1989 по 1996 гг. и заканчивая с 1989 по 2009 гг. Период суммирования k составил 19 суток (с 1 апреля по 19 апреля).

Рисунок 2.13 – Зависимость коэффициента детерминации от многолетнего периода M
Еще одним важным вопросом при расчете рекомендуемых дат посева является выбор критической температуры td. Так, для разных культур и климатических зон используются разные его значения. Интерес вызывает зависимость точности полученных уравнений регрессии от выбранной td.
Проведен анализ точности линейных уравнений регрессий для различных k и td по Иркутску и Усолье-Сибирскому (рисунок 2.14).


а) Иркутск


б) Усолье-Сибирское
Рисунок 2.14 – Значения коэффициентов детерминации в зависимости от продолжительности периода k и критической температуры td
В качестве многолетнего периода M взят период с 1990 по 2009 гг. Продолжительность периода суммирования параметров k менялась от 7 до 24 суток (от 1 – 7 апреля, до 1- 24 апреля). В ходе исследования выявлено, что по данным г. Иркутск наибольшей значением коэффициента детерминации обладают уравнения при td =10ºС (R2 =0,78) и td =12ºС (R2 =0,68). При td =6ºС и 8ºС коэффициент детерминации R2 <0,5. Однако по данным Усолья-Сибирского напротив, наибольшее его значение наблюдалась при td =6ºС и 8ºС (R2 =0,81). При td =10ºС его значение была ниже, а при td =12ºС уравнения показали очень низкое значение (R2 <0,35).
Иркутск и Усолье-Сибирское относятся к одной центральной лесостепной агроландшафтной зоне. Для выявления зависимости точности уравнений регрессии от td в другой климатической зоне использовались данные по Тулуну. Для этого пункта характерна пригодность использования сумм осадков в качестве дополнительного параметра в уравнении регрессии зависимости дат посева от агроклиматических параметров, поэтому осуществлялись как однофакторный, так и двухфакторный линейные анализы (рисунок 2.15).
Проведенный многофакторный анализ по городу Тулун показал, что:
- уравнения не удовлетворяют критериям значимости, адекватности и обладают низкой точностью;
- наибольшую точность имеют уравнения при td =6ºС, а в остальных случаях точность уравнений неудовлетворительна;
- точность однофакторных уравнений выше при б о льших k, а двухфакторных - при меньших.
Таким образом, для Иркутска наибольшей точностью (согласно коэффициенту детерминации) обладают линейные уравнения с рекомендуемой температурой td =10ºС, для Усолья-Сибирского – с td =8ºС, а для Тулуна td =6ºС.
Линейные уравнения регрессии, благодаря универсальности их применения и простоте, широко используются для моделирования производственных параметров. Однако далеко не всегда зависимости этих параметров можно выразить линейными функциями, так как при этом могут возникать неоправданно большие ошибки [28].


а) однофакторный анализ


б) двухфакторный анализ
Рисунок 2.15 – Значения коэффициентов детерминации в зависимости от продолжительности периода k и критической температуры td по Тулуну
Наряду с линейными моделями возможно использование нелинейных функций: полинома, логарифмической, экспоненциальной, степенной и др. Применение нелинейных уравнений может увеличить точность аппроксимации, что положительно скажется на прогнозировании [51].
При использовании некоторых нелинейных уравнений необходимо, чтобы результативный признак и факторы регрессии были положительными.
В качестве одного из факторов в предложенных регрессионных моделях, используется сумма среднесуточных температур воздуха за предшествующий период.
Для большинства рассматриваемых лет по Иркутску, Усолье-Сибирскому и Тулуну эта сумма температур за периоды суммирования k положительна. Однако в годы с холодными весенними периодами возможны их отрицательные значения. Например, в 2006 г. по данным Иркутска сумма температур с 1 по 19 апреля составила -62,7°C.
Для того чтобы исключить отрицательные суммы температур, предлагается при расчете температуры использовать шкалу Фаренгейта (°F).
При этом формула перевода суммы температур по Цельсию в суммы температур по Фаренгейту выглядит следующим образом
 , (2.11)
, (2.11)
где  и
и  - температуры в градусах Фаренгейта и Цельсия соответственно, k – продолжительность периода суммирования температур.
- температуры в градусах Фаренгейта и Цельсия соответственно, k – продолжительность периода суммирования температур.
В работе для аппроксимации однофакторных зависимостей дат посева от суммы температур (данные Иркутска и Усолья-Сибирского) использовались следующие нелинейные функции: полином второй степени, логарифмическая, степенная и экспоненциальная.
При описании двухфакторных зависимостей (данные Тулуна) рассматривались линейное, логарифмическое и полиномиальные выражения в различных вариантах. В качестве дополнительного фактора, помимо суммы среднесуточных температур x 1 воздуха, использовалась сумма суточных осадков x 2.
В качестве температуры td для каждого пункта применялись рекомендуемые значения: для Иркутска это значение 10°C, для Усолья-Сибирского - 8°C, а для Тулуна - 6°C [10].
Для каждого вида функции использовались периоды суммирования параметров, при которых уравнения имели наибольшее значение коэффициента детерминации. На рисунке 2.16 показаны линейные и полиномиальные функции аппроксимации зависимости дат посева от сумм среднесуточных температур воздуха для Иркутска (период k - с 1 по 19 апреля) и Усолья-Сибирского (период k - с 1 по 21 апреля).
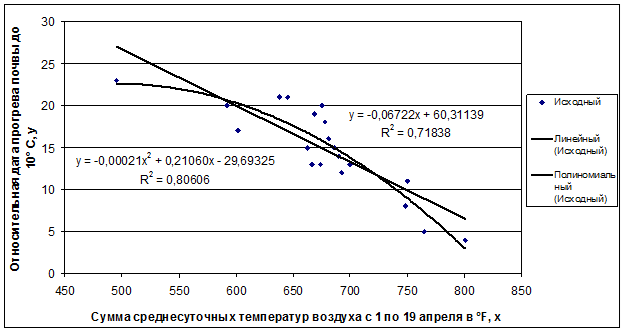
Рисунок 2.16 - Линейная и полиномиальная функции аппроксимации зависимости дат посева от сумм среднесуточных температур воздуха по Иркутску
В таблице 2.5 приведены результаты сравнения точности некоторых линейных и нелинейных уравнений для всех трех пунктов и полученные прогностические даты прогрева почвы до рекомендуемой температуры. Оценка точности моделей производилась по коэффициенту детерминации, стандартной ошибке и средней относительной ошибке аппроксимации.
Согласно таблице 2.5 наибольшей точностью согласно коэффициенту детерминации для Иркутска обладает полиномиальное уравнение, а линейное и логарифмическое имеют меньшую точность, но они также пригодны для прогнозирования. Ввиду больших относительных и абсолютных ошибок степенной и экспоненциальной зависимостей, последние не применимы для прогнозирования.
Таблица 2.5 - Оценка точности линейных и нелинейных уравнений регрессии для Иркутской области
| Показатели | Пункт наблю-дения | Линейная функция | Полиномиальная функция |
| Уравнение регрессии | Иркутск | y=-0,067x+60,3 | y =-0,00018x2 + +0,21x-29,7 |
| Рекомендуемая температура td | 10°C | ||
| Многолетний период | 1989 – 2009 гг. | ||
| Период суммирования параметров | 1-19 апреля | ||
| Коэффициент детерминации | 0,72 | 0,81 | |
| Стандартная ошибка аппроксимации | 2,7 | 2,5 | |
| Средняя относительная погрешность, % | 16,8 | 15,1 | |
| Расчетная дата посева на 2012 г. | 30 апреля | 30 апреля | |
| Фактическая дата посева на 2012 г. | н.д. | ||
| Уравнение регрессии | Усолье-Сибирское | y=-0,071x+66,4 | y=0,00001x2- -0,079x+69,6 |
| Рекомендуемая температура td | 8°C | ||
| Многолетний период | 1987 – 2010 гг. | ||
| Период суммирования параметров | 1-21 апреля | ||
| Коэффициент детерминации | 0,81 | 0,81 | |
| Стандартная ошибка | 2,3 | 2,3 | |
| Средняя относительная погрешность, % | 13,2 | 13,4 | |
| Расчетная дата посева на 2012 г. | 29 апреля | 29 апреля | |
| Фактическая дата посева на 2012 г. | н.д. | ||
| Уравнение регрессии | Тулун | y=-0,048x1+ +0,047x2++40,4 | y=-1,05x12-0,096x22+ +0,00072x1+0,0027x2+ +386 |
| Рекомендуемая температура td | 6°C | ||
| Многолетний период | 1987 – 2008 гг. | ||
| Период суммирования параметров | 11-30 апреля | ||
| Коэффициент детерминации | 0,42 | 0,8 | |
| Стандартная ошибка | 2,2 | 1,3 | |
| Средняя относительная погрешность, % | 30,1 | 15,3 | |
| Расчетная дата посева на 2012 г. | 4 мая | 2 мая | |
| Фактическая дата посева на 2012 г. | 2 мая |
Для Усолья-Сибирского линейная и полиномиальная зависимость имеют практически одинаковую точность. Меньшей точностью обладают логарифмическая функция. Что касается степенной и экспоненциальной зависимости то, как и в предыдущем случае, они не рекомендуются для использования в прогнозировании.
По данным Тулуна полиномиальное уравнение является адекватным, значимым и обладает большим значением коэффициента детерминации по сравнению с линейной зависимостью.
Высокие стандартные и средние относительные ошибки уравнений регрессии по некоторым пунктам связаны с тем, что в разные годы по-разному происходит накопление сумм температур и можно выделить два вида функции: одна – возрастающая, а вторая имеет волнообразный вид.
Расчетные даты посева зерновых на 2012 г. согласно уравнениям с наибольшими точностями (таблица 2.8) составили 30 апреля для Иркутска (дата прогрева почвы до 10°C), 29 апреля для Усолья-Сибирского (дата прогрева почвы до 8°C) и 2 мая для Тулуна (дата прогрева почвы до 6°C).
Отметим, что прогнозная дата посева по полиномиальному уравнению для Тулуна, совпала с фактической датой прогрева до рекомендуемой температуры. К сожалению, поскольку данные о температурах почвы в Иркутске и Усолье-Сибирском отсутствуют, не удалось сравнить даты по этим пунктам.
Таким образом, для Иркутска рекомендуется использовать однофакторные полиномиальные уравнения регрессии, для Усолья-Сибирского однофакторные линейные, а для Тулуна – двухфакторные полиномиальные.
Согласно таблице 1.3 по расчетным датам посева можно определить даты других технологических операций, связанные с обработкой посевов. В таблице 2.6 приведены расчетные даты начала некоторых основных технологических операций по возделыванию пшеницы сорта Тулунская 12 зерновых для трех пунктов на 2012 г.
Таблица 2.6 – Расчетные даты проведения технологических операций по возделыванию пшеницы сорта Тулунская 12 для Иркутской области на 2012 г.
| Операция по технологической карте | Расчетные даты | ||
| Иркутск | Усолье-Сибирское | Тулун | |
| Культивация | 29 апреля | 28 апреля | 1 мая |
| Посев | 30 апреля | 29 апреля | 2 мая |
| Внесение удобрений | 30 апреля | 29 апреля | 2 мая |
| Прикатывание | 1 мая | 30 апреля | 3 мая |
| Боронование до всходов | 5 мая | 4 мая | 7 мая |
| Уборка культуры | 2 августа | 1 августа | 5 августа |
Таким образом, на основе разработанных алгоритмов рассчитаны даты посева, с помощью которых определены даты других основных технологических операций на 2012 г. для Иркутской области.
Date: 2015-11-14; view: 642; Нарушение авторских прав