Робастное H2 оценивание

Рассмотрим следующую неопределенную систему

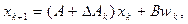
(3.1)

(3.2)

(3.3)

где есть состояние, является белый шум вход с нулевым средним и единичной мощности спектральной плотности, является измерение и это сигнал, чтобы оценивать. и являются параметрами неопределенности, задаются

(3.4)

где 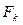является неизвестной матрицы блочно-диагональной формы

diag так же и

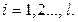
Должно быть ясно, что в приведенной выше модели сигнала, входной шум и измерение шума были так же установлены. Однако, это не теряет общности, так как если входной шум и измерения уровня шума соответственно и 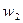мы можем записать и заменить и на и , соответственно. В этой ситуации, заметим, что если и , мы имеем дело с робастной проблемой деконволюции.

В данной статье мы не излагаем стандартные предположения, такие как, что матрица имеет полный ранг строки [14].

Представим оценивание в форме

(3.5)

(3.6)

Как следует из (3.1) ~ (3.3), (3.5) и (3.6), что погрешность оценивания системы является

(3.7)

(3.8)

где и

,

.

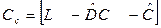В робастной задаче H₂ оценивания находится оценка вида (3.5) и (3.6), так что ошибка системы (3. 7) и (3.8) асимптотически устойчива и удовлетворяет ошибке ковариационного оценивания для некоторой матрицы

(3.9)

для всех допустимых неопределенностей. Кроме того, критерий качества, trace , должен быть сведен к минимуму.

Заметим, что при (3.6) устанавливается равным нулю, оценки (3.5) и (3.6) будут одношаговыми перед предиктором, который был изучен в [5].

Следующий результат дает решение LMI для вышеуказанной робастной задачи H₂ оценивания.

Теорема 3.1 Предположим, что система (3.1) квадратично устойчива. Следовательно, всегда будет существовать устойчивая H₂ оценка вида (3.5) и (3.6). Кроме того, робастность H₂ оценивания может быть получена путем решения следующей оптимизации.

trace 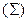(3.10)

при условии

(3.11)

(3.12)

где обозначает запись, которая может быть выведена из собственности симметрии матрицы

diag

являются матричными масштабирования 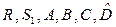матрицы, подлежащие определению.

Действительно, с учетом оптимальных решений 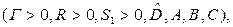робастное H₂ оценивание может быть вычислено с помощью

(3.13)

(3.14)

(3.15)

(3.16)

Доказательство Во-первых, это известно из [5], что робастное H₂ оценивание всегда существует, пока система является квадратично устойчивой.

Далее, применяя лемму 2.2 (а) к системе ошибок (3.7) и (3.8),робастный H₂ критерий качества оценивания может быть получено trace 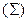с учетом

где является блочно-диагональной матрицей масштабирования.

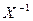Разложим и на

Также обозначим

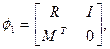
и введем замену переменных следующим образом:

(3.17)

(3.18)

(3.19)

Тогда, до- и после- умножения и соответственно diag diag 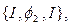их транспонируем и вводим замену переменных в (3.17) - (3.19) тем самым получая робастное оптимальное оценивание может быть преобразовано в оптимизацию задачи:

trace 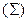(3.20)

при условии

(3.21)

(3.22)

Далее, до- и после- умножения по diag и полагая, что , (3.11) следующим образом. Точно так же, до- и после- умножения 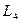по diag и применяя дополнение Schur, могут быть получены (3.11) и (3.12). Кроме того, легко заметить, что (3.14) ~(3.16) следует, определить

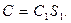
Замечание 3.1 Робастный H₂ одношаговый прогноз проблемы для систем с единой неопределенностью блока был изучен в [4 - 6], где их решение заключается в поиске такого параметра масштабирования, с которым связанные разностные уравнения Риккати разрешимы. Это трудно, особенно в том случае, когда задана неопределенность нескольких блоков и участвуют несколько параметров масштабирования.