Робастный H2 анализ

Рассмотрим устойчивую дискретную LT1 систему в форме пространственного уравнения:

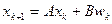, (2.1)

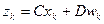, (2.2)

где 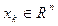является состоянием, 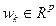является входным и 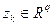является выходным 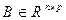, 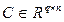и 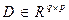постоянные матрицы.

Передаточная функция системы имеет вид

,

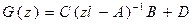и его H₂ норма определяется как

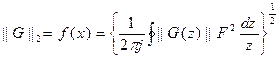, (2.3)

Замечание 2.1 Для линейных стационарных систем (2.1) и (2.2), H₂ норма имеет следующие эквивалентности:

Пусть на выходе соответствует входу 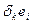, где 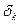символ Кронекера Дельта и 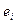является столбцом 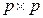единичной матрицы. Затем

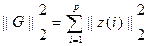
1) Предположим, что является белый шум с нулевым средним и единичной мощности спектральной плотности. Затем

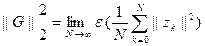
где математическое ожидание.

Хорошо известно, что H₂ норма может быть оценена через управляемость и наблюдаемости грамианов:

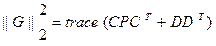
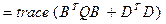
(2.4)

где управляемость грамиан P и наблюдаемость грамиан Q являются единственными решениями в уравнении Ляпунова:

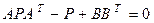, (2.5)

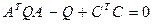, (2.6)

соответственно.

H₂ норма также может быть вычислена по следующей оптимизации [11].

Лемма 2.1 оптимальное решение

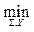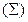trace (2.7)

при условии

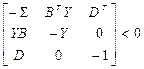, (2.8)

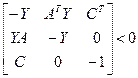, (2.9)

c 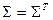и 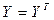таково, что

.

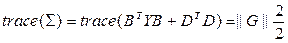Когда существует неопределенность параметров, система (2.1) и (2.2) читается

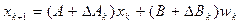, (2.10)

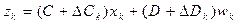, (2.11)

где, 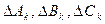и 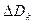представляют изменяющиеся во времени неопределенные параметры, которые являются структурой

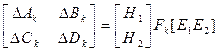, (2.12)

в то время как неизвестная матрица в блочно-диагональной форме

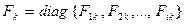с и 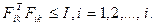(2.13)

Предположение, что представляет собой квадратичную матрицу производится только для простоты изложения.

Для неопределенной системы (2.10) и (2.11), мы вводим понятие квадратичной устойчивости [12]:

Date: 2015-11-14; view: 316; Нарушение авторских прав