
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

О маятнике
|
|
| Тело, падающее вдоль хорд окружности, проходит их за такое же время, как если бы оно проходило весь диаметр |
Начертим несколько наклонных плоскостей между точкой А и горизонтальной линией ВС и опустим перпендикуляры из С на эти плоскости. Наметим центр на равных расстояниях от А и от С и начертим окружность по угловым точкам D, Е, F. Линии AD, АЕ, AF (рис. 25) — хорды окружности; и мы
можем во второй полуокружности начертить прямые, которые, будучи параллельны первым, будут им равны и одинаково наклонны.
Ведь очевидно, что все эти прямые играют ту же роль, что и плоскости, о которых мы только что говорили. Тело спустится вдоль каждой из них за такое же время, как если бы оно падало с верха диаметра вниз из А в С.
Сколько бы мы ни проводили хорд в вертикально поставленной окружности, тело всегда затратит одинаковое время на прохождение каждой хорды, и время это будет равно тому, которое оно затратило бы на прохождение диаметра. Вы также заметите, что хорды пропорционально степени их наклона будут более длинными или более короткими.
| Маятник производит колебания за то же время, за какое он прошел бы четыре диаметра окружности, радиусом которой он является |
Сила тяготения всегда действует перпендикулярно, и независимо от угла наклона плоскости тело, достигнув горизонтальной линии ВС, имеет ту же силу, как если бы оно падало перпендикулярно из А в С. Пусть тело подвешено (рис. 25) к центру М на нити, длина которой равна полудиаметру

окружности. Это тело, опускаясь из h, не может упасть ниже С; но сила, приобретенная им при прохождении данного пути, может быть использована для прохождения еще одного, равного ему пути, и оно вновь поднимется в F. Дойдя до этой точки, оно утратит всю свою силу и, таким образом, вновь упадет под действием своего тяготения, вновь обретет достаточную силу, для того чтобы
подняться в точку h, откуда оно снова упадет, и т. д.
Тело, подвешенное таким образом, называется маятником. Оно может быть подвешено на веревке либо на проволоке. Движение маятника из h в С и из С в h называется колебанием или качанием.
Оно падает ускоренным движением из h в С за то же время, за какое оно упало бы из А; и за такое же время оно поднимается в F затухающим движением.
Стало быть, если бы за эти два промежутка времени оно падало перпендикулярно из точки А, оно прошло бы четыре диаметра окружности.
Значит, тело, подвешенное в центре М, затратило бы на колебание такое же время, какое оно затратило бы, проходя перпендикулярно четыре диаметра, либо, что то же самое, проходя высоту маятника восемь раз.
| Условия, необходимые для изохронных колебаний |
Таково соотношение между движением колебательным и движением перпендикулярным, когда, по нашему предположению, маятник опускается и поднимается по хордам. Ведь поскольку дуги окружности тем менее отличаются от хорд, чем они меньше, предполагается, что соотношение остается тем же, когда маятник совершает колебание по малой дуге LCK. По правде говоря, это допущение не совсем точно, поскольку геометры доказывают, что время, необходимое для того, чтобы опустить тяжелое тело по бесконечно малой дуге, относится к времени, необходимому для того, чтобы опустить его по хорде той же дуги, как длина окружности — к четырем ее диаметрам, или приблизительно как 355 к 452. Между тем периоды колебания по сколь угодно малым дугам окружности равны, потому что они соотносятся как равные периоды падения по хордам этих дуг. Вам следует отметить, что во всем сказанном нами о движении мы упускаем из виду трение, а также сопротивление воздуха. Но трение тем менее ощутимо, чем длиннее маятник и чем меньшую дугу он описывает.
Если бы не существовало ни трения, ни сопротивления воздуха, маятник, раз качнувшись, вечно продолжал бы свои колебания в равные промежутки времени. Когда маятник короток, а дуги большие и трение и сопротивление воздуха более ощутимы, то колебания происходят в неравные промежутки времени. А когда, наоборот, маятник длиннее, а дуги меньше, колебания могут без ощутимой ошибки рассматриваться как происходящие в одинаковые периоды
времени, до тех пор пока маятник не остановится. Подобные колебания называются изохронными.
| Соотношение между длиной маятника и продолжительностью колебаний |
Время колебаний тем меньше, чем короче сам маятник. Вот каково должно быть это соотношение (рис. 26). AGBE и D/Bi — две окружности, диаметры которых АВ и DB относятся друг к другу как 4 к 1.

|
Мы доказали, что если тело падает из А в В за определенное время, то за промежуток времени, вдвое меньший,

оно может упасть лишь из D в В. Мы доказали также, что тело падает вдоль хорды окружности за то время, за какое оно падает вдоль диаметра. Стало быть, тело в Е упадет вдоль хорды BE за время, вдвое большее по сравнению с тем временем, в течение которого тело в f упадет вдоль хорды fВ. Итак, доказано, что если допустить, что дуги BE и fВ подобны или очень малы, то периоды падений по этим дугам, или периоды полуколебаний, соотносятся как периоды падений по хордам. Следовательно, время колебания маятника СВ будет вдвое больше, нежели время колебания маятника Be.
Если Вы хотите, чтобы колебания были в два раза медленнее, надо, чтобы маятник был в четыре раза длиннее, и, напротив, надо, чтобы он стал в четыре раза короче, если Вы желаете, чтобы колебания стали вдвое быстрее.
| Для определения длины маятника необходимо знать центр колебаний |
Но для того чтобы вымерить маятник, надо уметь определить центр колебаний, ведь длина маятника равна расстоянию от центра колебаний до центра подвешивания. Это один из труднейших вопросов. Всего того, что мы изучили до сих пор, недостаточно, чтобы научиться отыскивать точку, которая и есть центр колебания. Ограничимся же тем, что составим понятие о данной проблеме.
Представим себе маятник СР (рис. 27) как рычаг, имеющий точку опоры в центре подвеса С, и, не учитывая силы тяготения рычагов, предположим, что вся тяжесть подвешенного тела сосредоточена в точке Р.
Предположим, что это тело упадет из Р в В со скоростью, пропорциональной массе, умноженной на расстояние от центра тяжести до центра подвеса С, и центр колебания будет тот же, что и центр тяжести. Если предположить то же относительно маятника ср, составляющего лишь одну четверть СР, центр колебания будет для него снова тот же, что и центр тяжести подвешенного тела. Итак, если эти два маятника совершают колебания по дугам, соотносящимся как окружности, частями которых они являются, то р достигнет /, когда Р будет еще только в В; и р возвратится в точку, откуда оно вышло, когда Р достигнет F; р делает два колебания, в то время как Р делает одно, и если р затрачивает полсекунды на каждое колебание, то Р затратит на каждое колебание целую секунду.
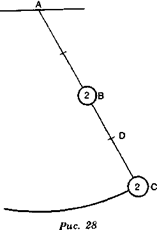
Вы также можете рассматривать (рис. 28) подвешенный рычаг АС, не учитывая силы тяготения, и, разделив его на четыре равные части, поместить на втором делении тело В весом в два ливра, а на конце — тело С весом тоже в два ливра.
Скорости В и С соотносятся как произведения их масс на их расстояние от А, и произведения будут 12. А ведь произведение массы на расстояние для тела весом в четыре ливра, помещенное в D, на третьем делении было бы тоже 12. Следовательно, колебания этого маятника будут происходить со скоростью, составляющей среднее арифметическое по отношению к скоростям В и С, как если бы вся тяжесть сосредоточивалась в D.
Из всех этих предположений Вам ясно, что, чем меньшую тяжесть будет иметь нить по отношению к весу маятника, тем меньше поправок внесет сила тяготения рычага. Так именно и получается, когда тело значительного веса

|
подвешивают на очень тонкую стальную проволоку; наблюдали, что маятник длиной 39,2 дюйма (в английской мере) от центра диска до точки подвеса совершает одно колебание в секунду и, следовательно, 3600 колебаний в час. Этот опыт был проведен с маятником весом 50 ливров, которому была придана чечсвицеобразная форма, чтобы уменьшить
сопротивление воздуха; колебания продолжались целый день. Опыт (рис. 29) приблизительно показывает центр колебания бруска, однородного и имеющего одну и ту же плотность во всех своих частях, так как его колебания изохронны с колебаниями маятника, длина которого была бы равна третям длины бруска.
| Предмет следующей книги |
Я не склонен входить в дальнейшие подробности устройства механизмов. Принципов, изложенных мною, достаточно для объяснения того, как очевидность факта и очевидность разума содействуют друг другу при достижении истины, и, поскольку эти принципы позволяют составить идею о системе планет, я дам Вам представление об этой системе в качестве нового примера рассуждений, касающихся одновременно и очевидности факта, и очевидности разума. Вы увидите, монсеньер, что вселенная — не что иное, как машина, подобная только что изученным нами; это — весы. Эта истина будет доказана Вам при помощи ряда теорем, тождественных теоремам второй книги.
КНИГА ТРЕТЬЯ
Date: 2015-11-13; view: 408; Нарушение авторских прав