Методические указания к решению задач. Задача 1. В цепь синусоидального тока напряжением U = 100 В и частотой f = 50 Гц включена катушка с активным сопротивлением R = 4 Ом и индуктивным XL = 5

Задача 1. В цепь синусоидального тока напряжением U = 100 В и частотой f = 50 Гц включена катушка с активным сопротивлением R = 4 Ом и индуктивным X_L = 5 Ом.

Определить: Ток в катушке; коэффициент мощности; полную, активную и реактивную мощности; емкость, при которой в цепи наступит резонанс токов; построить векторную диаграмму.

Рис.2.1

Решение.

1. Определяем полное сопротивление индуктивной катушки:

Z= = = 6,4 Ом.

2. Ток в катушке определяем по закону Ома: I= U/Z = 100/6,4= 15,6 А.

3. Определяем коэффициент мощности: соsj = R/Z = 4/6,4 = 0,625

4. Угол сдвига фаз между током I и напряжением U:

j = arcсоs R/Z = arcсоs 4/6,4 = arcсоs 0,625 = 51^о.

5. Полная мощность S = UI = 100×15,6 = 1560 ВА.

6. Активная мощность Р = UI соsj =100×15,6 ×0,625 = 975 Вт.

7. Реактивная мощность Q= UI sinj = 100×15,6 ×0,78 = 1217,5 ВАр.

8. Резонанс токов происходит в цепях с параллельным соединением индуктивной катушки и емкости при условии равенства их реактивных проводимостей b_L = b_C. Определим реактивную проводимость индуктивной катушки по формуле:

b_L = X_L/Z² = 5/6,4² = 0,122 См.

Так как проводимость емкости равна b_C = 1/Х_С = = wС, то емкость конденсатора, при которой произойдет резонанс токов, равна:

С = b_C/w = b_C/2pf = 0,122/2×3,14×50 = 0,0003885Ф = 388,5 мкФ.

9. Для построения векторной диаграммы определим напряжения на активном и реактивном сопротивлениях:

U_R = IR = 15,6×4 = 62,4 В, U_L = IX_L = 15,6×5 = 78 В.

Выбираем масштаб: по току m_I = 2 A/см, по напряжению m_U = 10 В/см.

При построении векторной диаграммы первым строим вектор тока, так как он является общим при последовательном соединении элементов цепи. По направлению этого вектора строим вектор напряжения на активном сопротивлении. Под углом 90^о в сторону опережения строим вектор напряжения на индуктивности. Сумма векторов U_R и U_L дает вектор тока в начале электрической цепи U (рис.2.2).

Рис.2.2. Векторная диаграмма

Задача 2.Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Начертить схему цепи и определить следующие величины, относящиеся к данной цепи: полное сопротивление Z; напряжение U, приложенное к цепи; ток I; угол сдвига фаз j (по величине и знаку); активную Р, реактивную Q и полную S мощности цепи. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. Пояснить характер изменения (увеличится, уменьшится, останется без изменения) тока, активной и реактивной мощности в цепи при увеличении частоты тока в два раза. Напряжение, приложенное к цепи, считать неизменным.

Рис.2.3. Электрическая схема

Дано: R₁ = 12 Ом, X_L1 = 4 Ом, X_С1 = 12 Ом, X_С2 = 8 Ом, I = 4 А.

Решение:

Полное сопротивление цепи:

Z = = = 20 Ом

Напряжение, приложенное к цепи:

U = I×Z = 4×20 = 80 В.

Угол сдвига фаз:

j = аrctg 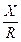= аrctg = аrctg = -53^о

Коэффициент мощности: соsj = соs53^о = 0,6

Определяем активную мощность цепи:

Р = I²R₁ = 4²×12 = 192 Вт. или Р = UIcоsj = 80×4×0,6 = 192 Вт.

Определяем реактивную мощность цепи:

Q = UIsinj = 80×4×(-0,8) = -256 вар.

Определяем полную мощность цепи:

S = = = 320 ВА или S = UI = 80×4 = 320 ВА.

Определяем падения напряжения на сопротивлениях цепи:

U_R1= IR₁ = 4×12 = 48 В; U_L1 = IX_L1 = 4×4 = 16 В; U_C1= IX_C1 = 4×12 = 48 В;

U_C2 = IX_C2 = 4×8 = 32 В.

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току m_I = 0,5 А/см, по напряжению m_U = 10 В/см. Длины векторов согласно выбранного масштаба: _I = 8cм; _U = 8 cм; _UR = 4,8 cм; _UL = 1,6 cм; _UC1 = 4,8 cм; _UC2 = 3,2 cм. Построение векторной диаграммы начинаем с вектора тока, который откладываем по горизонтали. Вектор падения напряжения на активном сопротивлении совпадает по фазе с вектором тока. Из конца этого вектора откладываем в сторону опережения на 90^о вектор напряжения на индуктивной катушке, а в сторону отставания на 90^о откладываем вектор напряжения на первом конденсаторе и к нему прибавляем вектор напряжения второго конденсатора. Геометрическая сумма векторов напряжений U_R, U_L, U_C равна напряжению U, приложенному к цепи.

Рис.2.4. Векторная диаграмма

При увеличении частоты тока в два раза сопротивление индуктивного элемента цепи увеличится в два раза, а емкостных элементов уменьшится в два раза, так как X_L = wL = 2pfL и X_C = 1/wC = 1/2pfC, где f - частота тока. Реактивное сопротивление цепи X = X_L - X_С = 8-10 = 2 Ом уменьшится, следовательно уменьшится полное сопротивление цепи, а ток в цепи при неизменном напряжении увеличится. Так как ток увеличится, то активная мощность Р = I²R₁ также увеличится. Так как реактивное сопротивление при увеличении частоты тока уменьшится, то реактивная мощность Q = I²Х также уменьшится.

Задача 3. Напряжение на зажимах цепи, изображенной на рис. 2.5, изменяется по закону u = U_m sinwt. Амплитудное значение напряжение U_m, значения активных сопротивлений R₁ и R₂, индуктивностей катушек L₁ и L₂, емкостей конденсаторов С₁ и С₂.

Частота питающего напряжения f= 50 Гц.

Необходимо:

1. Определить показания приборов, указанных на схеме (см. рис.2.5).

2. Определить закон изменения тока в цепи.

3. Определить закон изменения напряжения между точками, к которым подключен вольтметр.

4. Определить активную, реактивную и полную мощности источника, активную, реактивную и полную мощности приемников. Составить и оценить баланс мощностей. Рассчитать коэффициент мощности.

5. Определить характер (индуктивность, емкость) и параметры элемента, который должен быть включен в электрическую цепь для того, чтобы в ней имел резонанс напряжений.

Дано. U_m = 240 В, R₁ = 10 Ом, R₂ = 12 Ом, L₁ = 0,01 Гн, С₂ = 800 мкФ.

Рис.2.5. Электрическая схема

Решение.

Определим полное сопротивление электрической цепи.

Для этого необходимо определить реактивные сопротивления индуктивной катушки и конденсатора:

Х_L1 = wL₁ = 2pfL₁ = 2×3,14×50×0,01 = 3,14 Ом.

Х_С2 = 1/wС₂ = 1/2pfС₂ = 1/(2×3,14×50×800×10^-6) = 4 Ом.

Полное сопротивление: Z= = = 22,02 Ом.

Действующее значение U входного напряжения:

U = U_m/ 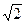= 0,707 U_m = 0,707×240 = 170 В.

Ток в цепи определим по закону Ома: I = U/Z = 170/22,02 = 7,72 А.

Угол сдвига фаз между напряжением U и током I:

j = arctg = arctg = -2,2^o

Активная мощность приемников, показываемая ваттметром:

Р = (R₁+R₂)I² = 22×7,72² = 1311,2 Вт.

Напряжение на конденсаторе показываемое вольтметром:

U_C2 = x_C2I = 4×7,72 = 30,88 В.

Для записи закона изменения тока в цепи найдем его амплитудное значение:

I_m = I 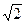= 1,41×7,72 = 10,9 А,

тогда закон изменения тока в цепи:

i = I_msin(wt+j) = 10,9 sin(314t+2,2^o).

Закон изменения напряжения на конденсаторе U_С2:

u_C2 = U_mC2 sin(wt-j) = U_C2 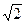sin(wt-j) = 30,88×1,41×sin(314t-90^o) = 43,5×sin(314t-90^o).

Полная мощность источника: S_ист = UI= 170×7,72 = 1312,4 ВА

Активная мощность источника:

Р_ист = UIcosj = 170×7,72×cos2,2^o = 1311,4 Вт.

Реактивная мощность источника:

Q_ист= UIsinj= 170×7,72×sin2,2^o=-50,4 ВАр.

Активная мощность приемников: Р_пр =rI² = 1311,2 Вт.

Реактивная мощность приемников:

Q_пр = Q_L1 - Q_C1 = x_L1I² - x_C2I² = 3,14×7,72² - 4×7,72² = -51,2 ВАр.

Полная мощность приемников:

S_пр = = = 1312,2 ВА.

Баланс мощностей источника и приемников электрической энергии:

S_ист = 1312,4» S_пр = 1312,2 ВА. Р_ист = 1311,4» Р_пр = 1311,2 Вт.

Q_ист = -50,4» Q_пр = -51,2 ВАр.

Коэффициент мощности: cosj = Р_пр/S_пр = 1311,2/1312,2 = 0,999.

Резонанс напряжений имеет место в последовательной цепи R, L, C в том случае, если общее реактивное сопротивление цепи равно нулю, т.е. при X_L = -X_C. Для получения резонанса напряжений в цепь необходимо добавить индуктивную катушку с сопротивлением равным

X_L1 - X_C2 = 3,14 – 4 = 0,86 Ом. Индуктивность такой катушки будет равна: X_L2 = wL₂, отсюда L₂= X_L2/w = 0,86/314 = 0,0027 Гн.

Задача 4.Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), образующие две параллельные ветви. Схема цепи приведена на рис.2.6. Индекс «1» у дополнительного параметра означает, что он относится к первой ветви; индекс «2»- ко второй.

Начертить схему цепи и определить следующие величины: токи I₁ и I₂ в обоих ветвях; ток I в неразветвленной части цепи; напряжение U, приложенное к цепи; активную Р, реактивную Q и полную S мощности для всей цепи. Начертить в масштабе векторную диаграмму цепи.

Каким образом в заданной цепи можно получить резонанс токов? Если цепь не позволяет достигнуть резонанса токов, то пояснить, какой элемент надо дополнительно включить в цепь для этого. Начертить схему такой цепи.

Дано: R₁ = 2 Ом, R₂ = 2 Ом, X_L2 = 3 Ом, Р₂ = 16 Вт.

а) б)

Рис.2.6. Параллельное соединение ветвей

Решение.

Полное сопротивление второй ветви:

Z₂ = = 5 Ом.

Активная проводимость второй ветви: q₂ = = = 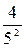0,16 См.

Реактивная проводимость второй ветви: b₂ = = = 0,12 См

Угол сдвига фаз второй ветви: j₂ = аrccos = аrccos 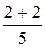= 37^o

Коэффициент мощности: соs j₂ = = = 0,8

Ток второй ветви определим из формулы Р₂ = I₂²R₂:

I₂ = = = 2 А.

Напряжение U, приложенное к цепи: U = Р/Icosj = 16/2×0,8 = 10 В.

Ток первой ветви: I₁ = U/R₁ = 10/2 = 5 А.

Активный ток второй ветви: I_a2 = I₂ cosj₂ = 2×0,8 = 1,6 А.

Реактивный ток второй ветви: I_р2 = I₂ sinj₂ = 2× sin37^o = 2×0,6 = 1,2 А.

Ток I в неразветвленной части цепи:

I = = = 6,7 А.

Активная мощность первой ветви: Р₁ = R₁I₁² = 2×5² = 50 Вт.

Реактивная мощность второй ветви: Q₂ = X_L2I₂² = 3×2² = 12 ВАр.

Полная мощность электрической цепи:

S = = = 67 ВА

Или S = UI = 10×6,7 = 67 ВА.

В электрической цепи с параллельными ветвями можно получить резонанс токов при условии равенства реактивных проводимостей в первой и второй ветвях, содержащих в одной ветви индуктивную катушку, а в другой конденсатор. Для получения резонанса токов в заданной электрической схеме необходимо в первой ветви добавить конденсатор, согласно рис.2.6 (б).

Для построения векторной диаграммы выбираем масштаб: по току

m_I = 1 A/см, по напряжению m_U = 1 В/см.

Первым строим вектор напряжения, так как он является общим для параллельных ветвей. По направлению этого вектора откладываем вектор тока первой ветви I₁. Под углом 37^о в сторону отставания от напряжения строим вектор тока второй ветви I₂, который получается сложением векторов активного и реактивного токов второй ветви. Сложение векторов тока первой и второй ветви дают вектор тока в неразветвленном участке цепи I.

Рис.2.7. Векторная диаграмма

Date: 2015-11-13; view: 17373; Нарушение авторских прав