Анализ сложных цепей постоянного тока

Для электрической цепи, изображенной на рис. 1.2, выполнить следующее:

1.Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа (указав, для каких узлов и контуров эти уравнения записаны). Решать эту систему уравнений не следует.

2.Определить токи в ветвях методом контурных токов.

3. Определить режимы работы активных элементов и составить баланс мощностей.

4. Проверку правильного решения задачи провести по второму закону Кирхгофа.

Дано: Е₁ = 130 В, Е₂ = 110 В, R₁ = 15 Ом, R₂ = 11 Ом, R₃ = 19 Ом,

R₄ = 14 Ом, R₅ = 21 Ом, R₆ = 16 Ом.

Рис.1.2. Сложная электрическая цепь

Схема содержит шесть ветвей, следовательно, имеет шесть неизвестных тока. Выбираем условно положительные направления токов (на схеме указаны стрелками) для которых по законам Кирхгофа необходимо составить шесть уравнений. Число узлов в схеме четыре, поэтому по первому закону Кирхгофа необходимо составить три уравнения:

-I₁ – I₂ + I₃ = 0 для узла (а) (1)

I₁ – I₄ – I₆ = 0 для узла (с) (2)

-I₂ +I₅ + I₆ = 0 для узла (d) (3)

Для составления недостающих двух уравнений разбиваем схему на три независимых контура. Обход контуров проводим против движения часовой стрелки и составляем для каждого из них уравнение, пользуясь вторым законом Кирхгофа:

E₁ = R₁ I₁ + R₄I₄ – R₃I₃ для первого контура (4)

E₂ = R₂I₂ + R₃I₃ + R₅I₅ для второго контура (5)

-R₄I₄ – R₅I₅ + R₆I₆ = 0 для третьего контура (6)

В этих уравнениях все ЭДС и токи, совпадающие с направлением обхода контура, записываются со знаком плюс; ЭДС и токи, направленные навстречу обходу - со знаком минус. Как видно из данного примера, общее число уравнений, составленных по первому и второму законам Кирхгофа, равно числу неизвестных токов, т.е. числу ветвей.

2. Приписываем каждому независимому контуру свой контурный ток: I₁₁, I₂₂, и выбираем произвольное направление каждого из них (см. рис. 1.2). Удобно выбирать направление контурных токов во всех контурах единообразно - по часовой стрелке или против, а направления обхода контуров — по контурным токам.

Составляем уравнения по второму закону Кирхгофа для каждого контура

(7)

Подставляя численные значения ЭДС, источника тока и сопротивлений, получим:

(8)

Полученная система уравнений рассчитывается по методу Крамара:

I₁₁ = , I₂₂ = (9)

где D - определитель системы уравнений (8).

Решим систему трех уравнений первой степени с тремя неизвестными. Соответствующие определители D₁₁, D₂₂,получаемые из Dпутем замены первого, второго и третьего столбцов столбцом свободных членов, равны

= = 48∙51×51 + (-14)×(-19)×(-21) + (-14)×(-19)×(-21) –

(-14)×51×(-14) - 48×(-21)×(-21) - 51×(-19)×(-19) = 124848 – 5586 – 5586 - 9996 – 21168 – 18411 = 64101

∆_I = = 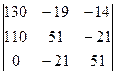130∙51×51 + (-14)×110×(-21) + 0×(-19)×(-21) –

(-14)×51×0 - 130×(-21)×(-21) - 51×(-19)×110 = 338130 + 32340 + 0 + 0 – 57330 + 106590 = 419730

∆_I = = 48∙110×51 + (-14)×(-19)×0 + (-14)×130×(-21) –

(-14)×110×(-14) - 48×0×(-21) - 51×(-19)×130 = 269280 + 0 + 38220 - 21560 + 0 + 125970 = 411910

∆_I = = 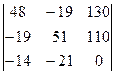48∙0×51 + (-14)×(-19)×110 + (-19)×130×(-21) –

130×51×(-14) - 48×110×(-21) - 0×(-19)×(-19) = 0 + 29260 + 51870 + 92820 + 110880 - 0 = 284830

Воспользуемся формулами Крамара и определим контурные токи:

I₁₁ = = = 6,55 А.

I₂₂ = = = 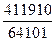6,43 А.

I₃₃ = = = 4,44 А.

4. Значения токов в ветвях находятся как алгебраическая сумма соответствующих контурных токов. Например, ток I₃ в смежной ветви совпадает по направлению с I₂₂ и направлен навстречу I₁₁, поэтому

I₃ = I₂₂ – I₁₁= 6,44 – 6,55 = - 0,12 А

I₄ = I₁₁ – I₃₃= 6,55 – 4,44 = 2,11 А

I₅ = I₂₂ – I₃₃= 6,43 – 4,44 = 1,99 ≈ 2,0 А

5. Ток I₁ в несимметричной ветви (по внешней ветви) равен контурному току I₁₁, поэтому: I₁ = I₁₁ = 6,55 А, соответственно I₂ = I₂₂ = 6,43 А.

I₆ = I₃₃ = 4,44 А.

Метод контурных токов позволяет уменьшить число уравнений, необходимых для решения задачи до числа независимых контуров.

Составим баланс мощностей:

Е₁∙I₁ + Е₂∙I₂ = R₁I₁² + R₂ I₂² + R₃ I₃² + R₄I₄² + R₅ I₅² + R₆ I₆²

130∙6,55 + 110∙6,43 = 15∙6,55² + 11∙6,43² + 19∙0,12² + 14∙2,11² + 21∙2² + 16∙4,44²

851,5 + 707,3 = 643,5 + 454,8 + 0,3 + 62,3 + 84 + 315,4

1558,8 Вт = 1560,4. Вт.

Погрешность расчетов составляет 0,1%, следовательно, задача решена, верно. Проводим проверку правильности решения задачи по второму закону Кирхгофа для первого контура:

E₁ = R₁ I₁ + R₄I₄ - R₃I₃

130 = 15∙6,55 + 14∙2,11 + 19∙0,12

130 = 98,25 + 29,54 + 2,28

130 В = 130,07 В.

Контрольное задание выполнено.

Date: 2015-11-13; view: 1834; Нарушение авторских прав