
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Topic: Principle of inclusion and exclusion
|
|
Example that explains the problem.
In a scientific research institution there are 67 research fellows. 47 fellows know English, 35 persons know German and 23 fellows know both languages. Question: How many research fellows of the institution do not know both languages: English and German?


The set of research fellows is partitioned into such disjoint subsets:
- Those who know both English and German: 23 persons;
- Those who know only English: 47−23 = 24 persons;
- Those who know only German: 35−23 = 12 persons;
The total number of people who knows English and/or German is as follows: 23+24+12 = 59 people. The total number of those who does not know both languages: 67−59 = 8 people.
The above answer can be written in such a way: 8 = 67−23−24−12 = 67−23−(47−23) −(35−23) = 67−47−35+23.
Now we see the pattern (the regularity): from the general number of the staff subtract the number of those who know English and subtract the number of German speakers. By doing so we include some people in two lists: the list of English speakers and the list of German speakers.
These people who know both languages are subtracted 2 times.
Adding this number, we obtain the number of people who do not know any of these 2 languages.
Let us state the problem in a general case:
Given N objects. Each of them may possess or not posses one or several features from the list of features: a1, a2,..., an.
 denotes the absence of the feature
denotes the absence of the feature 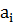 .
.
N(a) denotes the number of objects that posses the feature a (a may be any feature 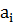 or
or  ).
).
N(a, b, c,..., k) denotes the number of objects, that posses different features a, b, c,..., k (a, b, c,..., k may be 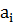 or
or  ).
).
In such a case it is evident:
N( ) = N−N(
) = N−N(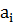 ); (1)
); (1)
N( ) = N− N(
) = N− N( )−N(
)−N( )+N(
)+N( ); (2)
); (2)
The equation (2) is correct because when we subtract N( ) and N(
) and N( ) from the total number of objects, the number N(
) from the total number of objects, the number N( ) is subtracted two times. That is why it must be restored.
) is subtracted two times. That is why it must be restored.
It prompts the name of the method "inclusion and exclusion". the process consists of alternating inclusion of "everything" and exclusion "what is extra".
For a general number of features in the formula of inclusion and exclusion is the following:
N( ) = N −
) = N −  +
+  −
−  +...
+... 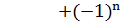 N(
N( ); (3)
); (3)
Formula (3) can be proven by induction by n. When n = 1, n = 2, formulas (1) and (2) where proven using the example.
Let us assume that formula (3) is correct for n−1 features:  . So the following is correct:
. So the following is correct:
N( ) = N −
) = N −  +
+  −
−  +... +
+... +  N(
N( ); (4)
); (4)
Let us apply the formula (4) to the set of objects under consideration that posses the feature an. Remember, we assumed that formula (4) is true for any set of objects and features. In particular, it is correct for the set of N(an) objects. Now we get:
N( ) = N(an) −
) = N(an) −  + +
+ +  −...+
−...+  N(
N( ); (5)
); (5)
By subtracting the formula (5) from the formula (4), we get in the right part, exactly the right part of the equation (3).
In the left part of (4) − (5) we get N( − N(
− N( ) = N(
) = N(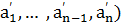 . So we got the equation (3) for any number of features.
. So we got the equation (3) for any number of features.
H/a. there is a certain number of balls. Each ball is painted by one, two or three colors: red, blue and yellow.
Note: 28 balls were colored by red, 23−by blue, 23−by yellow, 12−by red and blue, 8−by blue and yellow, 8−by red and yellow, 5−by all 3 colors.
Question: how many balls were painted?
(Hint: each ball was painted =˃ N(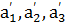 ) = 0).
) = 0).
Date: 2015-12-11; view: 419; Нарушение авторских прав