
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Subtopic: Combinations without repetitions
|
|
Let M be a n – set, M = {a1, a2, …., an}.
k – combinations are different if they differ at least by one element.
Ex: Different 2 – combinations of M = {a,b,c} are as follows: {a,b}, {a,c}, {b,c}. The number of k-combinations that can be generated out of n – district elements is denoted by
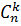 or
or 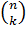 ;
;
Let {b1, b2, …., bk} be some k – combinations of n district elements. Rearranging it in all possible ways we will obtain out of if k! different k–permutations. All permutations obtained in this way are different and each k – permutation can be obtained from some k–combination in this way.
That is why:
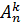 =
= 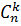 * k!
* k!
From here we receive:
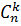 =
= 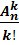 =
= 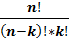 ; (4)
; (4)
It follows immediately from the equality (4):
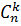 =
=  ; (5)
; (5)
This equality is called the property of symmetry.
Numbers 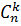 where k
where k  0 or k
0 or k 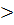 n (as well as 0!) have no combinatorial sense. But it has been to consider that
n (as well as 0!) have no combinatorial sense. But it has been to consider that 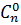 = 1 and
= 1 and 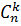 = 0 when k < 0 or k > n.
= 0 when k < 0 or k > n.
For k – combinations such recursion relation holds true:
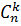 =
= 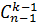 +
+ 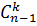 (5)
(5)
Example: It is necessary to select 6 people out of 25 students to go to some meeting. In how many ways the choice can be made?
In this case we are not interested in the sequence of names in the list of “ a delegation”, that is why we consider 3 – combinations.
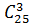 =
= 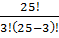 =
= 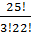 =
= 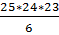 = 2300 ways.
= 2300 ways.
H/t There 16 football teams in the first league and 20 teams in the second league. By the result of a championship two last teams have to leave the first league and two teams from the second league that take the 1 and the 2 places in the 2nd league enter the 1st league. How many variations are there for the exchange of teams between the 1 and 2 leagues at the end of a championship.
H/t There are two parallel lines. One line contains m marked points, another line has n marked points. Each of the m marked points on one line is connected by a straight line with each of n marked points on another parallel line. Among these connecting lines no three line cross in one point. What is the number of cross points of these connecting lines?
H/t In an academic group there are 12 girls and 13 young men. How many dancing pairs can they make during a dancing party?
Topic: Permutations and combinations with unrestricted repetitions.
Subtopic: Basic concepts.
In the previous topics we considered permutations and combinations without repetitions. We assumed that all n elements of the set under consideration are distinct. But in real life we often have to deal with sets where some elements are indistinct, at least within the given problem.
Repetitions of indistinct elements within the initial n – set reduces the number of different permutations and combinations.
For example: if we rearrange the letters in the word “name”, we receive 24 different permutations:”name”, “naem”, “mane” etc. But if we rearrange the letters in the word “mama” in all possible ways then we obtain only 6 different permutations: “mama”, “maam”, “mmaa”, “amam”, “amma”, “aamm”.
We speak about permutations and combinations with repetitions if the initial set M can be presented follows:
M = M1 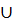 M2
M2 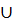 …..
….. 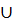 Mn, where Mi
Mn, where Mi  Mj=
Mj= 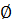 ,
,
Elements within any subset Mi are assumed to be identical and are denoted by mi or just by the number i.
Date: 2015-12-11; view: 464; Нарушение авторских прав