Виды особенностей

В свою очередь, изолированные особенности можно разделить на три вида:

· Устранимая особая точка — точка, в которой функция не определена, но предел функции в которой конечен, соответственно, в этой точке функцию можно доопределить значением этого предела и продолжить её до функции, в этой точке аналитической.

· Полюс — точка, в которой предел функции бесконечен. При рассмотрении функции как отображения не в комплексную плоскость, а в сферу Римана, полюс не следует считать какой-либо особой точкой; см. мероморфная функция.

· Существенно особая точка — точка, в которой предел функции не существует.

10. Точка z ₀ называется с ущественно особой точкой функции f(z), если ряд Лорана функции f(z) в окрестности ее изолированной особой точки z ₀ содержит бесконечно много членов с отрицательными степенями разности (z-z ₀). (Бесконечное число коэффициентов c_-n 0). Поведение аналитической функции в окрестности существенно особой точки описывается следующей теоремой.
Теорема Сохоцкого-Вейерштрасса Для " комплексного числа B и "e >0, в "h - окрестности существенно особой точки z ₀ 0<|z-z₀|< h $ z₁: |f(z₁)-B|< e.
Доказательство. (От противного) Пусть $ такие e ₀ и h ₀: для " z 0<|z-z₀|< h ₀; |f(z)-B|> e ₀. Рассмотрим g(z)=1/[f(z)-B]=> |g(z)|=1/|f(z)-B|<1/ e ₀=M. => z₀ - устранимая особая точка g(z) (по Теореме 16.1); => g(z)=(z-z₀)^m j (z), m 0, j (z₀) 0 => f(z)=B+ ; y (z₀) 0 => z₀- полюс f(z) m 0, или правильная точка при m=0. Получили противоречие. n
Пример. f(z)=e^1/z точка z=0 - существенно особая.

Классификация изолированных особых точек на языке пределов.

Пусть z₀ - изолированная особая точка f(z) C (0<|z-z₀|< r (z₀)).
a) Если при z из окрестности 0<|z-z₀|< r (z₀) и при z z₀ f(z) c₀ |c₀|< , то z ₀ - устранимая особая точка f(z).
b) Если при z из окрестности 0<|z-z₀|< r (z₀) и при z z₀ f(z) , то z ₀ - полюс f(z).
c) Если при z из окрестности 0<|z-z₀|< r (z₀) и при z z₀ f(z) не имеет конечного или бесконечного предела, то z ₀ - существенно особая точка f(z).

Определение. z является изолированной особой точкой однозначной аналитической функции, если $ R>0: для " z: |z|>R f(z) не имеет особых точек, находящихся на конечном расстоянии от точки z=0.
Ряд Лорана в окрестности z : f(z)= c_nzⁿ, R<|z|< .
a) z называется устранимой особой точкой f(z), если все c_n =0 при n>0 f(z)= c_nzⁿ, или $ конечный предел f(z) при z .
b) z называется полюсом f(z) если ряд Лорана функции f(z) в окрестности z содержит конечное число членов с положительными степенями f(z)= c_nzⁿ, (m>0) или f(z) при z .
c) Точка z называется существенно особой точкой функции f(z), если ряд Лорана функции f(z) в окрестности z содержит бесконечно много членов с положительными степенями z: f(z)= c_nzⁿ, или при z у f(z) н ет конечного или бесконечного предела.

11- Пусть — комплекснозначная функция в области , голоморфная в некоторой проколотой окрестности точки .

Вычетом функции в точке называется число

.

В силу голоморфности функции в малой проколотой окрестности точки по теореме Коши величина интеграла не зависит от 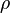при достаточно малых значениях этого параметра, так же как и от формы пути интегрирования. Важно только то, что путь является замкнутой кривой в области аналитичности функции, один раз охватывающей рассматриваемую точку и никаких других точек не принадлежащих области голоморфности .

В некоторой окрестности точки функция представляется сходящимся рядом Лорана по степеням . Нетрудно показать, что вычет совпадает с коэффициентом ряда при . Часто это представление принимают за определение вычета функции.

Вычет в «бесконечности»[править | править исходный текст]

Для возможности более полного изучения свойств функции вводится понятие вычета в бесконечности, при этом она рассматривается как функция на сфере Римана. Пусть бесконечно удалённая точка является изолированной особой точкой , тогда вычетом в бесконечности называется комплексное число, равное

.

Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.

Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удалённой точки:

.

Вычет дифференциальной формы[править | править исходный текст]

С точки зрения анализа на многообразиях вводить специальное определение для некоторой выделенной точки сферы Римана (в данном случае, бесконечно удалённой) неестественно. Более того, такой подход затруднительно обобщить на более высокие размерности. Поэтому понятие вычета вводится не для функций, а для дифференциальных -форм на сфере Римана:

.

На первый взгляд разницы в определениях никакой, однако теперь — произвольная точка , и смена знака при вычислении вычета в бесконечности достигается за счёт замены переменных в интеграле.

Логарифмические вычеты[править | править исходный текст]

Интеграл называется логарифмическим вычетом функции относительно контура .

Понятие логарифмического вычета используется для доказательства теоремы Руше и основной теоремы алгебры

Способы вычисления вычетов[править | править исходный текст]

Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения:

· В устранимой особой точке , так же как и в точке регулярности, вычет функции равен нулю. В то же время для бесконечно удалённой точки это утверждение не верно. Например, функция имеет в бесконечности нуль первого порядка, однако, . Причина этого в том, что форма имеет особенность как в нуле, так и в бесконечности.

· В полюсе кратности вычет может быть вычислен по формуле:

,

частный случай

.

· Если функция имеет простой полюс в точке , где и голоморфные в окрестности функции, , , то можно использовать более простую формулу:

.

· Очень часто, особенно в случае существенно особых точек, удобно вычислять вычет пользуясь разложением функции в ряд Лорана. Например, , так как коэффициент при равен 1.

Вычисления определённых интегралов от тригонометрических функций [править | править исходный текст]

Пусть функция — рациональная функция переменных и . Для вычисления интегралов вида удобно использоватьформулы Эйлера. Положив, что , и произведя соответствующие преобразования, получим:

.

Вычисление несобственных интегралов [править | править исходный текст]

Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:

1. Пусть функция голоморфна в верхней полуплоскости и на вещественной оси за исключением конечного числа полюсов, не лежащих на вещественной оси и . Тогда

.

2. Пусть функция голоморфна в верхней полуплоскости и на вещественной оси за исключением конечного числа полюсов, не лежащих на вещественной оси, и . Тогда

При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).

Date: 2015-12-11; view: 502; Нарушение авторских прав