Доказательство

Рассмотрим окружность S_ρ достаточно малого радиуса ρ с центром в точке z₀. В области, ограниченной контурами Γ и S_ρ подынтегральная функция не имеет особенностей и по интегральной теореме Коши интеграл от неё по границе этой области равен нулю. Это означает, что независимо от ρ имеем равенство:

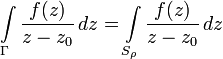
Для расчёта интегралов по 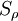применим параметризацию .
Сначала докажем формулу Коши отдельно для случая :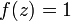

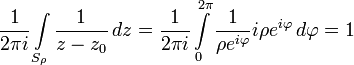
Воспользуемся ею для доказательства общего случая:

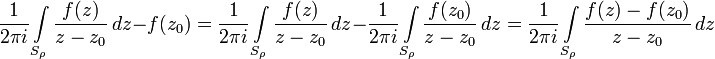
Так как функция комплексно дифференцируема в точке 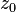, то:

Интеграл от равен нулю:

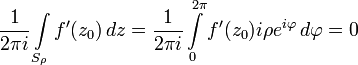
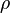Интеграл от члена может быть сделан сколь угодно малым при . Но поскольку он от вообще не зависит, значит он равен нулю. В итоге получаем, что

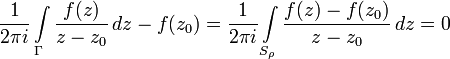
8. Особенность (особая точка) голоморфной функции f — точка комплексной плоскости, в которой эта функция не определена, её предел бесконечен либо предела не существует вовсе.

Для многозначных аналитических функций к особенностям причисляют также точки ветвлений.

Возможны две классификации особых точек. Во-первых, допустима классификация по теоретико-множественным свойствам их множества:

· Изолированная особая точка — точка, для которой существует некоторая проколотая окрестность, в которой эта функция аналитична.

· Неизолированная особая точка — особая точка, не являющаяся изолированной. В этом случае можно говорить о так называемом особом множестве.

Date: 2015-12-11; view: 296; Нарушение авторских прав