Формула Муавра

·

· где — модуль, а 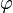— аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формула справедлива при любом целом n, не обязательно положительном.

· Аналогичная формула применима также и при вычислении корней -ой степени из ненулевого комплексного числа:

·

·

·

2. Функция одной переменной –это правило, по которому каждому значению независимой переменной (из области определения) соответствует одно и только одно значение функции . Естественно, x и y– действительные числа.

Однозначная функция комплексной переменной – это правило, по которому каждому комплексному значению независимой переменной (из области определения) соответствует одно и только одно комплексное значение функции .

Понятие обратной функции для функции комплексного переменного вводится, как и в действительной области.

Пусть задана функция 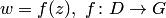. Тогда по определению любому числу из области 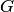соответствует одно или несколько значений из области 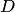таких, что , т.е. для любого уравнение имеет решения и области 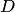. В таком случае говорят, что уравнение определяет функцию , обратную функции .

Существование функции, согласно определению, предполагает ее однотипность, т.е. для случая обратной функции — это единственность решения уравнения при всяком фиксированном из 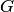. Очевидно, в общем случае уравнение определяет неоднозначную функцию.

Достаточным условием однозначности обратной функции является однолистность функции .

3. Производная для комплексной функции одного аргумента определяется так же, как и для вещественной:

(здесь — комплексное число). Если этот предел существует, функция называется дифференцируемой или голоморфной. При этом

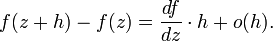
Следует учитывать одну важную особенность: поскольку комплексная функция задана на плоскости, существование приведённого предела означает, что он одинаков при стремлении к с любого направления. Этот факт накладывает существенные ограничения на вид функций-компонент и определяет их жёсткую взаимосвязь (условия Коши — Римана):

Аналити́ческая функция (действительного переменного) — функция, которая совпадает со своим рядом Тейлора в окрестности любой точки области определения.

Однозначная функция называется аналитической в точке 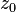, если сужение функции на некоторую окрестность 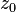является аналитической функцией. Если функция аналитична в точке 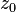, то она аналитическая в каждой точке некоторой окрестности точки .

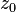Аналитическая функция (комплексного переменного) — функция комплексного переменного (где и — вещественнозначные функции комплексного переменного, являющиеся, соответственно, вещественной и мнимой частью рассматриваемой функции), для которой в каждой точке некоторой односвязной области 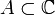, называемой областью аналитичности, выполняется одно из трёх равносильных условий:

1. Для вещественной и мнимой части этой функции в каждой точке выполняются условия Коши — Римана (аналитичность в смысле Коши — Римана);

2. Ряд Тейлора функции в каждой точке сходится и его сумма равна (аналитичность в смысле Вейерштрасса);

3. Интеграл для любой замкнутой кривой 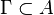(аналитичность в смысле Коши)

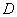5. Пусть - непрерывная функция комплексного , определенная в области и - гладкая кривая, лежащая в 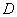, с началом в точке 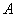и концом в точке (рис. 137), заданная уравнением

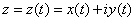
или, что все равно, двумя уравнениями

. (1)

Рис. 137

Как всегда, направление на соответствует изменению параметра от до .

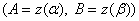Интеграл от функции 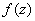вдоль кривой определяется следующим образом:

.

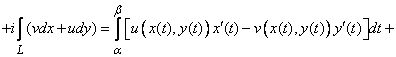
Если учесть, что и , то равенство (2) можно коротко записать так:

. (3)

Интеграл (2) существует для любой непрерывной функции 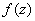(в этом случае функции и 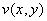также непрерывны) и любой гладкой кривой (т. е. когда , ) непрерывны и ).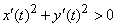

Если кривая кусочно-гладкая и состоит из гладких ориентированных кусков , то по определению считаем

. (4)

На основании свойств криволинейного интеграла легко получаем

1)

,

где та же кривая, что и , но ориентированная противоположно (см. нашу книгу «Высшая математика. Дифференциальное и интегральное исчисление», § 7.4).

2)

,

где 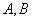- постоянные числа.

3)

Если при , то

,

где 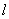- длина .

В самом деле, на основании свойства обыкновенного интеграла имеем

.

6. Пусть — область на комплексной плоскости с кусочно-гладкой границей , функция — голоморфна в и 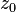— точка внутри области . Тогда справедлива следующая формула Коши:

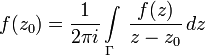
Date: 2015-12-11; view: 357; Нарушение авторских прав