
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации. I. Свойства логарифмов
|
|
I. Свойства логарифмов.
1.Основное логарифмическое тождество: 
2. 
3. 
4. 
5. 
6. 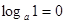
7. 
8.  - формула перехода к другому основанию
- формула перехода к другому основанию
9. 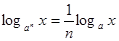
II. Логарифмические уравнения.
Определение. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.  ,
,  ,
,  . – простейшее логарифмическое уравнение.
. – простейшее логарифмическое уравнение.
Уравнение вида  равносильно системе:
равносильно системе: 
Методы решения.
1. Полученные корни подставляют в исходное уравнение для исключения посторонних корней.
2. При решении уравнений полезен метод введения новой переменной.
3. При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования.
Примеры.
1. 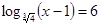
 , ,  По определению логарифма:
По определению логарифма:


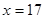 Ответ: 17.
Ответ: 17.
| 2. 



 Пусть
Пусть  , тогда , тогда


 или или 
 или или 
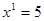 или или 
 или или  Ответ: 5;
Ответ: 5;  . .
|
III. Логарифмические неравенства.
Определение. Неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим неравенством.

при  , данное неравенство равносильно системе неравенств
, данное неравенство равносильно системе неравенств 
при  , данное неравенство равносильно системе неравенств
, данное неравенство равносильно системе неравенств 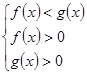
Примеры.
1. 
 , т.к.
, т.к.  , то переходим к системе неравенств:
, то переходим к системе неравенств:




 , т.е.
, т.е. 
Варианты заданий практической работы
| 1 вариант | 2 вариант |
А1. Укажите промежуток, которому принадлежит корень уравнения:
 1)
1)  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4) 
| А1. Укажите промежуток, которому принадлежит корень уравнения:
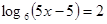 1)
1)  ; 2) ; 2)  ; 3) ; 3) 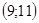 ; 4) ; 4) 
|
А2. Найдите произведение корней уравнения:  1)
1)  2) 2)  3) 3) 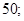 4) 4) 
| А2. Найдите произведение корней уравнения:  1)
1) 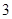 ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
|
А3. Решите неравенство:
 1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
| А3. Решить неравенство:
  1)
1)  ; 2) ; 2)  ; 3) ; 3) 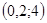 ; 4) ; 4) 
|
А4. Решите неравенство:  1)
1)  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4) 
| А4. Решить неравенство:  1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
|
В1. Решите уравнение: 
| В1. Решите уравнение: 
|
В2. Решите уравнение:
 . В ответе укажите наименьший из корней данного уравнения. . В ответе укажите наименьший из корней данного уравнения.
| В2. Решите уравнение:
 . В ответе укажите наибольший из корней данного уравнения. . В ответе укажите наибольший из корней данного уравнения.
|
В3. Найдите наибольшее целое значение  , удовлетворяющее неравенству: , удовлетворяющее неравенству: 
| В3. Найдите наименьшее целое значение  , удовлетворяющее неравенству: , удовлетворяющее неравенству: 
|
С1. Решите систему уравнений:

| С1. Решите систему уравнений:
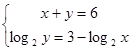
|
| 3 вариант | 4 вариант |
А1. Укажите промежуток, которому принадлежит корень уравнения:
 1)
1)  ; 2) ; 2)  ; 3) ; 3) 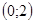 ; 4) ; 4) 
| А1. Укажите промежуток, которому принадлежит корень уравнения:
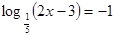 1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
|
А2. Найдите произведение корней уравнения:  1)
1) 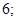 2) 2)  3) 3)  4) 4) 
| А2. Найдите произведение корней уравнения:  1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
|
А3. Решите неравенство:
 1)
1)  ; 2) ; 2) 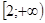 ; 3) ; 3)  ; 4) ; 4)  нет реш. нет реш.
| А3. Решите неравенство:
 1)
1)  ; 2) ; 2)  ; 3) ; 3)  ;
4) ;
4) 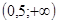
|
А4. Решите неравенство:  1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 
| А4. Решите неравенство:  1)
1)  ; 2) ; 2)  ; 3) ; 3)  ; 4) ; 4) 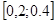
|
В1. Решите уравнение: 
| В1. Решите уравнение: 
|
В2. Решите уравнение:
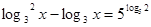 . В ответе укажите наименьший корень данного уравнения . В ответе укажите наименьший корень данного уравнения
| В2. Решите уравнение:
 . В ответе укажите наибольший корень данного уравнения. . В ответе укажите наибольший корень данного уравнения.
|
В3. Найдите наибольшее целое значение  ,удовлетворяющее неравенству: ,удовлетворяющее неравенству: 
| В3. Найдите наименьшее целое значение, удовлетворяющее неравенству: 
|
С1. Решите систему уравнений:

| С1. Решите систему уравнений:
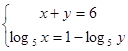
|
Date: 2015-12-10; view: 1080; Нарушение авторских прав