Лінійні однорідні д. р. другого порядку із сталими коефіцієнтами. Теорема про структуру загального розв’язку

Рівняння вигляду:

,

де p і q – відомі сталі, f(x) – відома функція називається лінійним д. р. ІІ-го порядку із сталими коефіцієнтами. Якщо , то д. р.

називається лінійним однорідним д. р. (скорочено ЛОДР) із сталими коефіцієнтами.

Якщо ж 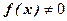, то перше з д. р. називається неоднорідним (ЛНДР)

Теорема: Якщо функції і є розв’язками д. р.

,

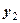то функція , де С₁ і С₂ довільні сталі, теж є розв’язком цього д. р., тобто лінійна комбінація двох розв’язків і теж є розв’язком ЛОДР.

Доведення. Згідно умови теореми маємо

Після почленного домноження на довільні сталі С₁ і С₂ кожної з рівностей та додавання їх, отримаємо:

.

Згідно властивості лінійної операції диференціювання можемо записати

.

Тому, далі, маємо

,

а це означає, що функція теж є розв’язком ЛОДР.

Означення. Дві функції і 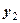називаються лінійно незалежними, якщо їх відношення , тобто .

Якщо ж , тобто , то функції і називаються лінійно залежними.

Приклади.1. Функції 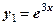і - лінійно незалежні, бо .

2. Функції і - лінійно незалежні, бо .

3. Функції і - лінійно залежні, бо , тобто .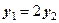

Постановка Задачі Коші, як і для д. р. І-го порядку, полягає в тому, щоб знайти розв’язок ЛОДР

при початкових умовах , .

Важливою для розв’язання задачі Коші є така теорема (подаємо без доведення).

Теорема. (про структуру загального розв’язку ЛОДР). Якщо і - лінійно незалежні розв’язки ЛОДР

,

де p і q – сталі, то загальний розв’язок цього рівняння має вигляд

,

де С₁ і С₂ довільні сталі.

Через позначено загальний розв’язок однорідного д. р.

Date: 2015-12-10; view: 608; Нарушение авторских прав