
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задания для самостоятельного решения. 1. Исследовать совместность следующих систем
|
|
1. Исследовать совместность следующих систем.
а)  б)
б) 
в)  г)
г) 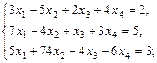
д) 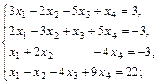 е)
е) 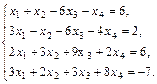
2. Решить системы уравнений матричным методом:
а)  б)
б) 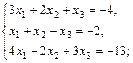
в)  г)
г) 
д) 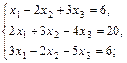 е)
е) 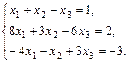
3. Решить системы уравнений по формулам Крамера:
а) 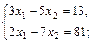 б)
б) 
в) 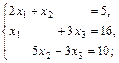 г)
г) 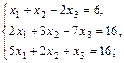
д)  е)
е) 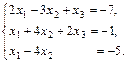
4. Решить системы уравнений методом Гаусса:
а) 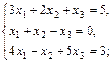 б)
б) 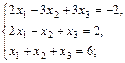
в) 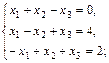 г)
г) 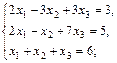
д) 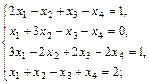 е)
е) 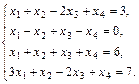
5. Найти фундаментальную систему решений и общее решение следующих систем:
а) 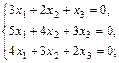 б)
б) 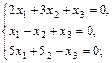
в)  г)
г) 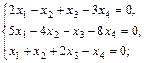
д)  е)
е) 
Ответы. 1. а) система несовместна; б) система совместна;
в) система совместна; г) система несовместна; д) система совместна; е) система совместна. 2. а)  ; б) (-3;2;1); в) (3;0;1); г) (3;-2;-5); д) (8;4;2); е) (-8;-4;-13). 3. а) (16;7); б) (2;-1;1); в) (1;3;5); г) (3;1;-1);
; б) (-3;2;1); в) (3;0;1); г) (3;-2;-5); д) (8;4;2); е) (-8;-4;-13). 3. а) (16;7); б) (2;-1;1); в) (1;3;5); г) (3;1;-1);
д) (-3;2;1); е) (-1;1;-2). 4. а) (-1;3;2); б) (2;3;1); в) (2;1;3); г) (3;2;1); д) ( ); е) (
); е) ( ). 5. а) (
). 5. а) (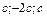 ); б) (0;0;0); в) (0;0;0); г)
); б) (0;0;0); в) (0;0;0); г) 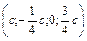 ; д)
; д)  ;
;
е)  .
.
Индивидуальное домашнее задание по теме «Элементы линейной алгебры»
Задание. Доказать совместность данной системы линейных уравнений и решить ее тремя способами: 1) методом Гаусса; 2) матричным методом; 3) по формулам Крамера.
1. 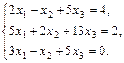 2.
2. 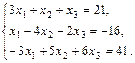
3. 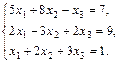 4.
4. 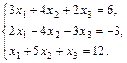
5. 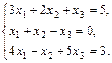 6.
6. 
7.  8.
8. 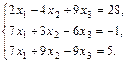
9. 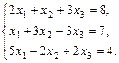 10.
10. 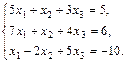
11. 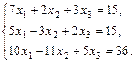 12.
12. 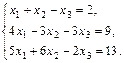
13. 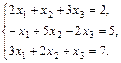 14.
14. 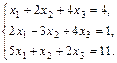
15.  16.
16. 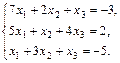
17. 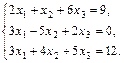 18.
18. 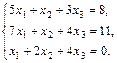
19. 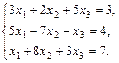 20.
20. 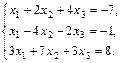
21. 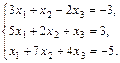 22.
22. 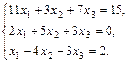
23. 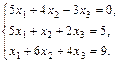 24.
24. 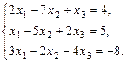
25. 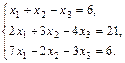
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Векторы. Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Например, площадь, длина, работа, масса. Величины, которые определяются не только своим числовым значением, но и направлением, называются векторными. Например, сила, ускорение.
Определение. Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий определенную длину и определенное направление. Если точка А – начало вектора, а точка В – его конец, то вектор обозначается символом  или
или  .
.
Определение. Вектор  (у него начало в точке В, а конец в точке А) называется противоположным вектору
(у него начало в точке В, а конец в точке А) называется противоположным вектору  . Вектор, противоположный вектору
. Вектор, противоположный вектору  обозначается
обозначается  .
.
Определение. Расстояние между началом и концом вектора называется его длиной или модулем и обозначается 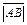 .
.
Определение. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается  . Нулевой вектор не имеет определенного направления.
. Нулевой вектор не имеет определенного направления.
Определение. Вектор, длина которого равна единице, называется единичным вектором и обозначается 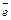 . Единичный вектор, направление которого совпадает с направлением вектора
. Единичный вектор, направление которого совпадает с направлением вектора  , называется ортом (орт) вектора
, называется ортом (орт) вектора  и обозначается
и обозначается 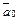 .
.
Определение. Векторы  и
и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, обозначается коллинеарность
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, обозначается коллинеарность  . Коллинеарные векторы могут быть сонаправлены (
. Коллинеарные векторы могут быть сонаправлены (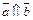 ) и противоположно направлены (
) и противоположно направлены (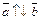 ).
).
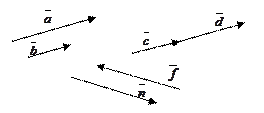
 кроме того
кроме того 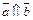 ,
, 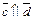 ,
, 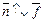 .
.
Определение. Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

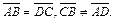
Определение. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
Date: 2015-12-10; view: 298; Нарушение авторских прав