Метод Гаусса

Рассмотрим задачу решения системы линейных алгебраических уравнений

.

Здесь - заданная квадратная матрица размера

,

и соответственно заданный вектор свободных членов и вектор неизвестных

, .

В явном виде система может быть записана также как

,

или

.

Метод Гаусса основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Метод Гаусса включает в себя два этапа: прямой и обратный ход.

1) Прямой ход. Предположим, что коэффициент , называемый ведущим элементом первой строки, не равен нулю. Разделим первое уравнение на этот коэффициент. В результате оно примет вид

,

где , . Затем с помощью полученного уравнения во всех остальных уравнениях системы исключим слагаемые, содержащие . Для этого умножим это уравнение на и вычтем из второго уравнения, умножим на и вычтем из третьего уравнения и т.д. В результате уравнения системы, начиная со второго, примут вид

,

где , . Подобным образом преобразуем эти уравнения, т.е. разделим второе уравнение на и с помощью полученного уравнения во всех остальных уравнениях, начиная с третьего, исключим слагаемые, содержащие . Этот процесс будем продолжать до тех пор, пока в левой части последнего, -го, уравнения не останется лишь один член с неизвестным . В результате исходная система будет приведена к эквивалентной форме с верхней треугольной матрицей:

.

2) Обратный ход. Он состоит в последовательном вычислении искомых неизвестных. Сначала из последнего уравнения определяем . Используя это значение, из предыдущего уравнения находим . И т.д. Последним найдем из первого уравнения. Таким образом, для отыскания неизвестных имеем рекуррентную формулу

.

Вычисление определителей. В прямом ходе процедуры Гаусса матрица системы приводится к треугольному виду с помощью операций двух типов:

1) Деление всех элементов строки на ведущий элемент этой строки. При этом, как известно из линейной алгебры, определитель матрицы также делится на этот ведущий элемент.

2) Добавление к элементам строки элементов другой строки, умноженных на константу. Определитель матрицы при такой операции не изменяется.

Таким образом, если обозначить через полученную в результате этих преобразований треугольную матрицу, то

.

С другой стороны, определитель треугольной матрицы, на главной диагонали которой находятся только единицы, равен единице. Следовательно, определитель исходной матрицы равен произведению ведущих элементов строк:

.

Таким образом, при решении системы линейных алгебраических уравнений методом Гаусса “попутно” можно вычислить определитель матрицы этой системы. Если же требуется только найти определитель заданной матрицы, то вычисления проводятся по схеме, соответствующей прямому ходу метода Гаусса. Отличие лишь в том, что отсутствуют действия над столбцом свободных членов.

Рассмотренный выше простейший вариант метода Гаусса называется схемой единственного деления. Он обладает рядом недостатков. Если ведущий элемент какой-либо строки, например , окажется равным нулю, то эта схема формально непригодна. Возможен также более неприятный случай, когда ведущий элемент не нулевой, но очень мал по модулю по сравнению с другими элементами строки. Тогда при делении на это малое число получаются очень большие числа. Это приводит к значительному росту погрешности округлений. Как следствие, точность результата становится очень плохой, даже катастрофически плохой.

Изложим теперь схему метода Гаусса, свободную от этих недостатков. Она называется схемой с выбором главного элемента и в алгоритмическом плане незначительно отличается от предыдущей.

Пусть, как и прежде, дана система линейных алгебраических уравнений

.

Сначала добиваемся выполнения условий

.

Для этого отыскиваем максимальный по модулю элемент матрицы и при необходимости переставляем два уравнения и два столбца исходной системы. Затем производим соответствующую перенумерацию коэффициентов и неизвестных. Найденный максимальный по модулю коэффициент называется первым главным элементом. После этого выполняем как обычно первый шаг процедуры Гаусса, т.е. во всех уравнениях системы, начиная со второго, исключаем слагаемые, содержащие . В полученной “урезанной” системе находим второй главный элемент, т.е. добиваемся

,

и повторяем процедуру.

В этом случае также можно вычислить определитель исходной матрицы . Из линейной алгебры известно, что при перестановке двух строк или столбцов матрицы определитель меняет знак. Поэтому в полученную формулу для определителя необходимо добавить множитель , где - полное число перестановок строк и столбцов на всех этапах приведения матрицы к треугольному виду. В результате формула для определителя приобретает вид

.

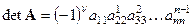Может случиться, что система вырождена, т.е. ее определитель . Это приведет к тому, что на некотором шаге главный элемент окажется равным нулю (т.е. равны нулю и все элементы ниже него). Поэтому на каждом шаге нужно контролировать обращение в нуль главного элемента. Решение вырожденных систем рассматривалось в курсе линейной алгебры и здесь мы рассматривать этот вопрос не будем.

Date: 2015-12-10; view: 540; Нарушение авторских прав