
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 3. Механическая система (рис
|
|
Механическая система (рис. 3.4) состоит из груза 1 массой  ; блока 2 (сплошного однородного диска) массой
; блока 2 (сплошного однородного диска) массой  и радиусом
и радиусом  ; тонкого однородного стержня 3 массой
; тонкого однородного стержня 3 массой  и длиной
и длиной 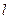 ; сплошного однородного диска 4 массой
; сплошного однородного диска 4 массой 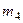 и радиусом
и радиусом  . Система начинает двигаться из положения покоя
. Система начинает двигаться из положения покоя  (при статической деформации пружины с коэффициентом жесткости
(при статической деформации пружины с коэффициентом жесткости  ) с начальным отклонением
) с начальным отклонением 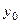 груза 1 по вертикали от положения покоя и проекцией
груза 1 по вертикали от положения покоя и проекцией 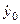 его начальной скорости
его начальной скорости  .
.
 Дано:
Дано:  кг,
кг,  кг,
кг,  кг,
кг,  кг,
кг,  м,
м,  Н/см,
Н/см,  см,
см,  см/с.
см/с.
Определить: циклическую частоту  и период
и период  малых свободных колебаний системы, получить уравнение движения груза 1
малых свободных колебаний системы, получить уравнение движения груза 1 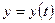 и найти амплитуду
и найти амплитуду  его колебаний.
его колебаний.
Решение:
1) Рассмотрим произвольное положение системы, когда она выведена из состояния равновесия и совершает малые колебания (рис. 3.4). Механическая система имеет одну степень свободы. В качестве обобщенной координаты выберем координату 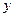 перемещения груза 1. Поскольку все действующие активные силы (силы тяжести и сила упругости) потенциальные, воспользуемся уравнением Лагранжа II рода для консервативной системы:
перемещения груза 1. Поскольку все действующие активные силы (силы тяжести и сила упругости) потенциальные, воспользуемся уравнением Лагранжа II рода для консервативной системы:
 , (3.1)
, (3.1)
где  и
и  – кинетическая и потенциальная энергии системы, соответственно.
– кинетическая и потенциальная энергии системы, соответственно.
При исследовании малых колебаний в уравнении сохраняют малые величины 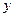 ,
,  в первой степени, отбрасывая малые более высокого порядка. Для этого надо найти выражения для
в первой степени, отбрасывая малые более высокого порядка. Для этого надо найти выражения для  и
и  с точностью до
с точностью до  ,
,  , так как в уравнение (3.1) входят первые производные от
, так как в уравнение (3.1) входят первые производные от  и
и  по
по 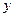 и
и  , а при дифференцировании многочлена его степень понижается на единицу.
, а при дифференцировании многочлена его степень понижается на единицу.
2) Определим кинетическую энергию всей системы, равную сумме кинетических энергий всех тел:
 . (3.2)
. (3.2)
Груз 1 движется поступательно, блок 2 истержень 3 вращаются вокруг неподвижной оси, диск 4 совершает плоскопараллельное движение, поэтому
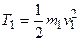 ,
,  ,
,  ,
,
 . (3.3)
. (3.3)
Моменты инерции блока 2 и стержня 3 относительно оси вращения и диска 4 относительно центральной оси имеют вид:
 ,
, 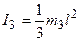 ,
, 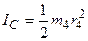 . (3.4)
. (3.4)
Скорости  ,
,  и угловые скорости
и угловые скорости  ,
,  и
и  тел системы выразим через обобщенную скорость
тел системы выразим через обобщенную скорость  :
:
 ,
,  ,
,  . (3.5)
. (3.5)
Скорость  и угловую скорость
и угловую скорость  найдем, учитывая, что рассматриваются малые колебания (значит
найдем, учитывая, что рассматриваются малые колебания (значит  ) и диск 4 катится без скольжения (точка
) и диск 4 катится без скольжения (точка  – мгновенный центр скоростей тела 4):
– мгновенный центр скоростей тела 4):
 . (3.6)
. (3.6)
Учитывая соотношения (3.3) – (3.6) приведем выражение (3.2) к виду:
 . (3.7)
. (3.7)
Так как кинетическая энергия зависит только от  , производные левой части уравнения (1) примут вид:
, производные левой части уравнения (1) примут вид:
 ;
;
 ; (3.8)
; (3.8)
 .
.
3)  Найдем потенциальную энергию
Найдем потенциальную энергию  системы (см. рис. 3.5) как сумму работ сил тяжести тел системы и силы упругости пружины на перемещении из отклоненного положения системы (когда груз 1 имеет координату
системы (см. рис. 3.5) как сумму работ сил тяжести тел системы и силы упругости пружины на перемещении из отклоненного положения системы (когда груз 1 имеет координату 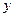 ) в начальное (состояние покоя):
) в начальное (состояние покоя):
 , (3.9)
, (3.9)
 где
где  и
и  – потенциальные энергии, соответствующие силам тяжести тел системы и силе упругости пружины на перемещении.
– потенциальные энергии, соответствующие силам тяжести тел системы и силе упругости пружины на перемещении.
 , (3.10)
, (3.10)
где  – вертикальное смещение центра тяжести стержня.
– вертикальное смещение центра тяжести стержня.
Вычислим его с точностью до величины второго порядка малости относительно обобщенной координаты 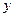 (см. рис. 3.5):
(см. рис. 3.5):
 . (3.11)
. (3.11)
Учитывая малость угла  , разложим
, разложим 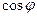 в ряд Тейлора:
в ряд Тейлора:
 (3.12)
(3.12)
Ограничиваясь в разложении (3.12) двумя первыми членами и учитывая, что
 ,
,
получаем из (3.11):
 . (3.13)
. (3.13)
Подставив (3.13) в (3.10) находим:
 . (3.14)
. (3.14)
Потенциальная энергия деформированной пружины 3 равна
 , (3.15)
, (3.15)
где  – статическая деформация пружины 3, соответствующая начальному отклонению
– статическая деформация пружины 3, соответствующая начальному отклонению 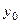 груза 1 по вертикали от положения покоя;
груза 1 по вертикали от положения покоя;  – перемещение точки прикрепления
– перемещение точки прикрепления  пружины 3, соответствующее координате
пружины 3, соответствующее координате 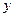 груза 1.
груза 1.
Из рис. 3.4 определяем
 ,
,
откуда
 . (3.16)
. (3.16)
Таким образом, потенциальная энергия пружины 3
 , (3.17)
, (3.17)
а потенциальная энергия механической системы

 (3.18)
(3.18)
Учитывая, что в состоянии покоя, соответствующем статической деформации пружины 3
 ,
,  , (3.19)
, (3.19)
приводим (3.18) к виду:
 (3.20)
(3.20)
 Уравнение 3.19 можно также получить, составив одно из условий равновесия системы сил для положения покоя (см. рис. 3.6):
Уравнение 3.19 можно также получить, составив одно из условий равновесия системы сил для положения покоя (см. рис. 3.6):
 :
:
 или
или
 .
.
Отсюда  .
.
 Выполним операцию дифференцирования потенциальной энергии системы, предусмотренную правой частью уравнения (3.1):
Выполним операцию дифференцирования потенциальной энергии системы, предусмотренную правой частью уравнения (3.1):
 , (3.21)
, (3.21)
Подставим (3.8) и (3.21) в (3.1):
 (3.22)
(3.22)
или, обозначив
 , (3.23)
, (3.23)
приведем (3.22) к виду:
 . (3.24)
. (3.24)
Уравнение (3.24) является уравнением свободных колебаний с частотой  . Подставив в (3.23) численные значения, находим:
. Подставив в (3.23) численные значения, находим:
 с–1. (3.25)
с–1. (3.25)
Период свободных колебаний
 с. (3.26)
с. (3.26)
Интегрируя уравнение (3.24), находим уравнение движения груза 1:
 . (3.27)
. (3.27)
Для определения констант интегрирования 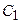 и
и  составим уравнение скорости груза 1:
составим уравнение скорости груза 1:
 (3.28)
(3.28)
и воспользуемся начальными условиями:
при 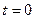
 ,
,  . (3.29)
. (3.29)
Из уравнений (3.27) – (3.29) находим:
 ,
, 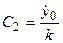 .
.
И окончательно:
 м. (3.30)
м. (3.30)
Уравнение (3.30) можно представить в эквивалентной форме, если использовать другие константы интегрирования  и
и  :
:
 ,
,  .
.
Тогда
 ,
,
 м, (3.31)
м, (3.31)
 рад.
рад.
Таким образом
 м.
м.
Ответ:  с–1,
с–1,  с,
с,  м,
м,  м.
м.
Date: 2015-12-10; view: 687; Нарушение авторских прав