
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расстояние переезда
|
|
Для определения оптимальной величины интервала h используют формулу Стерджеса:
h =  ,
,
где раст. переездаmax, раст. переездаmin - максимальное и минимальное значение времени простой реакции в исследуемом вариационном ряду, с.;
N- общее число наблюдений. N=29.
h =  =
=  =2,3 с.
=2,3 с.
h = 2,3 c.
Vср = - 0,576 сек;
Построение интервального вариационного ряда.
Таблица 8
| Границы интервалов, с. | Середины интервалов Vci, с. | Опытные частоты, mi* | Опытные частости, Pi* | Накопленные частости, F(v) | mi* *Vci, | mi* *V2ci, | (Vci- Vср)3 * Pi* | (Vci, - Vср)4 * Pi* | |
| (-12) – (-9,7) | -10,85 | 0,034 | 0,034 | -10,85 | 117,72 | -36,87 | 378,82 | ||
| (-9,7) – (-7,4) | -8,55 | 0,034 | |||||||
| (-7,4) – (-5,1) | -6,25 | 0,034 | |||||||
| (-5,1) – (-2,8) | -3,95 | 0,068 | 0,068 | -7,9 | 31,205 | -2,612 | 8,812 | ||
| (-2,8) – (-0,5) | -1,65 | 0,484 | 0,136 | -23,1 | 38,115 | -0,599 | 0,644 | ||
| (-0,5) – 1,8 | 0,65 | 0,276 | 0,620 | 5,2 | 3,38 | 0,508 | 0,623 | ||
| 1,8 – 4,1 | 2,95 | 0,138 | 0,862 | 11,8 | 34,81 | 6,049 | 21,331 | ||
| Сумма | - | - | -24,85 | 225,23 | -33,52 | 410,23 | |||

Рисунок 7 - Интервалы расстояния переезда.
Красным цветом обозначен интервал, в который входит значение ВПР студента.
Из графика видно, что данное распределение близок к распределению Вейбулла.
Рассчитаем статистические параметры:
Математическое ожидание:
 =
= 
 раст. переезда =
раст. переезда =  =
=  = -0,857 сек;
= -0,857 сек;
Статическая дисперсия:
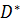 (V) =
(V) =  -
-  ;
;
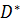 (V)раст. переезда=
(V)раст. переезда=  -
-  =
=  -
-  = 7,03;
= 7,03;
Несмещенная оценка дисперсии:
D(V) =  *
* 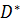 (V)раст. переезда;
(V)раст. переезда;
D(V)раст. переезда =  *7,03 = 7,28;
*7,03 = 7,28;
Стандартное среднеквадратическое отклонение:
 =
=  ;
;
 =
=  = 2,698 сек;
= 2,698 сек;
Коэффициент вариации:
ν=  *100%;
*100%;
νраст. переезда=  * 100% = 314,82%;
* 100% = 314,82%;
Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:
В данном случае коэффициент вариации более 33%, следовательно это говорит о неоднородности информации и необходимости исключения самых больших и самых маленьких значений.
Ассиметрия:
 =
=  ∑
∑  *
*  ;
;
As раст. переезда =  *(-33,52) = -1,707;
*(-33,52) = -1,707;
В данном случае видно, что распределение левостроннее.
Эксцесс:
EK= 
 *Pi – 3;
*Pi – 3;
EKраст. переезда =  * 410,23– 3 = 4,74;
* 410,23– 3 = 4,74;
Данный график распределения имеет более острую вершину, т.к. коэффициент эксцесса больше нуля.
Память
Для определения оптимальной величины интервала h используют формулу Стерджеса:
h =  ,
,
где Памятьmax, Памятьmin - максимальное и минимальное значение времени простой реакции в исследуемом вариационном ряду, %;
N- общее число наблюдений. N=29.
h =  =
=  = 13,657 %.
= 13,657 %.
h = 14 %.
Vср = 82 %;
Построение интервального вариационного ряда.
Таблица 9
| Границы интервалов, %. | Середины интервалов Vci, с. | Опытные частоты, mi* | Опытные частости, Pi* | Накопленные частости, F(v) | mi* *Vci, | mi* *V2ci, | (Vci, - Vср)3 * Pi* | (Vci, - Vср)4 * Pi* |
| 14-28 | 0,07 | 0,07 | -15888 | |||||
| 28-42 | 0,034 | 0,1 | -3530 | |||||
| 42-56 | 0,034 | 0,14 | -1222 | |||||
| 56-70 | 0,1 | 0,24 | -686 | |||||
| 70-84 | 0,07 | 0,31 | -8,75 | 43,75 | ||||
| 84-98 | 0,31 | 0,62 | ||||||
| 98-112 | 0,38 | |||||||
| Сумма | - | - | -16486 |

Рисунок 8 - Интервалы Памяти
Красным цветом обозначен интервал, в который входит значение Памяти студента.
Из графика видно, что данное распределение близко к логарифмическому.
Рассчитаем статистические параметры:
Математическое ожидание:
 =
= 
 память =
память =  =
=  = 84;
= 84;
Статическая дисперсия:
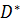 (V) =
(V) =  -
-  ;
;
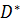 (V)память=
(V)память=  -
-  =
=  -
-  =630;
=630;
Несмещенная оценка дисперсии:
D(V) =  *
* 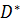 (V)память;
(V)память;
D(V)впр =  *630 =653;
*630 =653;
Стандартное среднеквадратическое отклонение:
 =
=  ;
;
 =
= 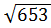 = 25,5;
= 25,5;
Коэффициент вариации:
ν=  *100%;
*100%;
νпамять=  * 100% =30,3%;
* 100% =30,3%;
Коэффициент вариации характеризует относительную меру отклонения измеренных значений от среднеарифметического:
В данном случае коэффициент вариации менее 33%, следовательно это говорит о однородности информации.
Ассиметрия:
 =
=  ∑
∑  *
*  ;
;
Asвпр =  *(-16486) = -0,98;
*(-16486) = -0,98;
В данном случае видно, что распределение левосторонее.
Эксцесс:
EK= 
 *Pi – 3;
*Pi – 3;
EKвпр =  *1296888– 3 =0,04;
*1296888– 3 =0,04;
Данный график распределения имеет более острую вершину.
Вывод:
В результате данной лабораторной работы было изучено влияние психофизиологических качеств (таких как время простой реакции, время сложной реакции, время сложной реакции с помехами, помехоустойчивость, коэффициент концентрации внимания, коэффициент устойчивости внимания, расстояние переезда и память) на эффективность производственной деятельности.
Параметры, которые были рассчитаны в данной работе, у различных людей разные и зависят от множества факторов. Следовательно, целесообразно сравнивать свои результаты не с результатами других студентов, а со средним значением группы.
Данные сведены в таблицу:
| Фамилия | ВПР | ВСР | νвср | ВСРсП | П | Кк | Ку | Раст.переезд., % | Память, % |
| Перфильева | 0,254 | 0,464 | 0,125 | 0,582 | 0,118 | 1,085 | 1,477 | -0,911 | |
| Среднее значение | 0,2377 | 0,507 | - | 0,481 | -0,026 | - 0,576 |
Из этой таблицы видно что:
· Время простой реакции на 0,0163с превышает среднее значение;
· Время сложной реакции на 0,043с меньше среднего значения;
· Время сложной реакции с помехами на 0,101с больше среднего значения;
· Помехоустойчивость на 0,092 больше среднего значения;
· Коэффициент концентрации внимания на 0,085 больше среднего значения;
· Коэффициент устойчивости внимания на 0,447 больше среднего значения;
· Расстояние переезда на 0,335% больше среднего значения;
· Память на 18% больше среднего значения.
Если по каждому параметру проанализировать диапазон в который попадает моё значение можно сделать следующий вывод:
1) в диапазон значений простой реакции (0,235-0,265) входит 6 студентов нашей группы;
2) в диапазон значений сложной реакции (0,455-0,505) входит 8 студентов;
3) в диапазон значений сложной реакции с помехой (0,465-0,54) входит 13 студентов;
4) в диапазон значений помехоустойчивости (0-0,06) входит 5 студентов;
5) в диапазон значений коэффициента концентрации внимания (1,0-1,1) входит 8 студентов;
6) в диапазон значений коэффициента устойчивости внимания (1,0-1,5) входит 20 студентов;
7) в диапазон значений расстояния переезда (-2,8- (-0,5)) входит 14 студентов;
8) в диапазон значений памяти (98-112) входит 11 студентов.
С полученными результатами согласна.
Память 100%, остальные результаты неплохие, кроме расстояния переезда, оно желает лучшего. Следует на это обратить внимание.
Date: 2015-11-13; view: 370; Нарушение авторских прав