Решения уравнений движения

Одной из предпосылок к математическому моделированию колебаний горной машины на примере карьерного экскаватора и выбору математического аппарата является то, что эта машина состоит из ряда крупных соединенных между собой взаимно подвижных и неподвижных узлов. Поворотной платформы, на которой размещены двуногая стойка стрелы, преобразовательные агрегаты, механизмы подъема и напора ковша, механизм поворота, электрические шкафы управления экскаватором. Верхняя секция стрелы и рукоять с ковшом, соединены со стрелой и барабанами механизмов подъема и напора ковша стальными канатами, представляющими собой упругодемпфирующие связи «пружины» растяжения. Механизм хода размещен под поворотной платформой. При работе экскаватора в зависимости от технологических операций рабочего цикла погрузки реверсивные приводы подъема и напора по отдельности или одновременно приводят в движение рукоять с ковшом, который по траектории близкой к логарифмической спирали движется относительно поворотной платформы экскаватора. Платформа экскаватора осуществляет повороты в сторону забоя для черпания или в сторону транспортного средства для разгрузки ковша. Таким образом, мы имеем многомассовую систему с несколькими степенями свободы.

При описании колебательного движения механической системы отдельных узлов экскаватора, соединенных упругодемпфирующими связями, с N степенями свободы следует ввести N колебательных координат S_i, характеризующих смещение частей системы из положения равновесия.

В качестве колебательных координат можно выбрать изменения величин, характеризующих относительное расположение отдельных частей механической системы: изменение длин связей и углов между связями, изменение расстояний между несвязанными частями системы. Такие относительные координаты получили название естественных или внутренних координат.

Выбор естественных координат не является однозначным, и используется для упрощения математической части задачи.

Для математического описания механической системы модели экскаватора воспользуемся основными теоретическими положениями, разработанными применительно к колебаниям систем с конечным числом степеней свободы [59, 101, 102].

Потенциальная энергия U системы является функцией естественных колебательных координат:

(5.1)

Вблизи минимума, т.е. вблизи точки , функцию U удобно разложить в ряд по степеням S_i:

(5.2)

где , если отсчитывать потенциальную энергию от её минимума.

В силу условия равновесия , а кубическими и высшими членами в разложении (5.2) можно пренебречь в случае достаточно малых амплитуд колебаний. Так что, используя матричную форму [59] записи основных уравнений можно представить

, (5.3)

где 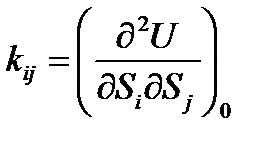, причём . (5.4 Последнее обстоятельство - симметрия коэффициентов k_ij,, значительно сокращает объём вычислений и позволяет выбрать наиболее короткий путь при расчётах.

Кинетическая энергия колебательного движения может быть выражена формулой:

, (5.5)

Здесь точка над координатами означает производную по времени.

Матрица коэффициентов , как и матрица коэффициентов k_ij является симметричной.

Для получения уравнений движения отдельных частей системы, совершающей малые колебания, воспользуемся уравнениями Гамильтона:

. (5.6)

Здесь q_i - независимые обобщённые координаты, например, естественные колебательные координаты S_i, а p_i - обобщённые импульсы, которые определяются по формулам:

, (5.7)

H - функция Гамильтона системы, равная сумме её потенциальной и кинетической энергий:

, (5.8)

причём кинетическая энергия, выраженная через обобщённые импульсы, равна:

, , (5.9)

где A_ij - элементы матрицы, обратной матрице m_ij.

В дальнейшем матрицу А будем называть матрицей кинематических коэффициентов, а матрицу k - матрицей силовых коэффициентов.

Подставляя (5.3) и (5.9) в (5.8) и затем в (5.6), получим:

, (5.10)

, (5.11)

откуда, дифференцируя (5.11) по времени и используя (5.10), получим систему дифференциальных уравнений:

, , (5.12)

описывающих малые колебания рассматриваемой механической системы.

Одним из возможных частных решений системы дифференциальных уравнений (5.12) будет: где ū_i, w, j - амплитуда, частота и фаза колебания, подставив которые в дифференциальные уравнения (5.12), получим систему однородных линейных алгебраических уравнений относительно неизвестных амплитуд колебаний ū_k:

(5.13)

где , а - символ Кронекера, равный единице, если i=k, и равный нулю, если i¹ k (i=1,2,…,n).

Вводя обозначение , (5.14)

перепишем (5.14) в виде:

, (5.15)

Условие разрешимости системы уравнений (5.15) состоит в равенстве нулю определителя n -го порядка. Определитель (5.16) представляет собой уравнение n -й степени относительно l и называется вековым уравнением, корни которого l_i дают n частот колебаний .

= 0 (5.16)

Подставив корень в систему (5.15) и решив эту систему однородных линейных уравнений, получим амплитуды колебаний (дополнительный индекс указывает на соответствие с данным значением ). При этом частное решение (5.13) уравнения (5.12) примет вид:

, . (5.17)

Колебательное движение, описываемое системой равенств (5.17), называется нормальным колебанием. Совокупность амплитуд 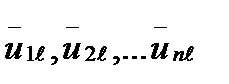определяет так называемую форму ℓ -го нормального колебания, дающую соотношение между изменениями естественных колебательных координат в ℓ -м нормальном колебании. Естественные S_i и нормальные координаты связаны простым соотношением:

,

причем нормальные координаты определены следующим образом:

.

Кинетическая и потенциальная энергия в нормальных координатах записываются в следующем виде:

; .

Соответствующие уравнения тоже приобретают достаточно простой вид. Несмотря на это, целесообразность перехода от естественных к нормальным координатам определяется целями и средствами исследования и не решается однозначно.

На первом этапе решения рассматриваемой задачи переход к нормальным координатам не осуществлялся, т.к. в данном случае представляется привлекательной ясность физического истолкования естественных координат.

На заключительном этапе определяются амплитуды вынужденных колебаний различных частей экскаватора. На данном этапе определяется зависимость амплитуд от частоты внешней возмущающей силы. В этом случае уравнения движения c использованием матричной формы [59] записываются в виде:

(5.18)

где F_i(t) - возмущающая сила, соответствующая перемещению S_i,;

m_i,j – матрица инерционных коэффициентов;

Rij - матрица Релея [59], определяющая трение в системе;

k_i,j – матрица силовых коэффициентов.

Элементы матрицы R_ij выбираются на основе имеющихся экспериментальных и литературных данных.

В рамках метода комплексных амплитуд [59, 168] решение уравнения (5.18) отыскиваем в виде:

(5.19)

Также как в (5.17) колебательное движение, описываемое системой равенств (5.19), называется нормальным колебанием.

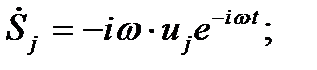
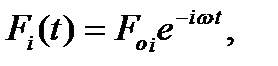Первая и вторая производные функции (5.19), соответственно равны: Полагая, что подставляем производные в (5.18), получаем систему линейных алгебраических уравнений относительно амплитуд u_j:

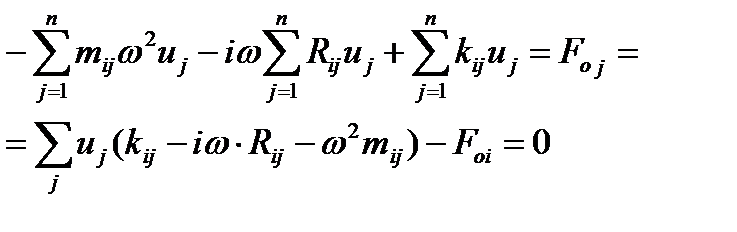, (5.20)

,

где u_j - комплексная амплитуда, определяющая как действительную амплитуду, так и фазу колебаний элементов и узлов экскаватора.

Решая (5.20) находим:

(5.21)

где D(ω) – детерминант, составленный из коэффициентов при u_j, а D_j(ω) – получается из D(ω) посредством замены j -го столбца на F_о1…F_оn..

Нас будет интересовать знаменатель дроби (5.21), так как именно им определяется резонансная характеристика системы. Поскольку он представляет детерминант векового уравнения, то его можно записать в виде:

, (5.22)

где ω_1…ω₂…ω_n – собственные частоты свободных колебаний, а G - некоторая постоянная.

Это выражение можно представить также в виде:

.

Для разделения вещественной и мнимой части u_j помножим знаменатель (5.21) на комплексно сопряженное выражение знаменателя D^*(ω). Тогда новый знаменатель будет равен:

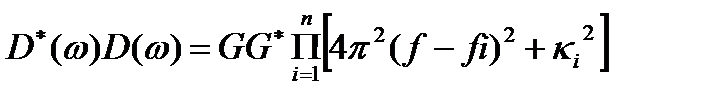, (5.23)

откуда видно, что резонанс будет возникать, когда частота f будет совпадать с одной из собственных частот свободных колебаний f_i. Однако вследствие наличия постоянных κ_i знаменатель (5.23) уже не будет обращаться в нуль. Это связано с тем, что возмущающая сила теперь совершает работу против сил трения, и резонансные амплитуды уже не будут бесконечными.

Используя данный математический аппарат, проведем теоретические исследования колебаний основных масс экскаватора, задавшись основными инерционными коэффициентами - m_ij, диссипативными - R_ij с выводом зависимостей для вычисления силовых коэффициентов - k_ij. Для этого разработаем динамическую модель, алгоритмы и программное обеспечение к решению полученных уравнений, описывающих системы с многими степенями свободы.

5.2. Динамическая модель колебаний карьерного экскаватора,