Течение неньютоновских жидкостей

Течение жидкостей под нагрузкой является предметом изуче­ния науки о деформациях и течении — реологии.

В предыдущих разделах рассматривались законы движения жидкостей, подчиняющихся закону внутреннего трения Ньютона. Вязкость этих жидкостей остается постоянной при дан­ной температуре и давлении. В отличие от них вязкость неньюто­новских жидкостей не постоянна, а изменяется в зависимости от скорости сдвига, его продолжительности, т. е. «предыстории» жидкости. В технологии строительных материалов к таким жидкостям относятся цементные шламы и растворы, бетонная смесь, глиняные шликеры и пасты, растворы полимеров, краски и т. п. Графики, вы­ражающие зависимость изменения предельного напряжения сдвига от градиента скорости, носят название кривых течения.

В современной теории неньютоновские жидкости подразделяют на три класса.

К первому классу относятся вязкие или стационарные ненью­тоновские жидкости, для которых в уравнении у = f(dv/dх) функция не зависит от времени.

По виду кривых течения различают бингамовские (рис. 4.3 ), псевдопластичные и дилатантные жидкости.

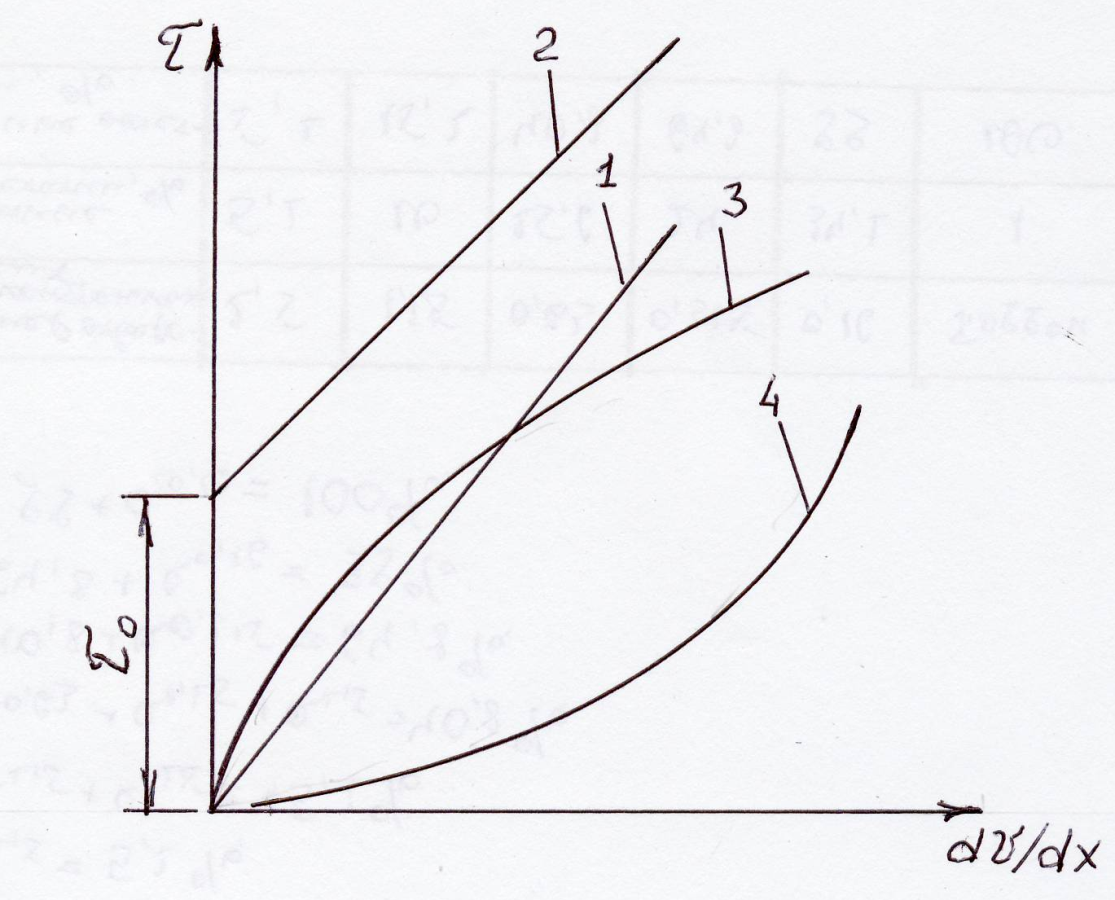
Рис. 4.3. Кривые течения жидкостей под нагрузкой: 1 – ньютоновская; 2 – бингамовская; 3 – псевдопластичная; 4 – дилатанатная

Течение бингамовской жидкости начинается только после при­ложения τ₀ (подсчитанного по уравнению Ньютона), которое необходимо для разрушения структуры, образовавшейся в данной системе. Такое течение называют пластическим, а критическое (т. е. предельное) напряжение сдвига τ₀ — пределом текучести. При на­пряжениях, меньших τ₀, бингамовские жидкости ведут себя как твердые тела, а при напряжениях, больших τ₀ — как ньютоновские жидкости, т. е. зависимость τ₀ от dv/dх линейна.

Считается, что структура тела Бингама под действием предель­ного напряжения сдвига мгновенно и полностью разрушается, в результате чего тело Бингама превращается в жидкость, при сня­тии напряжения структура восстанавливается и тело возвращается к твердому состоянию. Такое свойство жидкости (материала) называется тиксотропией.

Уравнение кривой течения 2 носит название уравнения Шведова -

Бингама

τ = τ₀ + η_пл(dv/dх), (4.9)

где η_пл — пластическая вязкость постоянна и аналогична вязкости обычной жидкости.

Для большинства структурированных систем зависимость dv/dх от τ не выражается прямой, а представляется кривыми (рис. 4.3, кривые 3,4).

Нарушения структуры в этой области столь незначительны, что успевают восстанавливаться в самом процессе течения.

К псевдопластичным жидкостям относятся растворы полиме­ров, целлюлозы и суспензии с асимметричной структурой частиц (кривая 3). К дилатантным жидкостям (кривая 4 ) относятся суспен­зии крахмала, различные клеи с большим отношением Т/Ж. В от­личие от псевдопластических эти жидкости характеризуются воз­растанием кажущейся вязкости с увеличением градиента скорости.

В зависимости от характера влияния продолжительности сдвига
на структуру различают тиксотропные и реопектантные жидкости.
У тиксотропных жидкостей с увеличением продолжительности
воздействия напряжения сдвига определенной ве­личины структура разрушается, вязкость уменьшается, а теку­честь возрастает. После снятия напряжения структура жидко­сти постепенно восстанавлива­ется с увеличением вязкости. Типичным примером тиксотроп­ных жидкостей являются мно­гие краски, увеличивающие вязкость со временем. У реопектических жидкостей с увеличением продолжительности воздействия напряжения сдвига текучесть сни­жается (структура упрочняется). К этим жидкостям относятся суспензии бентонитовых глин и не­которые коллоидные растворы.

К третьему классу относятся вязкоупругие или максвелловские жидкости. Жидкости текут под действием напряжения т, но после снятия напряжения частично восстанавливают свою форму. Таким образом, эти структуры обладают двойным свойством — вязким те­чением по закону Ньютона и упругим восстановлением формы по закону Гука. Примером их служат некоторые смолы и пасты, крах­мальные клеи.

Date: 2015-10-21; view: 2477; Нарушение авторских прав