
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Организация материально-технического снабжения
|
|
производства (закупок сырья)
Содержательная постановка задачи. Для производства товара используется сырье, потребность в котором определяется производственной программой.
В зависимости от объемов и сроков поставок партий сырья, типа груза и требований, предъявляемых к нему, а также надежности поставок, осуществляется выбор вида транспорта по критерию минимума совокупных затрат в процессе товародвижения.
Для выбора моментов предъявления заказов на пополнение запасов сырья выбирается динамическая модель в виде процесса с периодом, равным году и временным интервалом, равным 12 /m, с учетом динамики расходования сырья и изменения стоимостных параметров во времени.
Математическая постановка задачи. Обозначим через 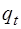 - объем поставки сырья в момент времени t, т;
- объем поставки сырья в момент времени t, т; 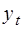 - расход данного вида сырья на складе в момент времени t, т; Gt - затраты на доставку партии заказа, р.;
- расход данного вида сырья на складе в момент времени t, т; Gt - затраты на доставку партии заказа, р.; 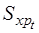 - затраты на хранение единицы запаса в единицу времени, р./т;
- затраты на хранение единицы запаса в единицу времени, р./т; 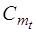 - стоимость 1 т груза, р.;
- стоимость 1 т груза, р.;  - удельные затраты на проведение погрузочно-разгрузочных работ, р./т.
- удельные затраты на проведение погрузочно-разгрузочных работ, р./т.
Тогда суммарные затраты в единицу времени, которые необходимо свести к минимуму, определятся из выражения:
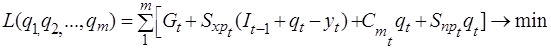
при ограничениях:
· на вместимость хранилищ склада
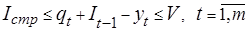 ; (3.7)
; (3.7)
· по загрузке транспортных средств
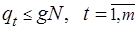 ; (3.8)
; (3.8)
· на неотрицательность переменных
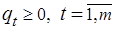 ; (3.9)
; (3.9)
где 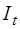 - текущий уровень запасов сырья на складе потребителя в момент времени t, т;
- текущий уровень запасов сырья на складе потребителя в момент времени t, т;  - максимальная вместимость склада, т;
- максимальная вместимость склада, т; 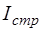 - страховой уровень запасов для обеспечения бесперебойной работы предприятия на случай возможной задержки поставки, т;
- страховой уровень запасов для обеспечения бесперебойной работы предприятия на случай возможной задержки поставки, т; 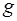 - вместимость одного автомобиля заданной грузоподъемности для доставки сырья потребителю, т;
- вместимость одного автомобиля заданной грузоподъемности для доставки сырья потребителю, т; 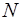 - количество автомобилей для перевозки сырья потребителю.
- количество автомобилей для перевозки сырья потребителю.
Для снижения затрат на доставку перевозка заказанного сырья производится целым количеством автомобилей.
В модели учитываются также скидки с цены на продукцию, зависящие от объемов поставки. Используя систему скидок, оптовую цену на сырье можно описать выражением:
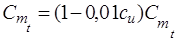 при au £ qt £ bu, u =
при au £ qt £ bu, u = 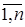 , (3.10)
, (3.10)
где n – общее число диапазонов объемов поставок, где действует скидка; 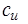 - скидка с оптовой цены (%), которая действует в диапазоне от минимального
- скидка с оптовой цены (%), которая действует в диапазоне от минимального  до максимального
до максимального 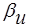 объема поставки.
объема поставки.
Данная задача также может быть решена методом динамического программирования. Обозначим через  суммарные затраты за периоды с 1 по t при оптимальной политике поставок сырья. Тогда оптимальное решение можно получить с помощью рекуррентных соотношений
суммарные затраты за периоды с 1 по t при оптимальной политике поставок сырья. Тогда оптимальное решение можно получить с помощью рекуррентных соотношений
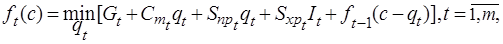 (3.11)
(3.11)
где  , (3.12)
, (3.12)
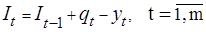 , (3.13)
, (3.13)
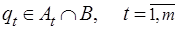 ; (3.14)
; (3.14)
 (3.15)
(3.15)
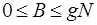 . (3.16)
. (3.16)
Начальные условия:  .
.
Пример. Потребность в сырье за год зависит от производственной программы, представленной в табл. 3.4. Для доставки сырья используются автомобили грузоподъемностью g = 10 т. Количество их не ограничено. Емкость склада  составляет 250 т. Текущий запас на складе на момент начала наблюдения I 0 равен 50 т. Страховой запас
составляет 250 т. Текущий запас на складе на момент начала наблюдения I 0 равен 50 т. Страховой запас 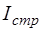 составляет 5 т. Задержки поставки отсутствуют. Исходные данные по транспортным тарифам
составляет 5 т. Задержки поставки отсутствуют. Исходные данные по транспортным тарифам 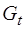 , стоимости товара
, стоимости товара 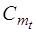 , затратам на хранение
, затратам на хранение 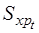 и погрузочно-разгрузочные операции
и погрузочно-разгрузочные операции 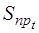 , меняющиеся в течение года, приведены в табл. 3.5.
, меняющиеся в течение года, приведены в табл. 3.5.
|
| |||||||||||||||||||||||||||||||||||||||
объемы поставок сырья в течение года. Суммарный спрос за год, в соответствии с табл. 3.4, составляет  = 195 т. Так как поставки осуществляют полностью загруженными автомобилями, то данная сумма должна делиться нацело на 10, т.е. границы изменения для
= 195 т. Так как поставки осуществляют полностью загруженными автомобилями, то данная сумма должна делиться нацело на 10, т.е. границы изменения для 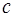 от 0 до 200 т с шагом 10 т.
от 0 до 200 т с шагом 10 т.
Для 1-го периода: I 1 = I 0 – y 1 + q 1 = 50 – 35 + q 1= 15 + q 1 > Iстр = 5. Максимальное поступление сырья составляет 200 т. Имеем: (200 + 15 = 215 < V = 250 т), т.е. неравенство (3.7) на этом этапе выполняется полностью.
При с = 0 и q 1 = 0 получаем:
f 1(0 -0) = G 1(0) + 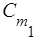 . 0 +
. 0 +  . 0 +
. 0 + 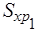 .I 1 + f 0(0 – 0) = 0+0+0+41,14.15+0 = 617,1 р.
.I 1 + f 0(0 – 0) = 0+0+0+41,14.15+0 = 617,1 р.
Для с = 0 – это единственные значения f 1(c) и q 1, поэтому они должны быть признаны оптимальными.
При 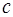 = 10 и q 1 = 0значение f 1(10 - 0) будет равно f 1(0 - 0) и составит также 617,1 р. Аналогично будет обстоять дело и для всех остальных с, т.е. f 1(0 - 0) = = f 1(10-0) = f 1(20 - 0) = … = f 1(200 - 0) = 617,1 р.
= 10 и q 1 = 0значение f 1(10 - 0) будет равно f 1(0 - 0) и составит также 617,1 р. Аналогично будет обстоять дело и для всех остальных с, т.е. f 1(0 - 0) = = f 1(10-0) = f 1(20 - 0) = … = f 1(200 - 0) = 617,1 р.
При формировании партии поставки в 10 т можно использовать 1 автомобиль, и предоставляется скидка с цены в размере 2%, поэтому при с = 10 и q 1= 10 имеем: f 1(10 - 10) = G 1(10) + (1 – 0,01.2) 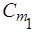 . 10 +
. 10 +  . 10 +
. 10 + 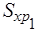 .I 1 + f 0(10 – 10) = 894,5.1 + +0,98 .375,5.10 + 20,50.10 + 41,14(15 + 10) + 0 = 5807,9р.
.I 1 + f 0(10 – 10) = 894,5.1 + +0,98 .375,5.10 + 20,50.10 + 41,14(15 + 10) + 0 = 5807,9р.
Так как должно быть выбрано минимальное для данного с значение, то имеем 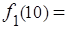 617,1р. и
617,1р. и  0. Аналогично проводятся расчеты для всех
0. Аналогично проводятся расчеты для всех 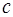 и q 1 в пределах 1-го периода. Полученные данные приведены в табл. 3.6.
и q 1 в пределах 1-го периода. Полученные данные приведены в табл. 3.6.
Значения 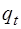 , соответствующие минимальным значениям f 1(c) для всех
, соответствующие минимальным значениям f 1(c) для всех 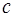 от 0 до 200 составляют
от 0 до 200 составляют 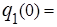
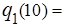
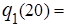 … =
… = 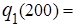 0, т.е. q 1 = 0 является оптимальным значением партии поставки в 1-ом периоде.
0, т.е. q 1 = 0 является оптимальным значением партии поставки в 1-ом периоде.
При расчетах для 2-го периода имеем: I 2 = I 1 – y 2 + q 2 = 15 – 35 + q 2 = - 20 + q 2. При отсутствии поставки на этом этапе (q 2= 0), равно как и при поставках q 2 = 10 т и q 2 = 20 т, запас оказывается меньше гарантированного (- 20 < 5; - 10 < 5; 0 < 5), а
Таблица 3.6
Значения функции f 1(c)
| t | с | q 1 | f 1 (c) | t | c | q 1 | f 1 (c) | t | c | q 1 | f 1 (c) |
| 617,1 | … | … | … | … | 69082,7 | ||||||
| 617,1 | 35638,5 | 617,1 | |||||||||
| 5807,9 | 40641,5 | 5807,9 | |||||||||
| 617,1 | 617,1 | … | … | … | … | ||||||
| 5807,9 | 5807,9 | 69082,7 | |||||||||
| 10923,6 | … | … | … | … | 73973,1 | ||||||
| 617,1 | 40641,5 | 617,1 | |||||||||
| 5807,9 | 44630,7 | 5807,9 | |||||||||
| 10923,6 | 617,1 | … | … | … | … | ||||||
| 15851,6 | 5807,9 | 73973,1 | |||||||||
| 617,1 | … | … | … | … | 78863,5 | ||||||
| 5807,9 | 44630,7 | 617,1 | |||||||||
| 10923,6 | 49521,1 | 5807,9 | |||||||||
| 15851,6 | 617,1 | … | … | … | … | ||||||
| 20929,7 | 5807,9 | 78863,5 | |||||||||
| 617,1 | … | … | … | … | 83753,9 | ||||||
| 5807,9 | 49521,1 | 617,1 | |||||||||
| … | … | … | … | 54411,5 | 5807,9 | ||||||
| 20929,7 | 617,1 | … | … | … | … | ||||||
| 25632,4 | 5807,9 | 83753,9 | |||||||||
| 617,1 | … | … | … | … | 88644,3 | ||||||
| 5807,9 | 54411,5 | 617,1 | |||||||||
| … | … | … | … | 59301,9 | 5807,9 | ||||||
| 25632,4 | 617,1 | … | … | … | … | ||||||
| 30635,4 | 5807,9 | 88644,3 | |||||||||
| 617,1 | … | … | … | … | 93534,7 | ||||||
| 5807,9 | 59301,9 | 617,1 | |||||||||
| … | … | … | … | 64192,3 | 5807,9 | ||||||
| 30635,4 | 617,1 | … | … | … | … | ||||||
| 35638,5 | 5807,9 | 88644,3 | |||||||||
| 617,1 | … | … | … | … | 95534,7 | ||||||
| 5807,9 | 64192,3 | 98425,1 |
значит, предприятие начинает нести большие убытки от срыва плана производства. Будем считать, что при недостаточном количестве сырья предприятие несет убытки в 50 раз выше, чем составляет экономия от сокращения запасов. Имеем:
f 2(0 - 0) = f 2(10 – 0) = f 2(20 – 0) = … = f 2(200 – 0) = G 2(0) +  .0 +
.0 + 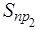 .0 + +
.0 + + 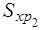 .I 2 + f 1(0 – 0) = 0 + 0 + 0 + 44,21.25.50 + 617,1 = 55879,6 р.
.I 2 + f 1(0 – 0) = 0 + 0 + 0 + 44,21.25.50 + 617,1 = 55879,6 р.
f 2(10 – 10) = f 2(20 – 10) = … = f 2(200 – 10) = 961,0.1 + 0,98. 403,5.10 + 20,56.10 + +44,21.15.50 + 5807,9 = 44086,3 р.
f 2(20 – 20) = f 2(30 – 20) = … = f 2(200 – 20) = 961,0.2 + 0,97. 403,5.20 + 20,56.20 + +44,21.5.50 + 10923,6 = 32137,2 р.
При поставке сырья в количестве 30 т ограничение (3.7) начинает выполняться (-20 + 30 = 10 > 5). Имеем:
f 2(30 - 30) = f 2(40 – 30) = … = f 2(200 – 30) = 961,0.3 + 0,95. 403,5.30 + 20,56.30 + +44,21.10 + 15851,6 = 31293,0 р.
f 2(40 - 40) = f 2(50 – 40) + … + f 2(200 – 40) = 961,0.4 + 0,95.403,5. 40 + 20,56.40 + +44,21.20 + 20929,7 = 41813,8 р.
Дальнейшее увеличение партии поставки приведет к росту функции f 2(с), поэтому на этом можно остановиться.
Минимальное значение функции f 2(c)для 2-го периода составляет 31293,0 р. и соответствует партии поставки q 2= 30 т, которая и должна быть признана оптимальной для этого этапа.
Аналогично просчитываются этапы с 3-го по 6-й. Результаты расчетов сведены в табл. 3.7.
Таблица 3.7
Значения функции 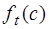
| t | с | qt | ft(c) | t |  c c
| qt | ft(c) | t | c | qt | ft(c) |
| 617,1 | 31293,0 | … | … |  … …
| … | ||||||
| 617,1 | 67438,6 | 87499,1 | |||||||||
| 617,1 | 67438,6 | 87499,1 | |||||||||
| 617,1 | … | … | … | … | 108373,8 | ||||||
  40 40
| 617,1 | 67438,6 | 108373,8 | ||||||||
| 617,1 |   110 110
| 67438,6 | … | … | … | … | |||||
| … | … | … | … | 67438,6 | 108373,8 | ||||||
| 617,1 | … | … | … | … |   170 170
| 108373,8 | |||||
| 31293,0 | 67438,6 | 108373,8 | |||||||||
| 31293,0 | 87499,1 | 108373,8 | |||||||||
| … | … | … | … | 87499,1 | 108373,8 | ||||||
| 31293,0 | … | … | … | … | 126298,7 | ||||||
  70 70
| 31293,0 | 87499,1 | … | … | … | … | |||||
| 31293,0 |   140 140
| 87499,1 | 126298,7 | ||||||||
| … | … | … | … | 87499,1 |  200 200
|  30 30
| 126298,7 |
Минимальные затраты при оптимальной политике поставок сырья составят f 6(200) = 126298,7 р. Используя данные табл. 3.7 и двигаясь в обратном направлении, т.е. от 6-го до 1-го периода, получим план поставок сырья на год. Например, функции f 6(200) по табл. 3.7 соответствует значение q 6 = 30 т. На следующих шагах принимается: f 5(200 - 30) и получаем q 5= 30 т, затем f 4(180 - 30) – q 4 = 30 ти т.д. Результаты расчетов при оптимальной политике поставок сырья приведены в табл.3.8.
Таблица 3.8
Результаты расчетов за год
| t | Спрос 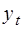 , т , т
| Текущий уровень запаса 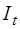 , т , т
| Объем поставки 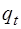 , т , т
| Затраты нарастающим итогом, р. |
| 617,1 | ||||
| 31293,0 | ||||
| 67438,6 | ||||
| 87499,1 | ||||
| 108373,8 | ||||
| 126298,7 |
Из табл. 3.8, следует, что поставки сырья автомобилями грузоподъемностью 10 т нужно осуществлять: по три – в апреле, августе, октябре и декабре, и четыре – в июне.
Date: 2015-10-19; view: 268; Нарушение авторских прав
 , р./т
, р./т
 , р./т
, р./т
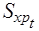 , р./т
, р./т