Описание метода измерений. Два физических маятника, имеющие общую горизонтальную ось вращения образуют замкнутую систему в момент прохождения ими положения равновесия (в этом положении

Два физических маятника, имеющие общую горизонтальную ось вращения образуют замкнутую систему в момент прохождения ими положения равновесия (в этом положении моменты сил тяжести равны нулю, а других моментов относительно оси вращения просто нет). Следовательно, при прохождении положения равновесия для этой системы выполняется закон сохранения момента импульса:

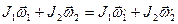
где J₁ и J₂ - моменты инерции маятников относительно оси вращения; 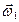и - и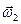х угловые скорости в положении равновесия до их соударения; 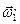и - и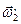х угловые скорости после взаимодействия.

До взаимодействия второй маятник покоится 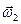= 0, а после взаимодействия оба маятника движутся как единое целое ( 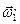= = 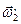ω) и поэтому закон сохранения момента импульса в проекции на ось вращения принимает вид:

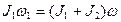
Моменты инерции маятников можно найти, зная их периоды колебаний

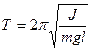
где l - расстояние от оси вращения до центра масс маятника.

Таким образом, момент инерции маятника 1

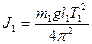(без добавочного груза);

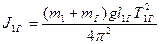(с грузом)

момент инерции системы из двух маятников

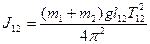(без груза)

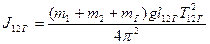(с грузом)

где l₁₂, l_12Г - расстояние от оси до центра масс системы из двух маятников без дополнительного груза и с грузом; Т₁₂, Т_12Г -период колебания системы из двух маятников (без груза и с грузом).

При отклонении маятника от положения равновесия на угол α центр масс его поднимется на высоту (рис. 8) h = l (1 – cos α).

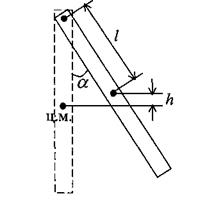
Рис. 8

Так как до взаимодействия и после взаимодействия на маятник действует только сила тяжести (консервативная), а момент силы сопротивления достаточно мал, из закона сохранения механической энергии

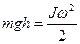
можно найти угловую скорость маятника в момент прохождения положения равновесия:

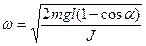
где энергия колеблющегося маятника при прохождении положения равновесия, mgh - энергия маятника, отклоненного на угол α (при этом его центр масс поднят на высоту h).

В наших опытах первоначально маятник 1 отклоняется от положения равновесия на угол α и, следовательно, его угловая скорость при прохождении положения равновесия (т.е. перед взаимодействием (столкновением) с маятником В)):

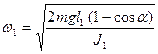(без добавочного груза);

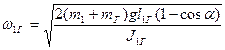(с грузом)

После столкновения система из двух маятников отклоняется на угол β и следовательно, их начальная угловая скорость в положении равновесия:

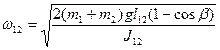(без добавочного груза);

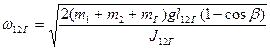(с грузом)

Date: 2015-10-19; view: 561; Нарушение авторских прав