
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчетные задания
|
|
Задание 1. Для матрицы третьего порядка вычислите ее определитель
и определитель матрицы, транспонированной к данной.
1.  ; 2.
; 2. 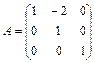 ; 3.
; 3. 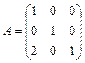 ;
;
4.  ; 5.
; 5. 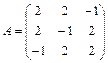 ; 6.
; 6. 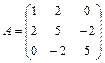 ;
;
7. 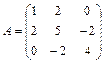 ; 8.
; 8.  ; 9.
; 9.  ;
;
10. 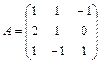 ; 11.
; 11. 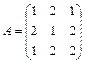 ; 12.
; 12. 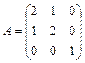 ;
;
13. 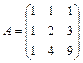 ; 14.
; 14. 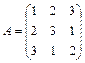 ; 15.
; 15.  ;
;
16. 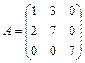 ; 17.
; 17.  ; 18.
; 18. 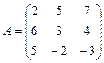 ;
;
19. 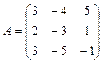 ; 20.
; 20. 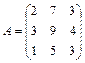 ; 21.
; 21.  ;
;
22. 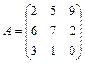 ; 23.
; 23.  ; 24.
; 24.  ;
;
25. 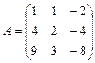 .
.
Задание 2. Вычислите определитель четвертого порядка
1. 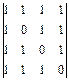 ; 2.
; 2.  ; 3.
; 3. 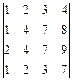 ;
;
4. 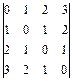 ; 5.
; 5. 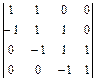 ; 6.
; 6. 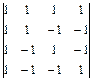 ;
;
7. 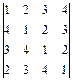 ; 8.
; 8. 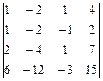 ; 9.
; 9.  ;
;
10.  ; 11.
; 11. 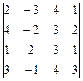 ; 12.
; 12. 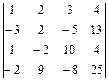 ;
;
13. 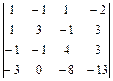 ; 14.
; 14.  ; 15.
; 15. 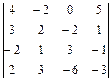 ;
;
16. 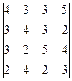 ; 17.
; 17.  ; 18.
; 18. 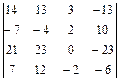 ;
;
19.  ; 20.
; 20. 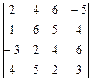 ; 21.
; 21. 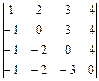 ;
;
22. 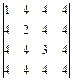 ; 23.
; 23. 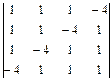 ; 24.
; 24. 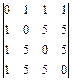 ;
;
25. 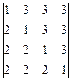 .
.
Задание 3. Найдите матрицу, обратную матрице. Проверьте результат,
вычислив произведение взаимно обратных матриц.
1.  ; 2.
; 2.  ;
;
3. 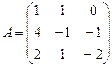 ; 4.
; 4.  ;
;
5. 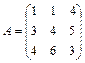 ; 6.
; 6. 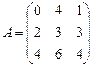 ;
;
7. 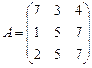 ; 8.
; 8.  ;
;
9. 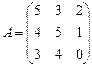 ; 10.
; 10. 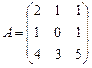 ;
;
11. 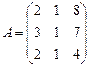 ; 12.
; 12. 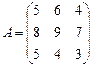 ;
;
13.  ; 14.
; 14.  ;
;
15. 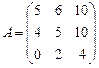 ; 16.
; 16. 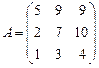 ;
;
17. 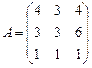 ; 18.
; 18. 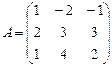 ;
;
19. 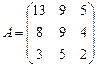 ; 20.
; 20.  ;
;
21.  ; 22.
; 22. 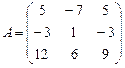 ;
;
23. 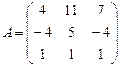 ; 24.
; 24.  ;
;
25. 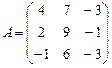 .
.
Задание 4. Решите систему линейных уравнений матричным способом.
1.  ; 2.
; 2. 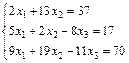 ;
;
3.  ; 4.
; 4.  ;
;
5. 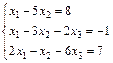 ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9. 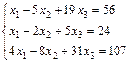 ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13. 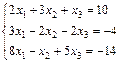 ; 14.
; 14. 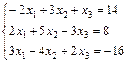 ;
;
15.  ; 16.
; 16. 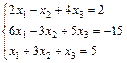 ;
;
17. 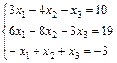 ; 18.
; 18. 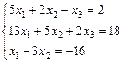 ;
;
19. 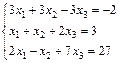 ; 20.
; 20. 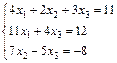 ;
;
21.  ; 22.
; 22. 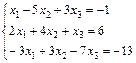 ;
;
23.  ; 24.
; 24. 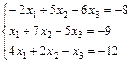 ;
;
25.  .
.
Задание 5. Решите систему линейных уравнений по формулам
Крамера.
1.  ; 2.
; 2. 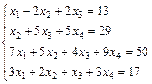 ;
;
3. 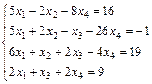 ; 4.
; 4. 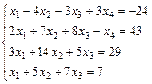 ;
;
5. 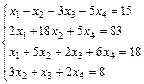 ; 6.
; 6. 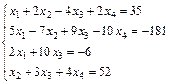 ;
;
7. 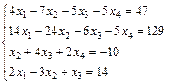 ; 8.
; 8. 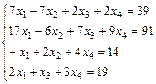 ;
;
9.  ; 10.
; 10. 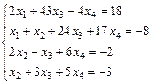 ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14. 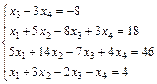 ;
;
15.  ; 16.
; 16. 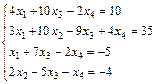 ;
;
17. 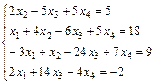 ; 18.
; 18. 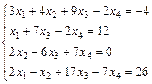 ;
;
19. 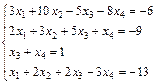 ; 20.
; 20. 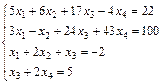 ;
;
21.  ; 22.
; 22.  ;
;
23. 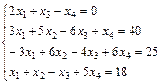 ; 24.
; 24. 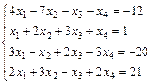 ;
;
25.  .
.
Задание 6. Примените теорему Кронекера-Капелли и найдите все решения системы методом Гаусса.
1. 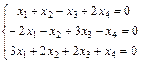 ; 2.
; 2. 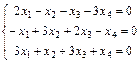 ;
;
3. 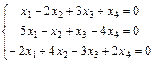 ; 4.
; 4.  ;
;
5. 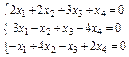 ; 6.
; 6. 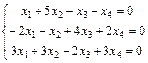 ;
;
7. 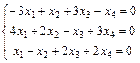 ; 8.
; 8. 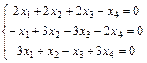 ;
;
9. 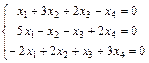 ; 10.
; 10. 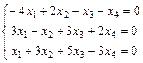 ;
;
11. 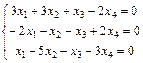 ; 12.
; 12. 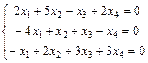 ;
;
13. 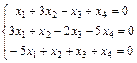 ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17. 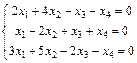 ; 18.
; 18. 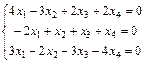 ;
;
19. 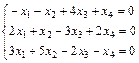 ; 20.
; 20. 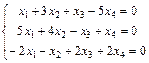 ;
;
21.  ; 22.
; 22. 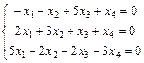 ;
;
23. 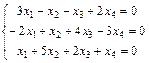 ; 24.
; 24. 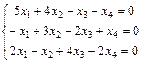 ;
;
25.  .
.
Задание 7. Дана расширенная матрица системы. Найдите решение этой
системы и соответствующей ей однородной системы.
1. 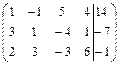 ; 2.
; 2. 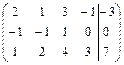 ;
;
3.  ; 4.
; 4. 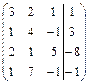 ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8. 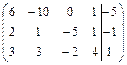 ;
;
9. 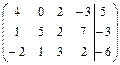 ; 10.
; 10.  ;
;
11. 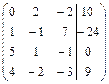 ; 12.
; 12.  ;
;
13. 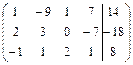 ; 14.
; 14.  ;
;
15. 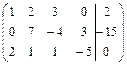 ; 16.
; 16. 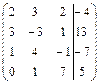 ;
;
17. 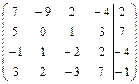 ; 18.
; 18. 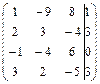 ;
;
19.  ; 20.
; 20.  ;
;
21. 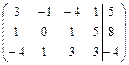 ; 22.
; 22.  ;
;
23. 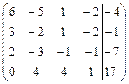 ; 24.
; 24. 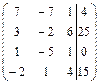 ;
;
25.  .
.
Задание 8. Даны координаты векторов а1, а2, а3, а4 и b в некотором базисе. Покажите, что векторы а1, а2, а3, а4 образуют базис и найдите координаты вектора b в этом базисе.
1. а1 (1,2,-1,-2); а2 (2,3,0,1); а3 (1,2,1,3); а4 (1,3,-1,0); b (7,14,-1,2).
2. а1 (2,1,0,-1); а2 (2,3,0,-2); а3 (2,4,2,1); а4 (0,-3,0,2); b (5,2,1,0).
3. а1 (1,1,4,2); а2 (2,-1,3,1); а3 (0,2,0,0); а4 (1,-1,0,1); b (5,0,0,5).
4. а1 (1,2,3,4); а2 (2,3,4,1); а3 (3,4,1,2); а4 (4,1,2,3); b (2,2,2,4).
5. а1 (2,0,0,0); а2 (0,4,0,0); а3 (0,0,6,0); а4 (0,0,0,8); b (6,7,0,1).
6. а1 (1,2,-1,-2); а2 (2,3,0,1); а3 (1,2,1,3); а4 (1,3,-1,0); b (6,7,0,1).
7. а1 (2,1,0,-1); а2 (2,3,0,-2); а3 (2,4,2,1); а4 (0,-3,0,2); b (-3,2,5,0).
8. а1 (2,3,4,5); а2 (3,4,5,2); а3 (4,5,2,3); а4 (5,2,3,4); b (-1,2,1,-2).
9. а1 (3,5,-1,-1); а2 (3,5,1,4); а3 (2,5,0,3); а4 (1,3,-1,0); b (7,14,-1,2).
10. а1 (4,4,0,-3); а2 (4,7,2,-1); а3 (2,1,2,3); а4 (0,-3,0,2); b (5,2,1,0).
11. а1 (3,0,7,3); а2 (2,1,3,1); а3 (1,1,0,1); а4 (1,-1,0,1); b (5,0,0,5).
12. а1 (3,5,7,5); а2 (5,7,5,3); а3 (7,5,3,5); а4 (4,1,2,3); b (2,2,2,4).
13. а1 (2,4,0,0); а2 (0,4,6,0); а3 (0,0,6,8); а4 (0,0,0,8); b (-14,6,0,1).
14. а1 (1,2,-1,-2); а2 (3,5,-1,-1); а3 (3,5,1,4); а4 (2,5,0,3); b (6,7,0,1).
15. а1 (2,1,0,-1); а2 (4,4,0,-3); а3 (2,7,2,-1); а4 (2,1,2,3); b (-3,2,5,0).
16. а1 (5,7,9,7); а2 (7,9,7,5); а3 (9,7,5,7); а4 (5,2,3,4); b (-1,2,1,-2).
17. а1 (1,3,5,3); а2 (3,5,3,2); а3 (5,3,1,3); а4 (3,0,1,2); b (-6,0,2,-3).
18. а1 (-1,1,3,1); а2 (1,3,1,-1); а3 (3,-1,-1,1); а4 (2,-1,0,1); b (-3,6,7,-2).
19. а1 (0,1,2,3); а2 (1,2,3,0); а3 (2,3,0,1); а4 (3,0,1,2); b (-6,0,2,-3).
20. а1 (-1,0,1,2); а2 (0,1,2,-1); а3 (1,2,-1,0); а4 (2,-1,0,1); b (-3,6,7,-2).
21. а1 (4,4,3,0); а2 (-17,24,1,1); а3 (-6,-1,2,0); а4 (-5,3,1,0); b (-9,10,1,1).
22. а1 (2,2,7,7); а2 (-9,-7,-6,-17); а3 (-4,-2,2,1); а4 (-3,-1,0,2); b (-15,-7,17,14).
23. а1 (2,4,2,1); а2 (-10,-9,-7,-5); а3 (0,10,0,-2); а4 (-4,3,-1,0); b (-42,-43,-39,23).
24. а1 (3,3,4,1); а2 (-1,-8,-7,2); а3 (0,5,14,-3); а4 (0,1,5,-1); b (9,31,34,-5).
25. а1 (8,3,2,5); а2 (-26,1,2,-5); а3 (4,2,1,6); а4 (-2,1,0,2); b (14,17,12,27).
Теоретические вопросы, выносящиеся на защиту
- Матрицы и действия над ними.
- Определитель. Свойства. Вычисление.
- Обратная матрица.
- Матричный способ решения систем линейных уравнений.
- Метод Крамера.
- Метод Гаусса.
- Линейное пространство. Арифметическое пространство.
- Евклидово пространство.
Список литературы
1. Выгодский М.Я. Справочник по высшей математике. –М.:Наука, 1975.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1.-М.:Выс. школа, 1986.
3. Клетеник Д.В. Сборник задач по аналитической геометрии.-М.:Наука, 1986.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления. –М.:Наука, 1978.
5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа /Под ред. А.В.Ефимова, Б.П.Демидовича. – М.:Наука, 1981.
Содержание
| 1. Определители и их вычисления …………………………………. | |
| 2. Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса ……………………. | |
| 3. Примеры …………………………………………………………… | |
| 4. Расчетные задания ………………………………………………... | |
| Список литературы ………………………………………………… |
Редактор Л.А.Матвеева
Подписано в печать 7.07.05. Бумага офсетная. Формат 60х84 1/16.
Гарнитура “Таймс”. Печать трафаретная. Усл.-печ.л. 1,6. Уч.-изд.л. 1,4
Тираж 100 экз. Заказ
Издательство Уфимского государственного нефтяного технического университета
Адрес издательства:
450062, РБ, г.Уфа, ул.Космонавтов, 1.
Date: 2015-10-19; view: 366; Нарушение авторских прав