
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Матричный метод решения системы линейных алгебраических уравнений. Формулы Крамера. Метод Гаусса
|
|
Рассмотрим систему, составленную из трех линейных алгебраических уравнений с тремя неизвестными.
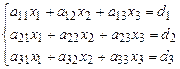 (2.1)
(2.1)
Решением (2.1)называется система 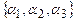 из трех чисел, удовлетворяющая требованию: если в (2.1) вместо
из трех чисел, удовлетворяющая требованию: если в (2.1) вместо 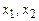 и
и 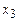 подставить соответственно
подставить соответственно 
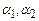 и
и 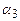 , то получим три верных равенства (три тождества).
, то получим три верных равенства (три тождества).
 (2.2)
(2.2)
- основная матрица системы (2.1)
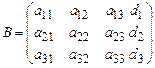 (2.3)
(2.3)
- расширенная матрица (2.1)
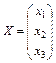 ;
; 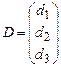 ;
; 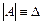 (2.4)
(2.4)
система (2.1) может быть записана в матричном виде так:
AX=D (2.5)
X – неизвестная матрица-столбец. Введем вспомогательные определители:
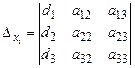
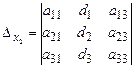
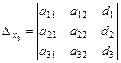
Предполагая, что матрица A - невырожденная и умножая (2.5) слева и почленно на A-1, получим
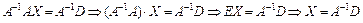 – (2.6) матричный способ решения системы.
– (2.6) матричный способ решения системы.
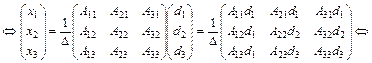
Используя понятие равенства двух матриц, получим
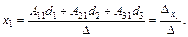 (2.7)
(2.7)
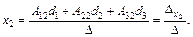 (2.8)
(2.8)
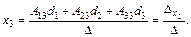 (2.9)
(2.9)
Элементарными преобразованиями матрицы называются следующие преобразования:
- Перестановка местами произвольных двух строк (столбцов).
- Умножение строки (столбца) на отличное от нуля число.
- Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число.
Date: 2015-10-19; view: 325; Нарушение авторских прав