Расчет критерия χ 2

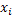
№	Классовая варианта.	Частоты.	Разность.	Квадрат диаметра. d2	χ 2
эмп.	теор.

Оценка степени соответствия производится по сумме значений колонки 7.

По таблице №4 приложений для соответствующего уровня доверительной вероятности и по числу степеней свободы вариационного ряда выбирает табличное значение (χ²). Если табличное (χ²) меньше фактического, то признаётся соответствие эмпирического и теоретического распределений. Число степеней свободы рассчитывается от количества классов минус 3 (m = 5 – 3= 2). При составлении таблицы 18 следует иметь в виду, что при вычислении χ² частоты крайних классов ВР не должны быть менее 5.

Раздел 5. Расчет показателей связи в выборочной совокупности и их оценка.

В разбираемом нами примере были исследованы два признака: диаметр и высота. Получены статистические характеристики их ВР. На их основе можно приступить к количественной оценке связи между этими признаками. Сделать это можно двумя методами: используя корреляционный анализ или связанный с ним регрессионный анализ. В рамках контрольной работы выполняется оба вида анализа связи.

Корреляционный анализ начинают с построения так называемой корреляционной решетки – такой таблицы, в которой сопряжены два изучаемых признака в виде уже известных ВР.

Таблица 19.

	Корреляционная решетка.
	3	2
	1	2	1
		3	2	1
		1	10	4
			3	4	5	2
				2	1	1	1
							1
nx
	9,75	13,12	17,12	19,91	21,50	22,0	25,5

Характер распределения частот по сопряженным вариационным рядам уже позволяет сделать определенные выводы о наличии связи. Диагональное распределение частот от меньших значений вариант к большим по обоим ВР дает первую характеристику связи, которая называется направленностью. В данном случае она положительная: увеличению диаметров соответствует увеличение частот. Кроме того, распределение частот по клеткам корреляционной решетки вскрывает смысл корреляционного анализа. Он устанавливает зависимость средних значений одного варьирующего признака (высоты в данном случае) от фиксированных значений другого (диаметра).

Следующая характеристика связи между изучаемыми предметами – ее теснота. Теснота связи характеризуется числовым значением коэффициента корреляции:

(25)

где: r – коэффициент корреляции.

– произведение отклонений классовых вариант по диаметру и по высоте с учетом частоты по каждой клетки решетки.

Величины коэффициента корреляции лежит в пределах -1 - +1. Знак перед r характеризует направленность связи. Абсолютная величина r показывает тесноту или силу взаимосвязи признаков. До 0,3 – связь практически отсутствует, от 0,3 до 0,5 – связь слабая, 0,5-0,7 – средняя, 0,7-0,9 – сильная. Свыше 0,9 – практически функциональная.

Форма связи между исследуемыми признаками, кроме ее визуальной оценки по корреляционной решетке, может быть охарактеризована более определенно по значению так называемого коэффициента криволинейности.

(26)

где: - корреляционное отношение.

r – коэффициент корреляции.

Корреляционное отношение – аналог коэффициента корреляции, причем более универсальный: применим для любой формы связи. Рассчитывается по формуле:

(27)

где: - частное среднее значение высоты по классам x (диаметр) с учетом суммарной частоты класса () в корреляционной решетке.

Символ обозначает оценку связи y по x, то есть высоты в зависимости от диаметра, на что указывает индекс. По существу корреляционное отношение устанавливает долю частной дисперсии по y (высоте) в общей дисперсии.

Ошибка коэффициента криволинейности рассчитывается по формуле:

(28)

Вывод о форме связи делается на основании нулевой гипотезы () в предположении, что () = 0, то есть связь прямолинейна.

(29)

Тогда при нулевая гипотеза принимается, то есть форма связи близка к прямолинейной. При 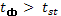нулевая гипотеза отвергается, связь является криволинейной.

Доверительная оценка коэффициента корреляции производится по критерию Стьюдента:

(30)

Предварительно следует рассчитать ошибку r:

(31)

Нулевая гипотеза отвергается, если (для степени свободы n-2) при принятом уровне доверительной вероятности.

Доверительная оценка корреляционного отношения производится точно так же, только вместо r в формуле стоит ɳ.

Интервальная оценка как коэффициента корреляции, так и корреляционного отношения производится по формулам:

(32)

Таким образом, в рамках корреляционного анализа получены три характеристики связи: теснота, форма и направленность. В КР следует более тщательно отнестись к понятию «теснота». В общем плане – это степень сопряженного варьирования признаков. Однако, общее поле варьирования двух признаков включает в себя точки, отражающие разную степень зависимости двух признаков, в том числе такие значения зависимого признака (высота) которые лишь формально связаны с диаметрами, а на самом деле определяются суммарным влиянием других не учитываемых в опыте факторов. Отсюда следует, что коэффициент корреляции в той или иной степени преувеличивает оценку тесноты связи. Для того, чтобы исключить влияние случайных факторов(возможно, просто не учитываемых) на величину зависимого признака рассчитывается так называемый коэффициент детерминации.

d= r²

Значение d показывает долю значений признака, величина которых определяется преимущественно влиянием изменчивости диаметра. Например, если d=0,67, то это значит, что для 67% объема зависимого признака изменчивость определяется преимущественно изменчивостью факторного признака.

5. Регрессионный анализ.

В рамках регрессионного анализа, дополнительно характеристикам связи, полученным в корреляционном анализе, разработан способ оценки, который показывает на сколько изменяется, в среднем, зависимый признак при изменении независимого на одну единицу.

В корреляционном анализе установлена форма связи между признаками. Для установленной формы выбирают соответствующее уравнение общего вида. Допустим, что это уравнение прямой: y= a + bx.

В регресионом анализе исследуемые признаки подразделяют на результативный признак (признак-функцию) и факторный признак (признак аргумент). В нашем случае результативный признак – это высота (y), а факторный - диаметер(x).

Графический способ отражения связи.

По определению регрессия устанавливает соотношение между средними значениями результативного признака и фиксированными значениями факторного. По данным корреляционной решетки строим соответствующую линию

Рис. Линия регрессии, эмпирическая.

Способ заключается в том, что «на глаз» производится «усреднение» точек разброса эмпирической линии. Усредненные точки соединяются плавной линией, в результате чего получается выровненная линия регрессии. Ее можно считать первым приближением к теоретической кривой, рассчитываемой аналитическими методами.

Способ скользящей средней.

Способ осуществляется следующим образом. Берутся три или более последовательных значений переменной (результативные): y₁ + y₂ + y₃, рассчитывается для x₂ (факультативного), далее находят среднее по сумме y₂ + y₃₊y₄. Это будет по x₃; и т.д.

Таким образом, среднее из соседних значений будет более точно отражать общую линию связи.

Способ наименьших квадратов.

Этот способ дает наиболее точную оценку связи. Он основан на требовании минимизации суммы квадратов отклонений от средней, т.е . Практически, в рамках контрольной работы, он реализуется следующим образом.

Каждая клетка корреляционной решетки содержит эмпирическую информацию о численном соотношении двух признаков (x – диаметр, y – высота), а также о количестве деревьев принадлежащих этому соотношению. То есть, по уже выбранному ранее общему виду уравнения связи можно построить столько эмпирических уравнений, сколько имеется заполненных клеток в корреляционной решетке. Например, из таблицы 19 для значений зависимого признака (x, y) соответственно 9 и 12(три и одно дерево в клетке), используя общий вид прямолинейной зависимости получаем:

(9=a+b*8)3

Далее таким же образом

(12=a+b*8)1

(15=a+b*12)3, и т.д.

Суммируя почленно эмпирические уравнения получаем в общем виде следующее уравнение:

(33)

Это первое уравнение системы, решая которую мы получим значения а и b, которые, собственно, и определят зависимость двух исследуемых признаков.

Второе уравнение получается после умножения каждого предыдущего уравнения на числовое значение независимой переменной (коэффициент при b).

Продолжая рассматривать наш пример, получим:

[(9=a+b*8)3]8

[(12=a+b*8)1]8

[(15=a+b*12)3]12 и т.д.

Суммируя почленно получим второе уравнение системы, общий вид которого таков:

(34)

Таким образом, построив два уравнения с двумя неизвестными и решая их как систему, найдем значения этих неизвестных

(35)

Тот же самый результат можно получить, прибегнув к математической формализации требования минимизации функции

(36)

Минимум функции достигается, как известно, после приравнивания к нулю её первой производной.

Уравнение (36) изменяем в развернутом виде

(37)

Находим частные производные функции y последовательно по a и b и приравниваем их к нулю.

(38)

После несложных преобразований получаем последовательно:

(39)

Таким образом, мы получим ту же систему нормальных уравнений, но несколько иным путем. Значения неизвестных из этой системы равны:

(40)

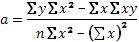
(41)

Для расчета этих же коэффициентов иногда удобно использовать следующие рабочие формулы:

(42)

(43)

Подставляя рассчитанные значения a и b в уравнение общего вида y=a+bx, получим эмпирическое уравнение связи двух признаков:

(44)

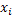По уравнению рассчитываем значение в зависимости от (значение классовых вариант в ВР по диаметру). Данные сводим в таблицу.

Таблица выровненных значений f(x).

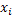
	x
	9,75	13,12	17,12	19,91	21,50	22,0	25,5

По приведенной таблице строим график установленной зависимости (формула). Следует совместить с эмпирической ломанной.

Рис. Эмпирическая линия связи по МНК.

Оценка репрезентативности установленной связи.

Коэффициенты в уравнении регрессии являются производными от исследуемых выборочных случайных величин. Следовательно, они сами являются величинами случайными и для них так же актуален вопрос: насколько рассчитанные значения соответствуют гипотетическим значениям генеральной совокупности.

Так же как и в предыдущих случаях, связанных с оценкой параметров, нужно рассчитать ошибку коэффициента регрессии (b):

(45)

где – - величина интервала по y

- величина интервала по x

Достоверность коэффициента регрессии оценивается по критерию t. При

(46)

Знание ошибки экспериментального коэффициента регрессии, позволяет установить доверительную зону случайных отклонений линии выборочной регрессии в пределах, обеспечивающих присутствие линии генеральной регрессии с принятой вероятностью.

При этом нулевая гипотеза () состоит в отрицании связи признаков, т.е. случай равенства нулю коэффициента регрессии.

Контрольная работа, выполненная по приведенной программе, является лишь одним из способов обработки исходной информации. В большинстве случаев как последовательность, так и методика анализа зависят от целевой установки экспериментатора, но, в любом случае, опыт обработки совокупности, приобретенный в данной работе будет несомненно полезен на любом этапе работы.