Раздел II. Расчет основных характеристик выборки

2.1. Характеристики, отражающие «центростремительные» тенденции.

Первая статистическая характеристика – это средняя арифметическая взвешенная, затем мода и медиана.

Все характеристики рассчитываются по вариационному ряду. Приведем его несколько в ином виде.

Вариационный ряд по диаметру (частоты и частости).

Таблица 3.

№	Интервал по диаметру	Срединное значение интервала (классовая варианта) xi (см)	Частота встречаемости классовой варианты ni (шт)	Частость классовой варианты (доля).
1.	6,0 – 10,0			0,06
2.	10,1 -14,0			0,16
3.	14,1 – 18,0			0,32
4.	18,1 – 22,0			0,24
5.	22,1 – 26,0			0,12
6.	26,1 – 30,0			0,06
7.	30,0 – 34,0			0,04
				1,0

Формула для расчета средней арифметической взвешенной

(1)

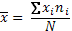
где: сумма значений классовых вариант, умноженных на соответствующие частоты, N = - объем выборки.

Другой расчет для определения средней основан на вероятностной природе выборки. Частости являются долями присутствия значений признака в общем объеме выборки, т.е. частями от общего объема, а значения отражают вероятность исхода испытания для значения признака (классовой варианты), связанного с этой частостью. Поскольку сумма частостей составляет полную группу событий, то среднее значение можно получить исходя из формулы (1)

(2)

Читается эта формула так: среднее значение случайной величины равно сумме произведений всех ее возможных значений на их вероятности.

Модой (Mo) называют варианту, которая имеет наибольшую частоту. В нашем примере она равна 16. В случае равных интервалов ее значение определяют по классовой варианте. Однако, в силу того, что в границах модального интервала имеет место разброс значений признака, а также сама частота интервала случайна и связана с частотами соседних классов, точное значение Mo рассчитывают по формуле:

(3)

где: Xo – нижняя граница модального класса,

K – величина интервала,

– частость модального класса.

– частость класса, предшествующего модальному.

– частость класса последующего за модальным.

Медианой (Me) называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. То есть в обе стороны от медианы находятся равные количества частот. Медиану вариационного ряда находят следующим образом:

1. Находим класс, которому принадлежит медиана. Для этого в ВР (таблица 2) рассматривают колонку накопленных частот. По значениям накопленных частот выбирают класс интервала. Первое значение накопленной частоты, которое больше половины объема выборки соответствует классу интервала, в котором присутствует медиана. В нашем примере первое значение накопленной частоты большее 1/2N (25) находится в третьем классе (27). Значит медиана находится в этом классе.
2. Находим значение медианы по формуле:

(3)

где: – нижняя граница класса интервала, содержащего медиану.

– накопленная частота, предшествующая медианному классу.

- частота медианного класса.

Отношение между средней арифметической, модой и медианой выражается формулой:

(4)

, откуда

(5)

Эти формулы справедливы для достаточно симметричных вариационных рядов_.

Необходимым условием симметричности ВР является равенство:

(6)

Нарушение приведенных соотношений свидетельствует о неравномерном распределении частот ВР относительно .

Для распределений с правосторонней асимметрией справедливо неравенство:

, с левосторонней - .

2.2. Характеристики изменчивости признака.

При построении ВР была использована разность между максимальной и минимальной величинами признака (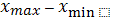). Эта разность называется размахом варьирования (изменчивости) и является одной из характеристик изменчивости. Размах варьирования – это, собственно, границы диапазона значений, применяемые признаком. Чем больше этот диапазон, тем сильнее варьирует признак.

Следующей рассчитываемой в работе характеристикой изменчивости является дисперсия. По определению – это средний квадрат отклонений от средней величины. Формула для ВР:

(7)

где: – последовательные слагаемые отклонения каждой классовой варианты от среднего значения ВР: .

– частота соответствующего класса интервала.

Если из значения дисперсии извлечь корень, то получается ещё одна характеристика изменчивости, которая называется средним квадратическим отклонением:

(8)

Дисперсию и, следовательно, среднеквадратическое отклонение можно вычислить также и по формуле:

(9)

,

где: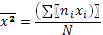

Размерность среднеквадратического отклонения такая же, как в исходных данных.

Перечисленные характеристики изменчивости признака – величины именованные. Это не всегда удобно, особенно, когда нужно сравнивать выборки с различной размерностью признака. Поэтому используется относительный показатель изменчивости, который называется коэффициентом вариации:

(10)

При величине коэффициента вариации примерно до 33% распределение можно считать достаточно однородным. Естественно, чем меньше V, тем совокупность однороднее. При V>50% использование этого коэффициента бессмысленно. Во всех случаях среднеквадратическое отклонение является более надежной оценкой изменчивости.

Еще один показатель изменчивости ряда распределения, тоже относительный, - нормированное отклонение:

(11)

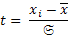
Нормированное отклонение производит оценку отклонения любой варианты от среднего значения ряда в размерности 𝔖. С помощью нормированного отклонения можно оценить положение каждой варианты в ряду распределения. Действительно, из формулы следует, что каждая варианта (x_i) связана с определенным значением t, которое указывает ее положение в ВР и на кривой распределения. В нашем примере, если пересчитать значения классовых интервалов в долях 𝔖, получим следующие t-распределение.

Таблица 4.

t -распределение диаметров по эмпирическим данным.

Это распределение показывает, что деревья с диаметром 8 находятся в левой части кривой полигона на расстоянии 1,87 𝔖 от . Деревья с диаметром 24 находятся от на расстоянии 0,98𝔖 в правой части полигона распределения и т.д.

2.3. Оценка формы эмпирического распределения.

Выборки, особенно малочисленные (<30ед.), как правило, по форме кривой распределения значительно отличаются от теоретической кривой нормального распределения.

Несимметричность эмпирического распределения можно оценить по характеру распределения частот в классах ВР. Графически она видна по форме полигона и гистограммы распределений. Количественная ее мера рассчитывается через специальные характеристики: асимметрия и эксцесс.

Асимметрия рассчитывается по формуле:

(12)

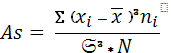
Если коэффициент равен нулю – ряд симметричен. Отрицательное значение As указывает не левостороннюю асимметрию, когда относительно модального класса левая часть кривой больше вытянута чем правая. Наоборот, когда более вытянута правая часть кривой распределения, говорят о правосторонней асимметрии. Коэффициент асимметрии не имеет ни верхней, ни нижней границы. Однако, на практике для умеренно асимметричных рядов он редко бывает больше единицы.

Коэффициент эксцесса характеризует форму вершины эмпирического распределения, он рассчитывается по формуле:

(13)

Положительное значение коэффициента эксцесса указывает на островершинность распределения. В этом случае классы с большими частотами группируются вокруг модального класса. Такого рода эксцесс называется положительным, а его коэффициент имеет знак «+». Положительный эксцесс не ограничен верхним пределом, но степень его соответствия нормальному распределению будет показана ниже. Отрицательное значение эксцесса указывает на плосковершинность распределения, имеет отрицательное значение, предельная величина которого равна – 2.

В заключение раздела приведем сводную таблицу, по которой удобно рассчитывать почти все приведенные выше статистические характеристики выборочной совокупности.

Таблица 14. Сводная таблица расчетов основных характеристик вариационного ряда.

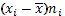
№	Классовая варианта	Частота	Отклонение	Отклонение с учетом частоты	Квадрат отклонения с учетом частоты	Куб отклонения с учетом частоты	Четвертая степень отклонения с учетом частоты
			-10,53	- 31,59	332,6427	(8-18,53)33	(8-18,53)43
			-6,53	-52,24	341,127	- - -	- - -
			- 2,53	-40,48	102,4144	- - -	- - -
			1,47	17,64	25,9308	- - -	- - -
			5,47	32,82	179,5254	- - -	- - -
			9,47	28,41	269,0427	(28-18,53)33	(28-18,53)43
			13,47	26,94	362,8818	- - -	- - -

По данным колонок 6, 7, 8 рассчитывают соответственно дисперсию (𝔖²), асимметрию (As) и эксцесс (E) по формулам, приведенным в разделе.

В такой же последовательности строят ВР по высоте.

Таблица 2.

Вариационный ряд по высоте.

№	Классовый интервал	Срединное значение интервала yi	Частота
	7,5 - 10,5		4
	10,6 – 13,5		4
	13,6 - 16,5		6
	16,6 – 19,5		15
	19,6 – 22,5		15
	22,6 – 25,5		5
	25,6 – 28,5		1

2.4. Ошибки выборочных характеристик и оценка параметров генеральной совокупности.

Рассчитанные в предыдущем разделе характеристики выборочной совокупности называются точечными. Это название используется для разделения оценок выборочной и генеральной совокупностей. Точечная оценка (характеристика) выборки (, 𝔖, V) в пределах самой выборки исчерпывающее ее описывает. Однако, сами характеристики выборки существенно зависят от ее объема: для выборок разного объема перечисленные характеристики будут иметь разные значения. Поэтому для характеристики параметров генеральной совокупности применяются интервальные оценки.

Для интервальной оценки параметров генеральной совокупности необходим предварительный расчет ошибок характеристик выборочной совокупности. Эти ошибки называются ошибками выборочности, чем подчеркивается зависимость их величин от размера выборки. Зависимость – обратная: чем больше объем выборки, тем меньше ее ошибка относительно величины аналогичного генерального параметра.

Для средней арифметической выборки ошибка выборочности равна:

(14)

где: 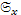– среднеквадратическое отклонение выборки, составленной из

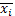(i от 1 до N), но берется 𝔖 из исследуемой выборки, N – объем этой выборки.

Выборочная ошибка среднеквадратического отклонения, т.е. оценка аналогичного параметра генеральной совокупности рассчитывается по формуле:

(15)

Ошибка коэффициента вариации

Ошибка асимметрии

Ошибка коэффициента эксцесс

Перечисленные ошибки зависят от объема совокупности, по которой они рассчитываются. Отсюда следует, что они обладают вероятностной природой. Значит, говорить о точности статистических оценок можно только с учетом вероятности распределения частот на графике-полигоне (гистограмме), строго говоря, на графике плотности распределения вероятности.

Нормированная кривая распределения приведена на рисунке 5. Ось абсцисс представлена собственно тремя осями: первая – ось значений признака, вторая – ось значений признака, пересчитанных в 𝔖 - мах, третья – ось значений признака, пересчитанная в долях нормированных отклонениях.

--граффик.

Ось Х соответствует значениям таблицы ВР. Особенностью нормального распределения является закономерность распределения частостей по диапазонам 𝔖 или t. Для нормального распределения всегда в диапазоне –𝔖 - +𝔖 лежит 68,3% вариант общего объёма значений признака, от –2𝔖 до 2𝔖- 95,5%, от -3𝔖 до 3𝔖 - 99,7% всех вариант совокупности.

Таким образом, единицу нормированного отклонения 𝔖, так же как и t, можно свзять с вероятностью значений признака. Это следует также из формулы нормированного отклонения, записанной в таком виде:

(19)

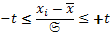
После преобразования получим:

(20)

Это и есть доверительный интервал, в котором будет находится значение средней величины любой выборки с вероятностью, определяемой величиной t. При t=1,00 мы будем иметь 68% вероятность, при t=1,96(2,0) – вероятность равна 95,5%, при t=3 диапазон возможных значений средней величины перекрывает 99,7% всех возможных значений. Это неравенство справедливо и в том случае, если речь идет о генеральной средней µ.

Приведенные формулы касаются только одного параметра – среднего значения. Но вся логика оценки не меняется относительно других параметров генеральной совокупности, кроме, пожалуй, асимметрии и эксцесса.

Дело в том, что значение генерального параметра для этих показателей известно – они равны нулю. Тогда формула этих показателей принимает несколько иной вид:

(21)

(22)

Полученное значение t сравнивают с табличным (приложение №2). Если оно меньше табличного, нет оснований считать, что полученное значение коэффициента существенно отличается от генерального параметра. Наоборот, если t > табличного значения, значит различие рассчитанного на выборке параметра существенно отличается от параметра генеральной совокупности, а следовательно обусловлено неслучайными воздействиями.

Результаты оценки параметров в генеральной совокупности нужно свести в таблицу вида:

Таблица 15.

Интервальная оценка параметров генеральной совокупности.

Характеристика выборки	Ошибка характеристики выборки	Интервальная оценка параметра	Показатель точности оценки
𝔖
V
As
E

Полученные результаты по интервальной оценке необходимо сопроводить соответствующими комментариями.

Используемый в таблице 15 показатель точности рассчитывается по формуле

По величине этого показателя судят о степени отклонения выборочной характеристики от генерального параметра. Показатель точности считается приемлемым, если он лежит в пределах 5%.

4. Оценка соответствия эмпирического распределения теоретическому.

Оценка полученных рядов распределения по диаметру и по высоте с точки зрения их соответствия теоретическому распределению производится по так называемым критериям согласия. В контрольной работе используются два из них: критерий Колмогорова λ(лямбда) и критерий Пирсона (хи-квадрат).

Первый критерий относительно прост, не требует использования характеристик выборочной совокупности и поэтому называется непараметрическим.

Расчет теоретических частот нормального распределения

Таблица 16.

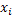
№	Классовая варианта	Частота	Нормированное отклонение	ƒ(ί) (Табличн.) т.3 прил.	Теорет. частота ƒ(ί)
					50*4

(1)

В формуле: k – величина интервала.

ƒ(ί) – из колонки 5.

Критерий λ рассчитывается по формуле:

(23)

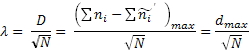
где: D – максимальная разность между эмперическими и теоретическими накопленными частотами в ВР.

Таблица 17.

Расчет критерия λ.

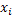
№	Классовая варианта.	Частоты.	Накопленные частоты.	Разница.
эмп.	теор.	эмп.	теор.

В шестой колонке находят класс, в котором разница между накопленными частотами максимальна. Подставляют его в формулу 23 и получают соответствующее значение λ.

Разница между накопленными эмпирическими и теоретическими частотами оцениваются по трем уровням доверительной вероятности: = 0,95, = 0,99, = 0,999. Этим уровням соответствуют значения λ: 1,36;. 1,63; 1,95.

Расхождение частот признаются случайными, а следовательно, соответствующим теоретической частоте, если значение λ не превосходит своего критического значения при принятом уровне доверительной вероятности (таблица №4 приложений).

Критерий χ ² аналогичен по структуре формуле дисперсии. То есть χ ² – это относительная сумма квадратов отклонений эмпирических частот от теоретических:

(24)

где: – эмпирическая частота.

– теоретическая частота. (см. таблицу 17)

Смысл оценки состоит в том, что чем в меньшей степени эмпирические частоты отклоняются от теоретических, тем с большей вероятностью можно говорить о степени соответствия эмпирического распределения теоретическому.

Таблица 18.

Date: 2015-10-19; view: 850; Нарушение авторских прав