Определение постоянной Ридберга

Атом водорода является простейшим атомом, состоящим из протона, в кулоновском поле которого движется один электрон. Естественно поэтому, первые исследования, связанные с построением атомной модели, были посвящены атому водорода, и, в частности, изучению его спектров.

Еще в XIX веке было замечено, что спектр водорода можно представить в виде нескольких серий, лежащих в разных спектральных областях, но, тем не менее, имеющих сходную структуру (рис.1).

Каждая оптическая серия состоит из ряда линий, расстояние между которыми по мере продвижения в сторону коротких волн уменьшается и заканчивается границей, соответствующей линии с минимальной длиной волны. Яркость линий одной серии уменьшается при уменьшении длины волны. Вышеперечисленные свойства характерны для всех серий.

Швейцарский ученый Иоганн Бальмер изучил серию, четыре линии которой лежат в видимой части спектра (а остальные - в ультрафиолетовой). Эмпирически он нашёл формулу, позволявшую подсчитать длину волны любой линии этой серии, путём подстановки в неё целых чисел:

(1)

где n = 3, 4, 5,...

Эта серия получила название серии Бальмера.

Последняя формула была несколько видоизменена шведским спектроскопистом Иоганнесом Ридбергом, записавшим её через волновые числа =1/λ

, (2)

где R=4/В - постоянная Ридберга.

Оказалось, что все остальные серии могут быть описаны аналогич­ными формулами, отличающимися величинами первого члена в скобках:

, (3)

где: т =1,2,3,4,5 определяют название серии (т= 1 – серия Лаймана, т =2 - серия Бальмера, т =3 – серия Пашена, т =4 – серия Бреккета, т =5 – серия Пфунда), п = т+1, т+2.

Ритц ввёл в рассмотрение понятие спектрального терма Т (т) ~R/m² и сформулировал принцип, названный его именем, согласно которому волновое число любой спектральной линии водорода можно представить как комбинацию некоторых двух термов

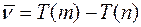(4)

Датский физик Нильс Бор, анализируя спектры различных атомов, сформулировал постулаты, согласно которым: 1) атомы могут находиться лишь в определенных (дискретных) энергетических состояниях, в которых они не поглощают и не излучают энергию, и 2) излучение и поглощение света атомом может происходить лишь скачком при переходе из одного состояния в другое, при этом излучается (или поглощается) квант света с энергией Е=hν, причем

hν = E_n - E_m ,(5)

где E_n, E_m - некоторые дискретные значения энергии атома.

В комбинационном принципе Ритца Н.Бор увидел прямое указание на соответствие между спектральными термами и стационарными состояниями атомов. В самом деле, формулу (5) можно преобразовать следующим образом:

= =

или

= - (6)

Отсюда легко получить формулу для энергии водородного атома, используя выражения для спектральных термов.

Сравнивая (6) с (4), получим:

, ,

откуда

(7)

Формула (7) позволяет вычислить энергию любого энергетического состояния водорода по известным значениям R, h, с и номеру уровня п. Всю совокупность изложенных данных удобно проиллюстрировать с помощью энергетической диаграммы, получившей название диаграммы Гротриана (рис. 2). Стрелками указаны переходы, соответствующие воз­никновению различных серий водородного атома.

Е, эВ

Рис. 2. Диаграмма Гротриана.

В настоящей работе мы определяем с помощью спектрального аппарата (гониометра) длины волн трёх линий серии Бальмера, лежащих в видимой части спектра. Эти три линии – красная, зеленая и фиолетовая возникают благодаря переходам электрона из состояния с n = 3, 4, 5 на уровень с п = 2. Определив длины волн этих линий, можно вычислить постоянную Ридберга, воспользовавшись формулой (8):

, (8)

где: п = 2, а ℓ = 3, 4, 5,…

Date: 2015-10-19; view: 711; Нарушение авторских прав