Проверка гипотезы о принадлежности двух выборок к одной и той же генеральной совокупности

Пусть имеются две серии независимых испытаний однородных величин х и у. При этом наблюденные значения х_i и у_i дают различные значения средних (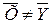 или обнаруживают различные рассеивания (). Возникает вопрос, можно ли считать эти расхождения существенными или они носят случайный характер. Например, с двух станков, настроенных на обработку одних и тех же деталей, взяты две текущие выборки. Средние и дисперсии этих выборок отличаются друг от друга. При этом закон распределения генеральных совокупностей, из которых взяты выборки, неизвестен. Требуется проверить, обеспечивают ли оба станка одинаковую точность обработки.

Нулевая гипотеза в данном случае будет заключаться в том, что функции распределения х и у тождественны, т. е. выборки принадлежат одной и той же генеральной совокупности. Для проверки этой нулевой гипотезы может быть использован критерий Вилькоксона, основанный на числе инверсий. Под инверсиями в данном случае понимается следующее. Наблюденные значения х и у в двух выборках располагают в общую последовательность в порядке возрастания, например, в виде

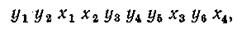
где — члены первой выборки, а - члены второй выборки.

Если какому-либо значению х предшествует некоторый у, то говорят, что эта пара дает инверсию. Если некоторому значению х_m предшествует n значений у, то это значит, что х_m имеет n инверсий. Например, в нашей последовательности х₁ дает две инверсии, х₂ — то же две инверсии, х ₃ — пять инверсий и x ₄ — шесть инверсий. Всего инверсий в нашей последовательности будет

Нулевая гипотеза принимается, если число u будет лежать внутри некоторых предельных или критических значений, вычисляемых для принятого уровня доверительной вероятности. Расчет критических значений для u производится из следующих соображений. Если объемы выборок n > 10 и m > 10, то число инверсий u распределяется приблизительно по нормальному закону со средним значением (математическим ожиданием)

и дисперсией

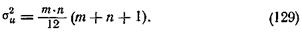
Поэтому предельные значения u определяются границами

где t зависит от принятого уровня доверительной вероятности q и вычисляется по таблице значений Ф (t) (см. приложение 1) по формуле

откуда

Например для q — 0,05

Этому значению Ф (t) по таблице приложения 1 соответствует t = 1,96.

Таким образом, если наблюденное значение u будет лежать внутри границ, определяемых неравенством (130), или не выходить за пределы критических областей:

то нулевая гипотеза принимается, в противном случае она отвергается. Так как u имеет приближенно нормальное распределение только при выборках объема u > 10 и m > 10, то для использования критерия Вилькоксона необходимо брать выборки объемом не менее 12.

Контрольные вопросы:

1. В чем заключается статистическая проверка гипотез и какую роль она играет в исследованиях?

2. Какие критерии используются для проверки гипотезы о законе распределения случайной величины?

3. Какие способы применяются для проверки гипотезы случайности выборки?

4. Какие критерии используются для проверки гипотезы равенства двух выборочных средних и дисперсий?

5. Какие критерии используются для проверки гипотезы о принадлежности двух выборок к одной и той же генеральной совокупности?

Лекция №6. Корреляционные связи [1, с. 253…280; 5, с. 590…660; 9, с. 93…112]

6.1. Понятие о стохастических и корреляционных связях

6.2. Коэффициент корреляции и корреляционное отношение

6.3. Прямолинейная корреляционная связь

6.4. Криволинейная корреляционная связь

6.5. Понятие о множественной корреляции

6.6. Корреляционный и регрессионный анализ