Проверка гипотезы о законе распределения случайной величины

Для установления закона распределения генеральной совокупности по большой выборке из нее пользуются рядом критериев, из которых наибольшее практическое применение имеют критерий l А.Н. Колмогорова и критерий c² Пирсона.

Критерий l дает достаточно точные результаты даже при объеме выборок, состоящих из нескольких десятков членов и прост для вычислений. Не вдаваясь в теоретические обоснования этого критерия, приведем лишь порядок его использования.

Для вычисления величины l необходимо предварительно определить эмпирические F_n (x) и теоретические F (х) функции предполагаемого закона распределения для каждого наблюденного значения случайной величины х. Затем по максимальной разности этих функций определяется l при помощи следующей формулы:

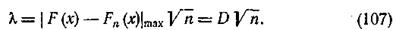
Так как - накопленные теоретические и эмпирические частоты, а n — объем выборки, то вместо формулы (107) можно пользоваться также следующей формулой:

Накопленной частотой любого m -го значения x_i называется сумма частот всех предшествующих значений x_i включая и частоту самого x_i т.

е.

По вычисленному значению l по формуле (107) или (108) и приложению 12 определяют Р (l). Если вероятность Р (l) окажется очень малой, практически, когда Р (l) £ 0,05, то расхождение между F (х) и F_n (x) считается существенным, а не случайным и гипотеза о предполагаемом законе распределения величины х бракуется. Если же вероятность Р (l) будет достаточно большой (практически, когда Р (l) > 0,05), то гипотеза принимается.

Необходимо заметить, что использование критерия l предполагает непрерывность F (х) и, кроме того, предполагается, что эмпирическая функция F_n (x) построена по не сгруппированным интервалы значениям случайной величины х. Однако, когда интервалы группировки достаточно малы, критерий l дает, хотя и приближенную, но вполне приемлемую для практических целей оценку близости эмпирического распределения к теоретическому.

Критерий c² применим для любых сгруппированных совокупностей, но при достаточно большом их объеме. Для вычисления c² необходимо предварительно вычислить теоретические частоты для наблюденных значений эмпирического распределения, т. е. произвести сопоставление этого распределения с предполагаемым теоретическим. При этом необходимо, чтобы частоты интервалов значений х были бы не менее пяти. Если в каком-либо интервале значений х частота будет менее пяти, то такой интервал следует. Объединить с соседним.

Критерий c² вычисляется по следующей формуле:

Если Р (c²) £0,05, то наша гипотеза о законе распределения должна быть забракована. Если Р (c²) > 0,05, то гипотеза принимается.

Date: 2015-10-19; view: 409; Нарушение авторских прав