Линеаризация

Для того, чтобы оценить неизвестные параметры β₀ , …, β_n нелинейной регрессионной модели, необходимо привести ее к линейному виду. Суть линеаризации нелинейных по независимым переменным регрессионных моделей заключается в замене нелинейных факторных переменных на линейные. В общем случае полиномиальной регрессии процесс замены нелинейных переменных функции п-го порядка выглядит следующим образом: x = с₁,; х² = c₂; x^З = с₃;...; x^п = c_п.

Тогда уравнение множественной нелинейной регрессии можно записать в виде линейного множественного регрессионного уравнения

y_i = β₀ + β₁x_i + β₂x²_i + … +β_nxⁿ_i + ε_i =>

=> y_i = β₀ + β₁c_1i + β₂c_2i + … +β_nc_ni + ε_i

Гиперболическую функцию также можно привести к линейному виду с помощью замены нелинейной факторной переменной на линейную. Пусть 1/ х = с. Тогда исходное уравнение гиперболической функции можно записать в преобразованном виде:

y_i = β₀ + β₁ / x_i + ε_i => y_i = β₀ + β₁с_i + ε_i

Таким образом, и полиномиальную функцию любой степени, и гиперболоид можно свести к модели линейной регрессии, что позволяет применять к преобразованной модели традиционные методы нахождения неизвестных параметров уравнения регрессии (например, классический МНК) и стандартные методы проверки различных гипотез.

Ко второму классу нелинейных моделей относятся регрессионные модели, в которых результативная переменная y_i нелинейно связана с параметрами уравнения β₀ ,…, β_n. К такому типу регрессионных моделей относятся:

1) степенная функция

y_i = β₀ · x _i ^β1 · ε_i

2) показательная функция

y_i = β₀ · β₁^xi · ε_i

3) логарифмическая парабола

y_i = β₀ · β₁^xi · β₂^xi · ε_i²

4) экспоненциальная функция

y_i = e ^β0+β1xi · ε_i

5) обратная функция

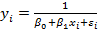
и другие.

Нелинейные по параметрам регрессионные модели в свою очередь делятся на модели подлежащие линеаризации (внутренне линейные функции) и неподлежащие линеаризации (внутренне нелинейные функции). Примером моделей, которые можно свести к линейной форме, является показательная функция вида y_i = β₀ · β₁^xi · ε_i, где случайная ошибка ε_i мультипликативно связана с факторным признаком x_i. Д анная модель нелинейна по параметру β₁. Для ее линеаризации вначале осуществим процесс логарифмирования:

ln y_i = ln β₀ + x_i ·ln β₁ + ln ε_i

Затем воспользуемся методом замен. Пусть ln y_i = Y_i; ln β₀ = А; ln β₁ = В; ln ε_i = Е_i.

Тогда преобразованная показательная функция имеет следующий вид:

Y_i = А + В x_i + Е_i.

Следовательно, показательная функция y_i = β₀ · β₁^xi · ε_i является внутренне линейной, и оценки ее параметров могут быть найдены с помощью традиционного метода наименьших квадратов.

Если же взять показательную функцию, включающую случайную ошибку ε_i аддитивно, т.е. y_i = β₀ · β₁^xi+ ε_i, то данную модель уже невозможно привести к линейному виду с помощью логарифмирования. Она является внутренне нелинейной.

Пусть задана степенная функция вида y_i = β₀ · x _i ^β1 · ε_i. Прологарифмируем обе части уравнения:

ln y_i = ln β₀ + β₁·ln x_i + ln ε_i

Теперь воспользуемся методом замен: ln y_i = Y_i; ln β₀ = А; ln x_i = X_i; ln ε_i = Е_i.

Тогда преобразованная степенная функция имеет следующий вид:

Y_i = А + β₁ X_i + Е_i.

Степенная функция также является внутренне линейной и ее оценки можно найти с помощью традиционного метода наименьших квадратов. Но если взять степенную функцию; виде уравнения y_i = β₀ · x _i ^β1+ ε_i, где случайная ошибка аддитивно связана с факторной переменной, то модель становится внутренне нелинейной.

Date: 2015-10-19; view: 1085; Нарушение авторских прав