Частные уравнения, частная корреляция

Уравнение множественной линейной регрессии характеризует весь исследуемый процесс в целом. На его основе могут быть построены частные уравнения регрессии, которые связывают результативный признак с соответствующим фактором х_i при закреплении других, учитываемых в уравнении множественной регрессии на среднем уровне:

y_{x1 x2,x3,...,xp} = a +b₁x₁ + b₂x₂ + b₃x₃+ … + b_px_p

y_{x2 x1,x3,...,xp} = a +b₁x₁ + b₂x₂ + b₃x₃+ … + b_px_p

……………………………………………………

y_{xp x1,x2,...,xp-1} = a +b₁x₁ + b₂x₂ + b₃x₃+ … + b_px_p

Частные уравнения регрессии характеризуют влияние только определенного фактора на результат, так как другие закреплены на неизменном среднем уровне. На основе частных уравнений регрессии можно найти частные коэффициенты эластичности. Они показывают, на сколько процентов в среднем изменится результат при изменении соответствующего фактора на 1% при постоянных значениях всех остальных факторов. Эти коэффициенты рассчитываются по следующей формуле:

rде b_i - коэффициент «чистой» регрессии для фактора x_i в уравнении множественной регрессии; y_{xi x1,x2,…,xi-1,xi+1,...,xp} - частное уравнение регрессии для фактора x_i, для множественной линейной регрессии оно принимает следующий вид:

a +b₁x₁ + b₂x₂ + … +b_i-1x_i-1+ b_ix_i + b_i+1x_i+1…+ … + b_px_p

Частные коэффициенты эластичности рассчитываются для каждого наблюдения и характеризуют влияние фактора именно на его результат. Кроме того, могут быть найдены и средние коэффициенты эластичности, которые будут характеризовать влияние каждого фактора на результат в среднем по совокупности:

где x_i - среднее арифметическое по ряду наблюдений фактора x_i; y_{xi,x1,x2,…,xi-1,xi+1,...,xp} - среднее по частному уравнению регрессии для фактора x_i во множественной линейной регрессии оно принимает вид:

a +b₁x₁ + b₂x₂ + … + b_px_p

Коэффициенты эластичности можно использовать при отборе факторов для множественной регрессии. В данном случае сравниваются либо средние по совокупности коэффициенты эластичности, либо коэффициенты эластичности для конкретного наблюдения, если надо установить силу влияния каждого фактора при этом наблюдении.

Во множественном регрессионном анализе возникает проблема определения тесноты связи между двумя признаками в «чистом» виде, т.е. при устранении воздействия других факторов. Это можно сделать только для учтенных в модели факторов. Показателем «чистого» влияния фактора на результат является частный коэффициент корреляции.

Рассмотрим пример двухфакторной модели у_х = a + b₁x₁ + b₂x₂. Коэффициенты частной корреляции, показывающие в «чистом» виде тесноту связи фактора и результата, для двухфакторной модели рассчитываются через коэффициенты детерминации по следующим формулам:

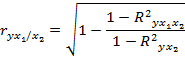
Эти коэффициенты являются частными коэффициентами корреляции первого порядка, так как они фиксируют тecноту связи фактора и результата при постоянном воздействии одного фактора.

Для расчета коэффициентов частной корреляции могут быть использованы парные коэффициенты корреляции. Для двухфакторной модели коэффициенты частной корреляции первого порядка вычисляются следующим образом:

При дополнительном включении в модель фактора x_i частный коэффициент корреляции рассчитывается по формуле:

где R²_{yx1x2…xi...xp}, R²_{yx1x2…xi-1 xi+1…xp} – множественный коэффициент детерминации для модели множественной регрессии соответственно со всем количеством факторов и с р-1, где в модель не введен фактор x_i.

Значения частных коэффициентов корреляции, рассчитанные таким способом, изменяются от нуля до единицы. Соответственно, чем ближе частный коэффициент корреляции к единице, тем теснее связь между определенным фактором x_i и результатом у при неизменном уровне всех других факторов, включенных в уравнение регрессии. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается: (р-1).

Коэффициенты частной корреляции более высоких порядков так же, как и для двухфакторной модели, можно рассчитывать, используя частные коэффициенты корреляции более низких порядков:

Такие формулы расчета коэффициентов частной корреляции называются рекуррентными, коэффициенты частной корреляции, рассчитанные по ним, изменяют свое значение от -1 до 1. Чем ближе по модулю коэффициент частной корреляции к единице, тем теснее связь фактора и результата при устранении влияния прочих факторов, включенных в модель.

Частные коэффициенты корреляции используются не только для ранжирования факторов по степени влияния на результат, но и для их отбора. При низких значениях коэффициентов нет смысла вводить в модель дополнительные факторы и тем самым лишь усложнять ее.

Date: 2015-10-19; view: 513; Нарушение авторских прав