Принцип взаимности отношений между элементами геометрических систем

Известно, что одним из важнейших принципов образования объектов концепту-ального пространства является большой принцип двойственности, сущность которо-го состоит в замене слов «точка» и «плос-кость» друг на друга в различных рассужде-ниях, а также малый принцип двойственно-сти для компланарных элементов, когда ме-няются местами слова «точка» и «прямая».

Наиболее наглядно большой принцип двойственности проявляется в особеннос-тях геометрических структур таких правиль-

ных многогранников, как гексоэдр и октаэдр, додекаэдр и икосаэдр, которые, в связи с этим, называются взаимными. Природа их взаимности, очевидно, объясняется не толь-ко тем, что все двойственные фигуры взаи-мны, но также и тем, что эти фигуры, как та-ковые, являются системами взаимно свя-занных конкретных вершин, ребер и граней. конкретными отношениями принадлежнос-ти и пересекаемости, также обладающие свойством взаимности.

Очевидно, что принцип двойственности раскрывает особенности «объектного» на-полнения концептуального пространства, однако на процесс мысленного эксперимен-тирования с этими объектами для синте-зирования из них концептуальных моделей объектов-систем оказывает большее влия-ние не столько этот принцип, сколько конструктивные особенности используемых при этом взаимных связей и отношений между их элементами.

Практически это экспериментирование

сводится к решению позиционных задач на

установление отношений принадлежности

и пересекаемости между различными эле-ментами эвклидова пространства в различ-ных сочетаниях (рис.5.86)

Рассматривая конструктивные особен-ности отношения взаимной пересекаемос-ти, видим, что оно содержит в себе отноше-ние принадлежности, обладает его свойст-вами, а поэтому конструктивно может быть сведено к нему. Для примера сравним два пути конструирования трехэлементной сис-темы «точка, прямая, плоскость»: по перво-му пути необходимо решить позиционную задачи на определение точки пересечения данной прямой с данной плоскостью, по второму для получения той же системы через данную точку следует провести преж-де прямую, а затем плоскость, подчинив их положение в пространстве наперед задан-ным условиям. Второй путь представляется более простым и более практичным.

Реальные искусственные объекты, соз-данию которых предшествует их проектиро-вание, многоэлементны. Они имеют иерар-хическое строение и включают в себя двух,- трёх- и более элементные системы как свои подсистемы, которые взаимно связываются в проектируемую систему.

Понимание проектируемого объекта как многоэлементной системы требует оптими-зации представления его структуры. Такая оптимизация становится возможной на ос-нове использования фундаментального от-ношения взаимной принадлежности с использованием, в случае необходимости, принципа двойственности. В результате предлагается следующая концептуальная технология образования двух-, трёх- и бо-лее элементных систем, состоящих из то-чек А, В, С,…, прямых линий а, b, c,…и пло-скостей a, b, g, обозначаемых в соответ-ствии с их точечностью соответственно

цифрами 1, 2 и 3 (рис.5.87)

ОБРАЗОВАНИЕ ГЕОМЕТРИЧЕСКИХ СИСТЕМ ТОЧЕК, ПРЯМЫХ И ПЛОСКОСТЕЙ НА ОСНОВЕ ОТНОШЕНИЯ ВЗАИМНОЙ ПРИНАДЛЕЖНОСТИ Си-сте-мы № п/п   Элементы Исходные системы   Элемены Взаимные системы   Эскиз Наиме- нование   Эскиз Наиме-нование   2-х - э л е м е н т н ы е     1. 1.2 А Î а   Точка на прямой 2.1 a É A   Две полу- прямые, луч     2. 1.3   А Î a   Точка в плоскости 3.1   a É A Плоскость, проходя-щая через точку     3. 2.3 а Î a   Прямая в плоскости 3.2   a É a   Две полу-плоскости   3-х- э л е м е н т н ы е     4. 1, 1.2   А,В Î а   Отрезок АВ прямой а 2,2.1 a, b É A a ⊥ b É A Линейный угол, прямой угол     5. 1, 1.3   А,В Î a   Две точки в плоскости 3,3.1 a, b Î A   Двугран-ный угол   6. 2, 2.3 а,b Î a   Комплана-рные прямые 3,3.2   a, b É a   Двугран-ный угол   4-х- э л е м е н Т н н е   7.   1.1,1.2   А,В,С Î а   Три коллиней-ные точки 2.2, 2.1   a, b, c Î A 3-лучевая связка, оси координат   8.   1.1,1.3   А, В, С ….Îa Три компланар-ные точки 3.3,3.1   a,b,g É A 3-гранный угол, коор-динатные плоскости   9.   2.2,2.3 а,b,с Î a Три комп-ланарнные прямые 3.3,3.2   a,b,g É a   Пучок 3-х плоскостей   М   н   о   г   о   э   л   е   м   е   н   т   н   ы   е     ¥ 1,3 А,В,С, …Î а   Точечный ряд ¥ 2.1 a,b,c,…É É A Пучок прямых, связка прямых     ¥ 1.3 А,В,С, …Îa   Плоское поле точек ¥ 3.1 a,b,g, …É É A   Связка плоскостей     ¥ 2.3   а,b,с,…Î a   Плоское поле прямых ¥ 3,2 a,b,g É a   Пучок плоскостей     ¥ 2,1¥ а,в,с,... Î А ¥ Связка па- раллельных прямых ¥1¥, A,B,C,… É a¥ Несобст- венный точечный ряд     ¥ 3,2¥ a, b, g, … Î А ¥ Связка кон-курентных плоскостей ¥1¥,3 A¥,B¥,C¥ Î a   Несобст-венная прямая плоскости       ¥ 3,3¥ a, b, g … Î а ¥   Связка па-раллельных плоскостей ¥2¥,3 a¥b¥,c¥… Î a¥   Несобст-венное поле прямых       ¥ 2,¥ 1Î2 (а,b,…) É É (A.B, … Î n)   Линейный комплекс ¥ 1,¥ 2 É 1 A, B, …É (а,b,…) Î Î a   Связка точечных рядов       ¥2, ¥ 1 Î3 a,b,…É É(A,B,…) Î a 2-парамет-рическое множество связок прямых ¥ 1,¥ 2Î1 A,B,… É É(a,b,…)Î Î a Плоское поле точечных рядов

Здесь формообразующим фак-тором преобразования исходной си-стемы во взаимную принято сочета-ние принципов двойственности и взаимности, когда с заменой эле-ментов исходной системы на им двой-ственные заменяются слова «пересе-каются» («касаются») на слова «про-ходит через».

Если дополнительно к точкам 1, прямым 2 и плоскостям 3 в качестве элементов принять кривые линии 2¢ и

кривые поверхности 3¢, то диапазон возможностей формообраования как исходных, так и взаимных им геомет-

рических систем по приведенной тех-нологии резко расширяется и охваты-вает, по сути дела, все те варианты их структур, которые входят в проек-тируемые объекты как их подсистем-мы.

Нетрудно видеть, что совместное использование принципа двойствен-ности элементов различных систем и принципа взаимности отношения при-надлежности между этими элемен-тами возможно при наличии хорошо развитого пространственного вообра-жения и способствует развитию конструктивно-композиционного мыш-ления как обязательной профессио-нальной способности любого созда-теля искусственных материльных систем.

Выводы:

1. Системный анализ конструк-тиных свойств различных взаимных отношений между элементами гео-метрических систем показывает,

что фундаментальным является отношение принадлежности, а ос-новным формообразующим принци-пом создания новых систем явля-ется принцип взаимности этих от-ношений

2. Предлагаемая технология образования геометрических систем на основе отношения взаимной при-надлежности между их элементами, с одной стороны, раскрывает сис-темную природу известных объек-тов, а с другой стороны, позволяет достаточно просто конструиро-вать им взаимные объекты, но иной структуры, что представляет как теоретический, так и практический интерес.

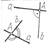
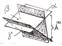
Рис. 5.87. Таблица образования систем, взаимных данным

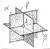
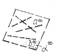
Рис.88. Известные точки, линии и

фигуры в структуре остроугольного треугольника

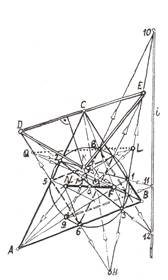
Рис.5.89. Новые точка Х, линии и фигуры в структуре остроугольного треугольника

Все вышеперечисленные понятия о взаимных связях и отношениях между эле-ментами эвклидова пространства, а также о простейших геометрических системах, рас-крывающие конструктивные особенности их структур, легко представляемы мысленно, что даёт сознанию возможность свободного концептуирования и возбуждает развитие профессионального мышления вплоть до креативного.

Ярким примером этому является синте-тическое исследование структуры произво-льного остроугольного треугольника, содер-жащей как известные замечательные точки и линии, так и новые, подлежащие изуче-нию.

Разносторонний остроугольный треугольник является наиболее изученной геометрической фигурой. Однако, если его представить как гра-фическую систему трёх конкурентных и компла-нарных отрезков-сторон, то оказывается, что, не смотря на её «произвольность», часть ограни-ченного ею картинного пространства имеет стро-го закономерную и не до конца изученную струк-туру.

К числу хорошо изученных элементов этой структуры и связей между ними относятся её за-мечательные линии, точки и фигуры: высоты,- медианы,медиатрисы, биссектрисы, орто-центр F, центр тяжести М и центр описанно й окружности N, расположенные на прямой Эйле - ра,окружность Фейербаха или окружности 9точек, а также срединный 456 и ортотреуголь - ник 123 (рис.5.83).

К числу замечательных свойств этих элемен-тов относятся:

- инвариантность прямой Эйлера, которая точкой М делится в отношении 1: 2 и, тем самым, собою кодирует породивший её треугольник;

- равноудалённость середины о прямой Эй-лера от середин сторон треугольника АВС и ос-нований его высот, что делает его центром окру-жности Фейербаха, пересекающей высоты дан-ного треугольника АВС в серединах7,8,9 рас-стояний от его вершин до ортоцентра F;

конгруэнтности срединного треугольника 456 треугольникам А56, В46 и С45 и его подобие треугольнику АВС;

«высотность» медиатрис треугольника АВС в срединном треугольнике 456;

- «биссектрисность» высот треугольника АВС в ортотрегольнике 123.

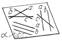
Рассматривая особенности позиционного расположения перечисленных элементов, заме-чаем (рис.5.89), что:

1. Точки 7,8,9 пересечения окружности Фейербаха с высотами треугольника АВС в сере-динах расстояний его вершин до ортоцентра яв-ляется вершинами треугольника 789, подобного данному и конгруэнтного срединному, но по-вёрнутому относительно него на 180° и поэтому названного антисрединным [110]

2. Точки D, E, K пересечения продолжения

сторон срединного и ортотреугольника, вершины которых лежат на смежных сторонах данного треугольника, являются вершинами ортосредин -

ного треугольника DEK, стороны которого при

продолжении проходят через вершины А, В, С данного треугольника;

3. Высота, опущенная из вершины К орто-срединного треугольника на его сторону DE, при продолжении проходит через центр о окружно-сти Фейербаха;

4. Точки L, Q, H пересечения сторон сре-динного и ортотреугольника, вершины которых лежат на несмежных сторонах данного треуго-льника, инцидентны прямым LA, QB, HC,, прохо-дящим через вершины данного треугольника и соответственные вершины фигуры наложения срединного и ортотреугольника и пересекающих-ся в некоторой точке Х, природа которой требует изучения;

5. Точки 10, 11, 12 пересечения сторон анти-срединного треугольника, соответственных сто-ронам срединного, со сторонами ортотреуго-льника, располагаются на одной прямой і как оси гомологии между этими треугольниками при це-нтре гомологи в ортоцентре F треугольника АВС.

6. Точка Х, в которой пересекаются прямые, соединяющие вершины треугольников АВС и L QH, является центром гомологии этих треуго-льников, ось которой определяется точками пересечения их соответственных сторон, но в данном случае выходит за пределы рисунка.

Известно, что ось гомологии конструктивно является ребром двугранного угла, в гранях ко-торого лежат треугольники АВС и LQH, а тогда точка Х представляется вершиной некоторой пирамиды, основаниями верхней и нижней полы которой служат данные треугольники. Это озна-чает переход от планиметрической природы про-извольного треугольника к стереометрическому истолкованию конструктивных особенностей его структуры, что и является креативом, вызываю-щим познавательный интерес к абстрактным геометрическим построениям, дающим порой интересные практические результаты.

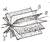
Примером может служить аналогичное син-тетическое исследование структуры равнобед-ренного треугльника профиля пирамиды фарао-на Хеопса (рис.5.90), в результате которого установлено, что:

Рис.5.90. Геометро-графическая структура поперечного профиля пирамиды фараона Хеопса

1. Треугольник профиля пирамиды состоит из двух прямоугольных треугольников Прейса, длины сторон которых составляют ряд золотого сечения;

2. «Камера царя» М расположена в центре

тяжести фигуры профиля;

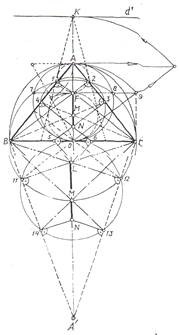
Рис.5.91. Система взаимосвязанных пирамид фараона Хеопса и Александра Холода.

3. «Камера царицы» N равноудалена от вер-

шин А, В, С профиля, т.е., является центром опи-санной вокруг него окружности;

4. Ортоцентр F профиля практически совпа-

дает с фокусом золотого эллипса, описанного вокруг него, так как этот фокус делит высоту профиля в золотом иотношении 0,382: 0,618;

5. Окружность Фейербаха пересекает ось симметрии профиля в «энергетическом центре» всей пирамиды, удалённой от её основания на величину, кратную числу 441,- значению частоты колебаний звука «ля», - мирового камертона [, c.14].

6. Направление основных туннелей, вентиля-ционных каналов и положение подземной каме-ры L определены простыми графическими по-строениями

Изотерическая мысль о том, что под надзем-ной пирамидой существует гипотетическая под-

земная энергетическая пирамида легко подтвер-- дилась точным графическим построением (рис. 5.82). Единственная точка надземного профиля,

расположенная под землёй (камера L), принятая

Date: 2015-10-18; view: 330; Нарушение авторских прав