Геометрический способ сложения сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил.

Величину, равную геометрической сумме сил данной системы, будем называть главным вектором этой системы сил.

Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, т.к. для многих систем сил, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 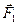, , …, (рис.2.3, a), откладываем от произвольной точки О (рис. 14, б) век­тор Oa, изображающий в выбранном масштабе cилу F ₁, от точки a откладываем вектор , изображающий силу F ₂, от точки b откла­дываем вектор bc, изображающий силу F ₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F_n. Соединяя начало первого вектора с концом последнего, получаем вектор = , изображающий геометрическую сумму или главный вектор слагаемых сил:

или

От порядка, в котором будут откладываться векторы сил, модуль и направление не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Рис.2.3

Фигура, построенная на рис.2.3, б, называется силовым (в общем случае векторным) многоугольником. Таким обра­зом, геометрическая сумма или главный вектор несколь­ких сил изображается замы­кающей стороной силового многоугольника, построенно­го из этих сил (правило сило­вого многоугольника). При построении векторного многоугольника следует помнить, что у всех слагаемых векторов стрелки должны быть направлены в одну сторону (по обводу многоугольника), а у вектора – в сторону противоположную.

Равнодействующая сходящихся сил. При изучении статики мы будем последовательно переходить от рассмотрения более простых систем сил к более сложным. Начнем с рассмотрения си­стемы сходящихся сил. Сходящимися называются силы, линии дей­ствия которых пересекаются в одной точке (рис.2.3, а).

По следствию из первых двух аксиом статики система сходящихся сил, действующих на абсолютно твердое тело, эквивалентна системе сил, приложенных в одной точке (на рис.2.3, а в точке А).

Последовательно применяя аксиому параллелограмма сил, прихо­дим к выводу, что система сходящихся сил имеет равнодей­ствующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке их пересечения. Следовательно, если силы 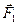, , …, сходятся в точке A (рис.2.3, а), то сила, равная главному вектору , найденному построением силового мно­гоугольника, и приложенная в точке А, будет равнодействующей этой системы сил.

Date: 2015-10-18; view: 497; Нарушение авторских прав