Частотное распределение и его параметры. Основные меры центральной тенденции и разброса

Распределением называется закономерность встречаемости признака и разных его значений. Статистическое распределение может иметь графическое представление в виде полигона частот (ломаной линии, соединяющей точки, соответствующие величинам частот, откладываемым по оси ординат). Форма распределения является некоторой обобщенной характеристикой выборки. Кривые распределения бывают одновершинные и многовершинные. В психологических исследованиях чаще всего ссылаются на нормальное распределение.

Нормальное распределение – вид распределения переменных, характеризуемое тем, что крайние значения признака в нем ссылаются достаточно редко, а значения, близкие к средней величине – достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественно-научных исследованиях и казалось “нормой” всякого массового проявления признаков. Это распределение следует закону, открытому в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции. График нормального распределения представляет симметричную унимодальную колоколообразную кривую (верхняя часть колокола), осью которой является вертикаль (ордината), проведенная через точку 0.

Рисунок 1. Процентное распределение случаев под нормальной кривой

Для любого нормального распределения в пределах М + 1s лежит около 68%, в пределах
М + 2s – 95%, М + 3s – 99,7% (М – среднее арифметическое).

Параметры распределения – это его числовые характеристики, указывающие, где в “среднем” располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. Характеристики совокупности переменных (признаков), указывающие на наиболее типичный, репрезентативный для изучаемой выборки результат называются мерами центральной тенденции. Наиболее практически важными мерами центральной тенденции являются математическое ожидание (или среднее арифметическое), мода, медиана.

а) Среднее арифметическое (М – оценка математического ожидания) – это обобщающий показатель положения уровня центра распределения. Оно вычисляется по формуле:

где хi – каждое наблюдаемое значение признака;

i – индекс, указывающий на порядковый номер данного значения признака;

n – количество наблюдений;

S – знак суммирования.

б) Медиана (Ме) – центральное значение переменной: результат, находящийся в середине последовательности показателей, если их расположить в порядке возрастания или убывания.

в) Мода (Мо) – наиболее часто встречающийся результат (самая высокая точка кривой распределения).

При выборе и интерпретации мер центральной тенденции необходимо учитывать следующие особенности и правила использования приведенных показателей.

1. При определении средних величин необходимо тщательное соблюдение требований однородности переменных, репрезентативности и достаточности объема выборки.

2. Расчету средних величин должна предшествовать предварительная разбивка изучаемой совокупности на качественно однородные группы.

3. Медиана не зависит от величин и частот встречаемости в рамках определенного множества переменных.

4. В малых совокупностях мода нестабильна и может сильно изменяться при единичных и незначительных вариациях переменных.

5. Каждое значение переменной влияет на величину средних. Если одно какое-нибудь значение меняется на С единиц, среднее арифметическое меняется в том же направлении на 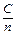единиц.

6. В унимодальных симметричных выборках среднее, медиана и мода совпадают.

7. Являясь обобщенной характеристикой ряда, меры центральной тенденции не позволяют учитывать его вариации. Наряду с мерами центральной тенденции обязательно использование мер изменчивости.

Различные меры изменчивости распределения характеризуют степень и характер вариации признаков.

Меры изменчивости – статистические показатели вариации (разброса) признака (переменной) относительно среднего значения, степени индивидуальных отклонений от центральной тенденции распределения. Меры изменчивости позволяют судить о достоверности и однородности полученной эмпирически совокупности данных, существенности сходств и различий в распределении и сравниваемых группах распределений, точности проведенных измерений. Среди прочих показателей к ним относятся: размах распределения, дисперсия, стандартное отклонение, показатели асимметрии и эксцесса.

Размах распределения – разность между самым высоким и самым низким результатом.

Дисперсия (S, s2) характеризует средний разброс значений по выборке относительно среднего арифметического, возведенный в квадрат. Расчет дисперсии применяют для выделения выборочной совокупности, определения ошибки выборки, однородности изучаемой совокупности по тому или иному признаку.

На практике, однако, чаще используют другой показатель – стандартное отклонение
(s или sх) – показатель, представляющий собой квадратный корень из несмещенной оценки дисперсии.

Дисперсия и стандартное отклонение (или среднее квадратичное отклонение) имеют некоторые недостатки. Они недостаточно точно характеризуют изменчивость признака, т.к. отражают абсолютный размер отклонений. Это неудобно при сопоставлении распределений с различной размерностью и значением признаков. Для устранения этого недостатка абсолютные числа переводятся в относительные. Отношение стандартного отклонения к средней, выраженное в процентах, называется коэффициентом вариации V:

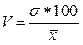
В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения. Показатель асимметрии (А) может быть положительным или отрицательным. При левосторонней, или положительной асимметрии в распределении чаще встречаются более низкие значения признака, а при правосторонней, или отрицательной – более высокие.

В тех случаях, когда какие-нибудь причины способствуют преимущественному появлению средних или близких к средним значений, образуется распределение с положительным эксцессом(Е).

Если же в распределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двухвершинное. В нормальных распределениях асимметрия равна нулю, эксцесс – трем.

Одним из коэффициентов, используемых в математической статистике, позволяющим определить достоверность различий параметров эмпирического распределения от теоретического (в т.ч. нормального) или ожидаемого является критерий c² . Критерий – определенная случайная величина, являющаяся функцией изучаемых случайных чисел и чисел степеней свободы. Критерий c² – характеристика распределения, используемая для проверки статистических гипотез. Он представляет собой сумму квадратов отклонений эмпирических частот (р) от теоретических или ожидаемых (р’), отнесенную к теоретическим частотам. Ограничение для применения данного критерия: минимальное значение эмпирической частоты не должно быть менее 10, а теоретической – менее 5 (если требование не выполняется, необходимо увеличить объем выборки или объединить интервалы группировки, суммируя их частоты).

Date: 2015-10-18; view: 3869; Нарушение авторских прав