
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Мореходная Астрономия, как учебная дисциплина. Построение пособия. 1 page
|
|
Дисциплина "Мореходная астрономия" имеет цель научить слушателей определять географические координаты места судна и поправку компаса по наблюдениям небесных светил, а также другие практические задачи, обусловленные движением светил.
Мореходная астрономия состоит из двух частей:
- сферической астрономии, без знания которой невозможно изучение астрономии;
- практической (мореходной) астрономии или астронавигации, обеспечивающей понимание и решение практических задач, необходимых судоводителю.
Дисциплина "Мореходная астрономия" имеет целью привить слушателям профессиональные навыки по их использованию для обеспечения безопасности мореплавания, включая подготовку приборов и инструментов в период подготовки к рейсу и во время плавания, а также решение задач по определению поправки хронометра, определение поправки компаса и места судна астрономическими способами.
Знания, умения и полученные в ходе изучения дисциплины навыки должны быть достаточны для того, чтобы решать перечисленные задачи во время ходовой вахты без дополнительной подготовки.
Программа предусматривает теоретическую часть обучения, лабораторные работы. Закрепление практических навыков предусматривается программой плавпрактики.
При составлении данного пособия были взяты за основу требования Международной конвенции по подготовке и дипломированию моряков и несению вахты 1978/95 г., Государственные требования к минимуму содержания и уровню подготовки выпускников по специальности 7.100 301 «Судовождение» к образовательному уровню подготовки – бакалавр.
Дисциплина "Мореходная астрономия" изучается на в течении двух семестров, на основе знаний, полученных по математике, физике и математических основ судовождения.
Уровень освоения дисциплины должен быть таким, чтобы обеспечить:
- знание основ сферической и общей астрономии;
- знание звездного неба (опознавание основных созвездий и навигационных звезд);
- знание устройства и умение работать с астрономическими инструментами (секстан, звездный глобус и измерители времени);
- знание основ и практическое выполнение определение поправки компаса по светилам;
- знание теоретических основ определения места по светилам;
- практическое выполнение определения места по Солнцу;
- практическое выполнение определения места по звездам.
Лабораторные работы и практические занятия курса “Мореходная астрономия” предназначены для углубления и закрепления теоретических знаний, выработки твердых практических навыков измерений и расчетов исходных данных астрономических задач, практического применения конечных результатов для обеспечения безопасности плавания судна и эффективного решения его производственных задач. Совместно с теоретическими знаниями лабораторные работы и практические занятия обеспечивают качественную подготовку студентов к сдаче комплексного Государственного экзамена по “Судовождению” после окончания летней экзаменационной сессии четвертого курса при получении диплома бакалавра и Госэкзамена по “Судовождению” при получении диплома специалиста.
В течение двух семестров изучения мореходной астрономии лабораторные работы выполняются в двух семестрах на протяжении 36 часов занятий. Изучение курса имеет основной целью подготовку студентов к успешной работе с инструментами и пособиями на предстоящей штурманской практике. При этом студенты на лекционных и лабораторных занятиях получают минимум знаний и практических навыков по решению всех основных задач мореходной астрономии. В течение последнего семестра изучения курса (последний семестр обучения студентов дневного отделения) все занятия направлены на закрепление теоретических навыков полученных ранее, доведение основных приемов решения задач до автоматизма, выработку умения контролировать результаты измерений и расчетов как на этапе завершения, так и в процессе всей работы, на развитие творческого подхода к комплексному использованию приборов и методов мореходной астрономии.
В отличие от многих уже изучавшихся студентами дисциплин мореходная астрономия оперирует немногочисленными довольно простыми приборами и пособиями, однако ее методы требуют очень высокой точности измерений и расчетов. Последнее требование выполнимо лишь за счет большой практической работы, поэтому в курсе мореходной астрономии лекционный материал по объему более чем в два раза меньше лабораторных и практических занятий. Большая значимость этого вида учебной работы студентов требует от них очень серьезного отношения к каждому занятию. Это возможно при выполнении всеми студентами следующих организационно-методических рекомендаций.
1. Залогом успешного и своевременного выполнения лабораторной работы или практического занятия является предварительная подготовка к ним путем изучения основных теоретических положений данной темы по конспекту и учебнику.
2. Своевременное выполнение лабораторных работ и практических занятий гарантирует успешную сдачу зачетов и хорошую оценку на экзамене.
3. Каждое задание лабораторных работ или практических занятий в курсе мореходная астрономия рассчитано на постоянную работу студента в течение двух академических часов, поэтому потери времени на занятиях недопустимы.
4. Торопиться при выполнении каждого занятия надо не спеша. Это очень важно при решении незнакомых трудоемких задач. Скорость решения появляется потом, сначала необходимо научиться решать задачу правильно.
5. Студент должен стараться на занятиях работать самостоятельно. То, что подскажут в процессе работы товарищи или преподаватель быстро забудется, то, что научишься сам - запомнится надолго.
6. Студент должен учиться контролировать правильность измерений и расчетов на каждом этапе. Методы и приемы мореходной астрономии позволяют это делать достаточно просто. В частности все задачи курса имеют промежуточные ответы.
9. Записи всех результатов необходимо вести карандашом, красиво и аккуратно, цифра под цифрой - это повышает точность и надежность правильного решения. Небрежные записи недопустимы.
10. На занятиях студент никогда не должен отказываться помочь товарищу, если может, разумеется помощь должна заключаться в объяснении материала, а не в решении вместо товарища. При этом помогающий очень хорошо учится и сам.
Сложность преподавания мореходной астрономии состоит в том, что она состоит из ряда совершенно не связанных друг с другом наук, это и небесная механика, и сферическая тригонометрия, и оптика, и т.д. Как правило, построение курса мореходной астрономии идёт от теории. То есть каждая наука выделена в отдельный независимый раздел, после изучения всех разделов отдельные части сливаются в конкретные полнометражные задачи.
При таком построении курса студенты хорошо усваивают теоретический материал, но с другой стороны, усвоение практического материала затрудняется. Причиной этого является то, что приходится решать абстрактные, вырванные из контекста задачи, не имеющие начала и конца. Практика показывает, что студент с большим интересом решает и лучше воспринимает конкретные задачи, имеющие практическое значение.
Конечным итогом обучения предмету, является именно умение решать сугубо практические задачи, в конце концов, штурман умеющий жонглировать сложнейшими формулами, но не знающий с какой стороны подойти к секстану это нонсенс.
В данном пособии реализуется проблемный подход подачи материала. То есть, после изложения основ мореходной астрономии перед студентом ставится полная задача по определению места судна. В дальнейшем на примере отдельных частей задачи разбирается её теоретическая подоплёка и даётся подробный алгоритм решения.
После разбора полной задачи по частям, её решение объединяется в общий алгоритм, а так же, учитывая то, что в эту задачу входят все основные «кирпичики», из которых строится большинство задач мореходной астрономии, строятся алгоритмы остальных задач.
Для удобства изложения материала, в данном пособии задачи мореходной астрономии разделены на три типа:
· Промежуточные;
· Основные;
· Вспомогательные.
Подробнее эта разделение обосновано в соответствующем параграфе.
Практическое пособие состоит из тёх частей. В первой части приводится в сжатом виде теоретическое обоснование, алгоритмы решения задач и примеры. Во второй части даются задания на лабораторные, практические занятия, а так же расчётно-графические работы и задания для студентов заочного отделения.
В задачнике даётся 14 типов задач. На каждый тип задач приводится сто вариантов (для задач на ОМС по одновременным наблюдениям двух светил даётся 300 вариантов, а для задач на ОМС по разновременным наблюдениям Солнца 200 вариантов), что даёт возможность давать каждому студенту индивидуальное задание и облегчает контроль правильности выбора задания студентом. Одна из задач на ОМС по одновременным наблюдениям двух светил является комплектной, на основании которой решается большинство вспомогательных задач.
Для облегчения решения задач в домашних условиях, в конце третьей части приводятся выдержки из Морского астрономического ежегодника на 1993г., ТВА-52, таблицы для исправления высот светил и таблицы 20а и 20б из МТ-75.
Часть 1. Методы решения задач мореходной астрономии.
Глава1. Небесная сфера. Основные понятия.
§1. Небесные системы координат.
Небесной сферой называется вспомогательная сфера произвольного радиуса, к центру которой параллельно перенесены основные линии и плоскости наблюдателя и Земли, а так же направления на светила.
Положение светила на небесной сфере определятся при помощи системы координат.
· Горизонтная система координат.
Привязана к наблюдателю, то естьявляется неподвижной относительно наблюдателя и перемещается вместе с ним (рис.1.).
• Основное направление - вертикаль или отвесная линия z-n определяется направлением силы тяжести в данной точке Земли.
• Зенит z, надир n получаются при пересечении вертикали с небесной сферой.
Основные круги:
истинный горизонт – большой круг на небесной сфере перпендикулярный отвесной линии, проходит через точки NOstSW;
• меридиан наблюдателя – проекция земного меридиана наблюдателя на небесную сферу. Проходит через точки z, n, N, S.
• Координатная сетка:
• вертикалы – большие круги проходящие через точки зенит и надир. Меридиан наблюдателя является так же и вертикалом;
• альмукантараты – круги на небесной сфере перпендикулярные отвесной линии, то есть параллельные истинному горизонту.
Координаты:
• Высота светила h – дуга вертикала светила от истинного горизонта до места светила, измеряется от 0о до ±90о, если высота меньше 0о она называется снижением –h.
• Азимут А – дуга истинного горизонта от меридиана наблюдателя до вертикала светила. Применяют три системы счёта азимута:
• Круговая – считается в пределах 0о-360о от точки N в сторону точки Ost до вертикала светила.
• Полукруговая – считается в пределах 0°-180° от точки N в северных широтах и S в южных в сторону O или W.
• Четвертная – считается в пределах 0°-90° от ближайшей части меридиана наблюдателя до меридиана светила.
• Зенитное расстояние z – дуга вертикала от зенита до места светила в пределах 0о-180о, с высотой связана соотношением z=90°-h.
· Первая экваториальная система координат.
Основное направление – ось мира представляет собой линию параллельную земной оси проходящую через центр небесной сферы. Точки пересечения оси мира с небесной сферой называются полюсами мира PN северным и PS южным.
Основные круги:
• Экватор – большой круг перпендикулярный оси мира, проходит через точки QOstQ’W.
• Меридиан наблюдателя.
Координатная сетка: параллели и меридианы.
Координаты:
• Склонение δ светила – дуга меридиана светила от небесного экватора до места светила. Считается 0о-90о в сторону N или S.
• Часовой угол t светила – дуга экватора от полуденной части меридиана наблюдателя до меридиана светила считаемая в сторону точки W. В таком счёте угол называют вестовым или обыкновенным и наименование обычно не приписывают. Помимо этого применяют полукруговой счет часовых углов 0о-180о в сторону к W или Ost.
• Полярное расстояние Δ – дуга меридиана светила от повышенного полюса до места светила, считаемая 0о-90о. Со склонением связана соотношением Δ=90о-δ.
· Вторая экваториальная система координат.
Основное направление – ось мира.
Основные круги:
• Экватор.
• Меридиан точки Овна. Точка Овна ^ или точка весеннего равноденствия расположена в пересечении эклиптики с экватором
Координатная сетка: параллели и меридианы.
Координаты: Склонение δ светила.
• Прямое восхождение α светила – дуга экватора Овна до меридиана светила считаемая 0о-360о в сторону обратную вестовым часовым углам.
• Звёздное дополнение τ светила - дуга экватора Овна до меридиана светила считаемая 0о-360о в сторону вестовых часовых углов. С прямым восхождением связана соотношением τ=360-α
• Полярное расстояние Δ – дуга меридиана светила от повышенного полюса до места светила, считаемая 0о-90о. Со склонением связана соотношением Δ=90о-δ.
§2. Приближённое решение задач на небесной сфере.
Большинство задач мореходной астрономии связанно с переходом от одной системы координат к другой, приближённо эти задачи проще всего решать при помощи построения небесной сферы (рис.1.).
1. Построение проекции небесной сферы на меридиан наблюдателя.
1. Рисуем окружность меридиана наблюдателя.
2. Через центр окружности проводим вертикальную линию зенит-надир (z-n).
3. 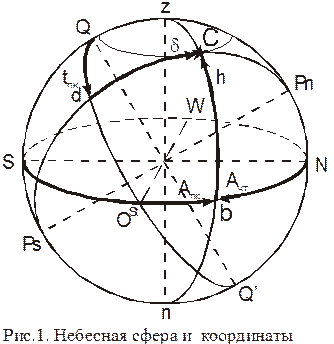 Перпендикулярно z-n, через центр окружности проводим полуденную линию NS. Положение точек N и S определяем следующим образом: если t и А западные, то точку N ставят слева, если t и А восточные, то точку N ставят справа.
Перпендикулярно z-n, через центр окружности проводим полуденную линию NS. Положение точек N и S определяем следующим образом: если t и А западные, то точку N ставят слева, если t и А восточные, то точку N ставят справа.
4. Под углом j к полуденной линии проводим ось мира PNPS, если широта северная поднимаем точку PN над точкой N, если южная над S.
5. Перпендикулярно оси мира проводим линию QQ’.
6. Между точками N и S проводим плоскость истинного горизонта, между точками Q и Q’ небесный экватор. Следим за тем, что бы дуги NS и QQ’ были одинаковы.
7. На пересечении небесного экватора и истинного горизонта наносим точки Ost и W. При дальнейших построениях не забываем, что Ost и W делят дуги NS и QQ’ по 900 несмотря на визуальное несоответствие.
Дальнейшее решение задачи распадается на шесть случаев. Первые три рассмотрим подробно:
Дано d и t, найти A и h.
1. По небесному экватору от точки Q откладываем tпк в сторону своей части света, если t круговое, то в сторону W. Получаем т. d.
2. Через PN, PS и d проводим меридиан светила.
3. От точки d в сторону PN или PS в зависимости от наименования склонения откладываем на глаз величину d и получаем точку с - положение светила на небесной сфере.
4. Через точки z, n и светило проводим вертикал светила, пересечение которого с истинным горизонтом даст точку b.
5. От точки b до светила вдоль вертикала светила снимаем высоту h.
6. Вдоль линии истинного горизонта снимаем А с наименованием.
Дано A и h, найти d и t.
1. Вдоль линии истинного горизонта наносим азимут светила в соответствии с наименованием. Получаем точку b.
2. Через точки z, n и b проводим вертикал светила.
3. От линии истинного горизонта из точки b вдоль вертикала светила наносим высоту h и получаем положение светила на небесной сфере.
4. Через PN, PS и светило проводим меридиан светила, в точке пересечения с экватором получаем т. d.
5. Вдоль небесного экватора от точки Q до точки d снимаем t.
6. Через PN, PS и d проводим меридиан светила.
7. От точки d в сторону светила снимаем величину d с наименованием.
Дано h и t, найти d и А.
1. По небесному экватору от точки Q откладываем tпк в сторону своей части света, если t круговое, то в сторону W. Получаем т. d.
2. Через PN, PS и d проводим меридиан светила.
3. Относительно т. z проводим альмукантарат с радиусом 90°-h при этом на пересечении с меридианом светила получим т. с – положение светила (при определенных условиях возможно две точки пересечения альмукантарата с меридианом), через которую проводим вертикал светила. В пересечении вертикала и истинного горизонта получим точку b от которой откладываем h.
4. Вдоль линии истинного горизонта до вертикала светила снимаем А с наименованием.
5. От точки d в сторону светила снимаем величину d с наименованием.
Решение оставшихся типов задач во многом напоминает разобранные решения и для студента освоившего их не представляет больших трудностей.
§3. Параллактический треугольник и его решение.
В различных вопросах астрономии требуется более точное решение задач на переход от одной системы координат к другим. Точные формулы, связывающие координаты можно получить, воспользовавшись закономерностями сферической тригонометрии.
Построим небесную сферу для данной широты (рис.2.) и проведём на ней меридиан и вертикал светила. В результате получится треугольник ZPNC, сторонами которого являются дуги больших кругов: меридиана наблюдателя, вертикала светила и меридиана светила. Этот треугольник, имеющий в астрономии огромное значение и применение, называется параллактическим, полярным или астрономическим треугольником светила.
Стороны этого треугольника численно равны:
•  сторона ZPN – дополнению широты до 90° (90°- j)
сторона ZPN – дополнению широты до 90° (90°- j)
• сторона PNZ – дополнению склонения до 90° (90°- d)
• сторона ZC – дополнению высоты до 90° (90°- h)
Его углы равны:
• угол при зените Z – азимуту А всегда в полукруговом счёте;
• угол при полюсе P – местному часовому углу t всегда в практическом счёте;
• угол при светиле С – называется параллактическим углом q.
Рассмотрим основные случаи решения параллактического треугольника, встречающиеся в мореходной астрономии.
Нахождение h и A светила по известным j, d и t.
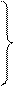 Применив к параллактическому треугольнику формулы косинуса стороны и котангенсов, получим:
Применив к параллактическому треугольнику формулы косинуса стороны и котангенсов, получим:
|

После упрощения и отделения неизвестных получим окончательно:
|

В этой системе значительно снижается точность вычисления А при часовых углах близких к 90°. Система достаточно громоздка, но азимут получается сразу в полукруговом счёте. Первая буква наименования всегда одноимённа с широтой, вторая с часовым углом в практическом счёте.
 Зачастую азимут находится из теоремы синусов:
Зачастую азимут находится из теоремы синусов:
|

Во второй системе формула для азимута зависима от h и включает в себя все ошибки вычислений. Азимут получается в четвертном счёте.
В некоторых случаях может применяться система:
|

Система формул более точна, чем предыдущая особенно при высотах более 30°, так же эту систему не надо анализировать на знаки.
Нахождение d и t светила по известным j, h и A.
Применив к параллактическому треугольнику формулы косинуса стороны и котангенсов, после упрощений получим:
|


Кроме этих основных вариантов перехода от одной системы к другой возможны и другие различные случаи.
Решение этих систем реализуется при помощи различных специальных таблиц, устройство которых будет разбираться позднее, а так же при помощи вычислительной техники.
Глава2. Основные задачи Мореходной астрономии
§4. Классификация задач.
Условно задачи, решаемые в курсе «Мореходная астрономия» можно разделить на три категории:
Основные задачи, к которым относятся задачи на Определение Места Судна (ОМС ), и задачи на определение поправки компаса.
Вспомогательные задачи, служащие для определения дополнительных параметров, используемых для облегчения, ускорения и контроля решения основных задач. К этой категории можно отнести задачи на расчёт восхода, захода и кульминации светил; определение наименования светил и подбор светил на заданный момент наблюдений при помощи звёздного глобуса; задачи на перевод времени; расчёт точности навигационных параметров и пр.
К этой же категории можно отнести и задачи на вспомогательной небесной сфере рассмотренные в предыдущем параграфе.
Промежуточные задачи. Понятие промежуточных задач вводится в данном практическом курсе, для облегчения понимания решения основных задач. Каждая такая задача, представляя собой теоретически и математически законченный модуль, является как бы кирпичиком, из которых строится решение основных и вспомогательных задач. Эти задачи являются совершенно разнородными с точки зрения теории, и обоснованию каждой такой задачи может быть посвящён целый раздел теоретического курса. На практике же эти задачи решаются совместно, дополняя друг друга.
К этим задачам можно отнести задачи на перевод времени; расчёт склонений и часовых углов светил; расчёт счислимых азимута и высоты светила; исправление высот светил; отыскание вероятнейшего места судна и пр.
Ещё раз хотим напомнить, что такое разделение задач является весьма условным, и вводится для облегчения понимания курса.
§5. Основные величины и понятия, используемые при решении задач.
Измеряемые величины. Величины, снимаемые с отсчётных устройств различных приборов в процессе наблюдений. К ним относятся:
• ОС – Отсчёт Секстана. Величина, снимаемая с отсчётного устройства навигационного секстана с точностью до 0.1¢.
• КП – Компасный Пеленг светила. Величина, снимаемая при помощи пеленгатора с репитера компаса с точностью до 0.1°.
• ТС – судовое время. Снимается с судовых часов в момент наблюдений с точностью до 1м. (Полное определение понятия времени даётся в § 11 данного пособия.
• ТХР – время хронометра. Снимается с хронометра в момент наблюдений с точностью до 1с.
• ТГР – Гринвичское время. Получается путём исправления ТХР поправкой хронометра UХР.
Табличные величины. Выбираются или рассчитываются при помощи таблиц или пособий. Характеризуют наблюдаемый объект, в курсе мореходной астрономии – светило.
• tгр – Гринвичский часовой угол светила. Рассчитывается при помощи МАЕ для долготы Гринвича на заданную дату и время.
• tм – местный часовой угол светила. Рассчитывается при помощи МАЕ для счислимой долготы на заданную дату и время. Совместно с jС и d используется для расчёта hC и АС.
• d - склонение светила. Рассчитывается при помощи МАЕ на заданную дату и время.
(Общие определения часового угла и склонения приведены в §1 данного пособия).
Счислимые величины. Являются результатом ведения навигационной прокладки (счисления). Учитывая то, что во время движения на судно действует большое количество разнородных факторов, влияние которых полностью учесть невозможно, результаты счисления весьма приблизительны и должны периодически уточняться обсервациями.
• jС, lС - счислимые координаты судна (широта и долгота). Снимаются с карты на момент обсервации. (Полное определение координат даётся в курсе «Навигация»).
• hC – счислимая высота светила. Рассчитывается при помощи систем формул сферической тригонометрии, или при помощи специальных таблиц (ТВА-57, ВАС-58) для счислимого места судна. (Полное определение высоты светила даётся в §1 данного пособия).
• АС – счислимый азимут светила. Рассчитывается при помощи систем формул сферической тригонометрии, или при помощи специальных таблиц (ТВА-57, ВАС-58) для счислимого места судна, как правило, совместно с hC.
Обсервованные величины. Получаются из непосредственных наблюдений, или путём математической обработки измерений различных навигационных параметров, т.е. параметров объектов, местоположение которых нам известно с достаточно высокой точностью. В курсе мореходной астрономии к ним относятся:
• j0, l0 - обсервованные координаты судна (широта и долгота). Являются результатом решения задачи на ОМС. С известной погрешностью принимаются нами за реальные координаты. Эта погрешность зависит от точности измерений и обработки результатов измерений.
• h0 – обсервованная высота светила. Получается из ОС (отсчёта секстана) путём исправления оного различными поправками.
Разумеется, что в этом параграфе определены лишь самые основные величины, используемые при решении задач. В процессе решения задач будет использоваться большое количество вспомогательных величин определения, которых будут вводиться по мере изложения материала.
§6. Обоснование определения места судна астрономическими методами. Различные способы ОМС.
Общие положения.
Предположим, что наблюдатель находящийся в точке М (рис.3.) на Земле, местоположение которой нам точно не известно, наблюдает светило С1 под углом h (высота светила) к истинному горизонту. Логично[1] предположить, что светило на этой же высоте будет наблюдаться в любой точке окружности проходящей через точку М и с центром в точке А являющейся проекцией светила на земную поверхность. Точку А назовём центром освещения светила, а окружность кругом равных высот. То есть наблюдатель может находиться в любой точке круга равных высот. Сферический радиус окружности будет равен зенитному расстоянию светила z= 90°–h.
Из последнего утверждения следует важный практический вывод, если измерить высоту светила h1, вычислить его зенитное расстояние z и провести на земной поверхности окружность радиусом равную полученному зенитному расстоянию, то можно утверждать, что судно находится на этом круге равных высот. Так как одна окружность не определяет места судна, необходимо измерить высоту второго светила С2, вычислить z2 и провести второй круг равных высот. На втором круге равных высот судно так же может находиться в любой точке. Обе окружности пересекутся в двух точках. В одной из них и будет находиться наше судно. Учитывая то, что расстояние между точками пересечения большие, а счислимые координаты нам известны, выбирается ближайшая к счислимым координатам точка. Координаты полюсов освещения определяются следующим образом: географическая широта равна склонению j = d, географическая долгота равна гринвичскому часовому углу светила l = tгр.
Date: 2015-10-18; view: 1708; Нарушение авторских прав