
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цепи синусоидального тока, их состав и свойства
|
|
В состав простых цепей тока входят:
– резисторные элементы (содержат, как правило, только активное сопротивление r);
– катушки индуктивности (имеют наряду с небольшим активным сопротивлением и реактивное, иногда приходится учитывать и влияние ёмкости);
– конденсаторы (обладают реактивным сопротивлением хс, с небольшими потерями энергии).
В цепях переменного тока происходят процессы (при изменении u и i) с изменениями магнитных электрических полей (в катушках индуктивности и конденсаторах).
Основные физические законы для постоянного тока справедливы и для переменного, но только для мгновенных значений (i, u, e).
В дальнейшем мы будем рассматривать цепи с сосредоточенными параметрами, то есть цепи, для которых считается, что сопротивления индуктивности и ёмкости сосредоточены на отдельных участках цепи.
Цепь с резисторным элементом представлена на рис. 2.14.
| ur |
| u |
| r |
| i |
Рис.2.14
На схеме: i, u – условные положительные направления токов и напряжений (принимаются только для взаимной ориентировки направлений i, u); r – активное сопротивление в цепи переменного тока;
 – напряжение, на которое подключена цепь.
– напряжение, на которое подключена цепь.
По закону Ома 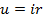 .
.
Отсюда 
где 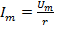 – амплитуда тока.
– амплитуда тока.
Действующее значение тока определяется
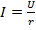 .
.
Аналогично комплексный ток
 .
.
Из выражения  видно, что ток и напряжение совпадают по фазе, т.е. временная диаграмма будет как на рис. 2.15,а.
видно, что ток и напряжение совпадают по фазе, т.е. временная диаграмма будет как на рис. 2.15,а.
Векторная диаграмма представлена на рис. 2.15,б.
| а) |
| u, i |
| u |
| i |
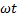
|
| U |
| I |
| б) |
Рис. 2.15
Цепь с катушкой индуктивности представлена на рис. 2.16
| UL |
| U |

|
| i |
| L |
Рис. 2.16
На схеме изображены L – индуктивность катушки, L= const;  – ЭДС самоиндукции, которая по закону Ленца противодействует сопротивлению тока (его увеличению или уменьшению).
– ЭДС самоиндукции, которая по закону Ленца противодействует сопротивлению тока (его увеличению или уменьшению).
Если к цепи приложим напряжение u, то по ней потечет ток
 ,
,
продифференцируя, получим:

ЭДС самоиндукции определим как:
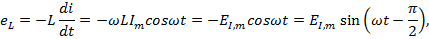
где  – амплитуда ЭДС самоиндукции.
– амплитуда ЭДС самоиндукции.
Следовательно, ЭДС самоиндукции  отстает по фазе от тока на угол
отстает по фазе от тока на угол  , так как
, так как  .
.
Напряжение на зажимах цепи будет
 ,
,
где  – амплитуда напряжения.
– амплитуда напряжения.
Напряжение на зажимах цепи опережает ток на угол  .
.
По аналогии с амплитудными значениями действующие значения напряжений и тока определяются как:
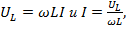
где  - индуктивное сопротивление цепи,
- индуктивное сопротивление цепи, 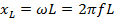 .
.
В символическом виде, если  , то
, то
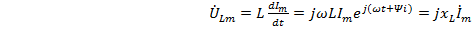 .
.
Комплексные действующие значения напряжений и тока определяются как:
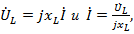
где  – комплексное индуктивное сопротивление.
– комплексное индуктивное сопротивление.
Временная и векторная диаграммы показаны на рис. 2.17,а,б соответственно.
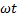
|

|

|

|

|

|

|

|
| а) |
| б) |

|

|

|
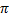
|
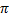 /2
/ /2
/
|
Рис. 2.17
ЭДС самоиндукции 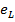 и приложенное напряжение
и приложенное напряжение  находятся в противофазе.
находятся в противофазе.
Цепь с конденсатором представлена на рис. 2.18.
| Uс |
| U |
| i |
| С |
| ~ |
Рис. 2.18
В этой цепи при увеличении U ток i – зарядный, при уменьшении U ток I – разрядный.
Мгновенное значение тока  .
.
Из функции видно  c,
c,
где  – заряд конденсатора;
– заряд конденсатора; 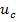 – напряжение на конденсаторе; с – ёмкость конденсатора.
– напряжение на конденсаторе; с – ёмкость конденсатора.
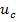 меняется по синусоидальному закону, если
меняется по синусоидальному закону, если  ,
,
тогда  ,
,
где  – амплитуда тока.
– амплитуда тока.
Ток опережает напряжение на угол  .
.
Запишем выражение для ёмкостного сопротивления цепи
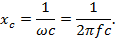
Тогда амплитуда значения тока определяется как

Для действующих значений напряжения и тока:

Комплексный амплитудный ток:

где 
Комплексные действующие значения напряжения и тока:
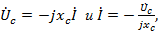
где  – комплексное ёмкостное сопротивление; -j определяет поворот вектора напряжения на угол
– комплексное ёмкостное сопротивление; -j определяет поворот вектора напряжения на угол  , то есть против вращения векторов.
, то есть против вращения векторов.
Временная и векторная диаграммы показаны на рис. 2.19 а, б соответственно.
| б) |
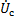
|

|

|
| а) |
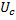
|
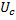 ,i ,i
|

|

|

|
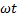
|
Рис. 2.19
Цепь переменного тока в общем случае может содержать резистор, катушку индуктивности и конденсатор, соединенные между собой последовательно или параллельно. В действительности цепь является сложным смешанным соединением этих трёх элементов, так как каждый элемент цепи реально обладает не одним, а двумя-тремя свойствами. К примеру, активное сопротивление может быть полностью или частично сопротивлением катушки индуктивности, отдельно взятая ёмкость может быть ёмкостью между проводами сети, каждая катушка индуктивности, помимо собственных свойств, частично обладает свойствами резистора и конденсатора.
Неразветвленная цепь переменного тока – это цепь, состоящая из последовательно соединённых участков с активным сопротивлением r, индуктивностью L и ёмкостью С (рис. 2.20).
| ~ |
| u |
| i |
| r |
| L |
| C |

|
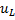
|
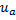
|
Рис. 2.20
Приложенное к такой цепи напряжение u=  вызовет в ней ток
вызовет в ней ток 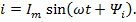 Напряжение u состоит из трёх слагаемых: активного напряжения ua, совпадающего по фазе с током i, индуктивного напряжения uL, опережающего ток на угол
Напряжение u состоит из трёх слагаемых: активного напряжения ua, совпадающего по фазе с током i, индуктивного напряжения uL, опережающего ток на угол  , и ёмкостного напряжения uc, отстающего от тока на
, и ёмкостного напряжения uc, отстающего от тока на  . Покажем это аналитически и графически.
. Покажем это аналитически и графически.
По второму закону Кирхгофа можно записать:

где  - мгновенные значения напряжений и тока в цепи.
- мгновенные значения напряжений и тока в цепи.
В данном случае при расчете цепи мы будем определять ток после окончания переходного процесса, когда в цепи будет протекать установившийся переменный ток. Следует отметить, что реально после включения цепи, то есть подачи напряжения 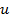 , в течение относительно малого промежутка времени происходит переходный процесс, характеризующийся особым состоянием цепи переменного тока. Естественно при корректном исследовании это требует общего решения, которое здесь не рассматривается. Мы найдем только частное решение уравнения для установившегося тока.
, в течение относительно малого промежутка времени происходит переходный процесс, характеризующийся особым состоянием цепи переменного тока. Естественно при корректном исследовании это требует общего решения, которое здесь не рассматривается. Мы найдем только частное решение уравнения для установившегося тока.
Частным решением является выражение синусоидального тока
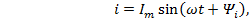
для которого нужно найти амплитуду  и фазовый угол
и фазовый угол  или угол сдвига по фазе
или угол сдвига по фазе 
Если ток цепи i изменяется по гармоническому закону, то напряжения на участках цепи 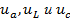 изменяются по этому же закону. Временная диаграмма напряжений и токов в установившемся режиме при последовательном соединении резистора, катушки индуктивности и конденсатора показа на рис. 2.21.
изменяются по этому же закону. Временная диаграмма напряжений и токов в установившемся режиме при последовательном соединении резистора, катушки индуктивности и конденсатора показа на рис. 2.21.

|

|

|

|

|
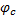
|

|
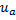
|

|
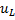
|

|
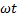
|
Рис. 2.21
На основании уравнения для мгновенных значений, составленного по второму закону Кирхгофа, можно написать уравнения в символическом виде:
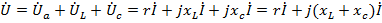 =
=  ,
,
где  - комплексные напряжения и ток, отображающие их действующие значения;
- комплексные напряжения и ток, отображающие их действующие значения;
 – комплексное индуктивное сопротивление;
– комплексное индуктивное сопротивление;
 – комплексное ёмкостное сопротивление;
– комплексное ёмкостное сопротивление;
 – комплексное полное сопротивление цепи (обозначается большой буквой и состоит из вещественной и мнимой частей).
– комплексное полное сопротивление цепи (обозначается большой буквой и состоит из вещественной и мнимой частей).
В соответствии с этим уравнением построим векторную диаграмму (рис. 2.22).
Исходный вектор  направим вертикально вверх (выбор его направления, в принципе, является произвольным). Все векторы будем изображать в заранее принятом масштабе. В фазе с вектором тока
направим вертикально вверх (выбор его направления, в принципе, является произвольным). Все векторы будем изображать в заранее принятом масштабе. В фазе с вектором тока 
 находится вектор активной составляющей напряжения
находится вектор активной составляющей напряжения 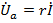 .
.
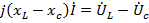
|
| F |

|
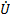
|
| B |

|

|
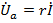
|
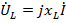
|
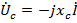
|
- 
|

|

|
Рис. 2.22
Под углом  в сторону опережения относительно вектора
в сторону опережения относительно вектора 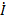 (против часовой стрелки) направим вектор индуктивной составляющей напряжения
(против часовой стрелки) направим вектор индуктивной составляющей напряжения 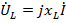 , а под углом
, а под углом  в сторону отставания (по часовой стрелке) – вектор ёмкостной составляющей напряжения
в сторону отставания (по часовой стрелке) – вектор ёмкостной составляющей напряжения 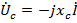 . Геометрическая сумма всех векторов действующих величин
. Геометрическая сумма всех векторов действующих величин  определит вектор действующего напряжения
определит вектор действующего напряжения  на зажимах цепи.
на зажимах цепи.
Из прямоугольного треугольника OBF по закону Пифагора запишем для действующих параметров в обычной комплексной форме:
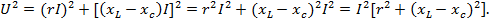
Отсюда определим действующее значение тока в цепи:
 .
.
Полученное выражение для  формально подобно выражению закона Ома для цепи постоянного тока. Сдвиг по фазе
формально подобно выражению закона Ома для цепи постоянного тока. Сдвиг по фазе  между током и напряжением определяется выражением:
между током и напряжением определяется выражением:
 ,
,
где  – реактивное сопротивление цепи;
– реактивное сопротивление цепи;
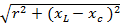 – полное сопротивление цепи.
– полное сопротивление цепи.
Если в цепи преобладает индуктивное сопротивление ( , а реактивное сопротивление х выражается положительным числом (
, а реактивное сопротивление х выражается положительным числом ( , то разность фаз напряжения и тока положительна (
, то разность фаз напряжения и тока положительна (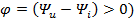 и напряжение цепи опережает ток (рис.2.23).
и напряжение цепи опережает ток (рис.2.23).
| φ=(-Ψu-Ψi)=(-Ψu) Ψi=0; φ<0 |
| а) |
| u,i |
| u |
| i |
| 0 |
| φ=-Ψu |
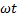
|
| б) |

|
-jx 
|
jxL 
|
| 0 |
r 
|
| φ |
-jxL 
|
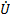
|

|
Рис. 2.23
Если же в цепи преобладает ёмкостное сопротивление ( , реактивное сопротивление выражается отрицательным числом (
, реактивное сопротивление выражается отрицательным числом ( , то разность фаз отрицательна (
, то разность фаз отрицательна ( и ток в цепи опережает напряжение (рис. 2.24).
и ток в цепи опережает напряжение (рис. 2.24).
При численном равенстве ёмкостного и индуктивного сопротивлений (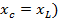 реактивное сопротивление в цепи отсутствует (
реактивное сопротивление в цепи отсутствует (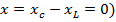 , ток и напряжение совпадают по фазе (
, ток и напряжение совпадают по фазе ( . Временная и векторная диаграммы изображены на рис. 2.24, а и б соответственно.
. Временная и векторная диаграммы изображены на рис. 2.24, а и б соответственно.
| а) |
| u,i |
| u |
| i |
| φ=0 |
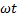
|
-jxL 
|
jxL 
|
| б) |

|
r 
|
Рис. 2.24
Следовательно, в цепях с индуктивностью и ёмкостью угол сдвига по физе  между напряжением и током может изменяться в пределах от
между напряжением и током может изменяться в пределах от  ,
,
то есть 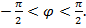
Для комплексных действующих напряжений можно написать выражения, аналогичные закону Ома:

где Z – комплексное полное сопротивление цепи в символическом виде.
Date: 2015-10-21; view: 758; Нарушение авторских прав