
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Представление переменного тока в символическом виде
|
|
Расчёт цепей переменного тока может производиться не только графическим построением векторных диаграмм, но и аналитически – операциями с комплексными числами, символически изображающими синусоидальные ЭДС и токи. Достоинством рассмотренного метода векторных диаграмм при исследовании цепей переменного тока является наглядность, а недостатком - малая точность графических построений.
Применение символического метода обеспечивает выполнение расчётов цепей с большей точностью, быстро и практически безошибочно, так как оперирование только с символами и числами позволяет широко использовать вычислительную технику. Поэтому решение задач с помощью символического метода имеет особые преимущества при рассмотрении сложных цепей переменного тока.
Если гармонические напряжения, токи и ЭДС можно изображать вращающимися векторами, а векторы - комплексными числами, то и гармонические напряжения, токи и ЭДС можно в свою очередь изображать комплексными числами.
Предположим, к примеру, что мгновенное напряжение u определяется выражением 
Это переменное напряжение  графически изображается вектором длиной
графически изображается вектором длиной  (в выбранном масштабе), вращающимся против часовой стрелки с угловой скоростью
(в выбранном масштабе), вращающимся против часовой стрелки с угловой скоростью  (его численное значение
(его численное значение 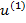 определяется проекцией вектора
определяется проекцией вектора  на вертикальную ось ординат векторной диаграммы, а
на вертикальную ось ординат векторной диаграммы, а 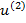 -проекцией на горизонтальную ось абсцисс). Вектор с модулем
-проекцией на горизонтальную ось абсцисс). Вектор с модулем  и аргументом
и аргументом  символически можно изобразить в виде комплексного числа
символически можно изобразить в виде комплексного числа  в алгебраической, показательной и тригонометрической формах.
в алгебраической, показательной и тригонометрической формах.
Алгебраическая форма комплексного числа  представляется в виде:
представляется в виде:
 ,
,
где j =  – единичное мнимое число;
– единичное мнимое число;
 - вещественная часть комплексного числа,
- вещественная часть комплексного числа,
 ;
;
 - мнимая часть комплексного числа,
- мнимая часть комплексного числа,
 ;
;
 – аргумент комплексного числа,
– аргумент комплексного числа,
 ;
;
 - модуль комплексного числа,
- модуль комплексного числа,
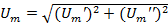 .
.
Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повёрнута по отношению к вещественной на угол  в положительном направлении (против часовой стрелки).
в положительном направлении (против часовой стрелки).
Комплексное число  геометрически можно изобразить на комплексной плоскости с осями координат, представляющими вещественную и мнимую части числа. При этом положительная вещественная ось +1 для удобства направлена вправо, а ось мнимых чисел j – вверх от оси вещественной (рис. 2.12).
геометрически можно изобразить на комплексной плоскости с осями координат, представляющими вещественную и мнимую части числа. При этом положительная вещественная ось +1 для удобства направлена вправо, а ось мнимых чисел j – вверх от оси вещественной (рис. 2.12).
| + j |
| + 1 |

|

|

|

|
Рис. 2.12
Здесь изображен на комплексной плоскости вектор  , имеющий модуль
, имеющий модуль 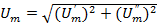 и аргумент
и аргумент  . Вещественная часть комплексного числа
. Вещественная часть комплексного числа  , отображающего символическое выражение вектора амплитуды напряжения, представлена отрезком
, отображающего символическое выражение вектора амплитуды напряжения, представлена отрезком  на вещественной оси +1, а мнимая – отрезком
на вещественной оси +1, а мнимая – отрезком  на мнимой оси j. Каждому численному значению амплитуды напряжения (а также тока и ЭДС) на комплексной плоскости соответствуют только одна точка и только один вектор, проведённый из начала координат в эту точку. Векторы, которые выражаются комплексными числами, обозначаются соответственным буквенным символом напряжения, токи и ЭДС с точкой наверху.
на мнимой оси j. Каждому численному значению амплитуды напряжения (а также тока и ЭДС) на комплексной плоскости соответствуют только одна точка и только один вектор, проведённый из начала координат в эту точку. Векторы, которые выражаются комплексными числами, обозначаются соответственным буквенным символом напряжения, токи и ЭДС с точкой наверху.
При сложении комплексных чисел, соответствующих синусоидальным напряжениям, ЭДС и токам, получаются комплексные числа, изображающие геометрические суммы складываемых векторов. На рис. 2.13 показано сложение двух комплексных чисел 
| +j |
| +1 |
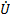 1m 1m
|
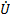 2m 2m
|
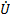 mΣ= mΣ= 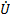 1m+ 1m+ 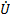 2m 2m
|

|

|
 + +  = = 
|

|

|
 + +  = = 
|
Рис. 2.13
При сложении двух комплексных чисел
 и
и  комплексное число
комплексное число 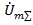 , соответствующее их сумме, будет:
, соответствующее их сумме, будет:
 )
)
Вещественной частью такого числа является  ,
,
а мнимой –  .
.
Вектор, соответствующий полному комплексному числу 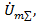 находится геометрическим сложением векторов
находится геометрическим сложением векторов 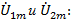

Умножать или делить комплексные числа обычно более удобно, преобразовав их в показательную форму. Вектор с модулем  символически изображается в показательной форме в виде:
символически изображается в показательной форме в виде:

где e=2,718- постоянное число.
Обычно в символических выражениях гармонически изменяющихся параметров, представленных в показательной форме, отбрасывается переменный аргумент 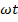 , одинаковый для всех напряжений, ЭДС и токов одной и той же частоты. Это соответствует тому, что в дальнейшем рассматриваются уже не вращающиеся, а неподвижные вектора. В этом случае символическое выражение амплитуды напряжения запишется:
, одинаковый для всех напряжений, ЭДС и токов одной и той же частоты. Это соответствует тому, что в дальнейшем рассматриваются уже не вращающиеся, а неподвижные вектора. В этом случае символическое выражение амплитуды напряжения запишется:
 ,
,
а для действующего значения напряжения соответственно получим
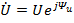
При умножении двух комплексных чисел 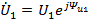 и
и  , записанных символически в показательной форме, их модуля
, записанных символически в показательной форме, их модуля  перемножаются, а аргументы
перемножаются, а аргументы  складываются. Таким образом, при умножении
складываются. Таким образом, при умножении  получаем
получаем

При делении комплексных чисел модули делятся, а аргументы вычитаются:

Комплексное напряжение  можно выразить в тригонометрической форме:
можно выразить в тригонометрической форме:

Реально существующие напряжения, ЭДС и токи выражаются вещественными числами, поэтому мгновенные значения гармонических переменных определяются вещественной частью комплексного числа. Так, для напряжения получим

Date: 2015-10-21; view: 1252; Нарушение авторских прав