
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 5
|
|
Исходные данные распределения добавленной стоимости по отраслям экономики в ЕС в 2002 г. (выбрать любую из пар зависимого и независимого показателей).

1. Методом наименьших квадратов по табличным данным найти аппроксимирующие (приближаемые) функции, то есть регрессии: линейную, квадратичную, показательную, гиперболическую.
2. В каждом случае найти общую ошибку и среднюю ошибку аппроксимации. Указать функцию лучшей аппроксимации.
3. Построить линии регрессии на одной плоскости вместе с исходными данными.
Таблицу можно считать функцией, заданной таблично.
Решение.
1. Методом наименьших квадратов по табличным данным найдем аппроксимирующие (приближаемые) функции, то есть регрессии:
а) линейную, б) квадратичную, в) показательную, г) гиперболическую.
а) определим систему нормальных уравнений для нахождения оценок параметров линейной регрессии:
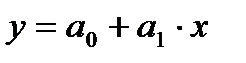 .
.

Для удобства расчетов представим таблицу исходных данных следующим образом:
| № | Государство | Промышленность, млрд. дол., х | Сельское хозяйство, млрд. дол., y | х2 | х*у |
| Венгрия | 30,7 | 3,7 | 942,49 | 113,59 | |
| Кипр | 20,3 | 4,1 | 412,09 | 83,23 | |
| Латвия | 24,7 | 4,7 | 610,09 | 116,09 | |
| Литва | 30,5 | 7,1 | 930,25 | 216,55 | |
| Мальта | 28,1 | 2,8 | 789,61 | 78,68 | |
| Польша | 3,1 | 900,00 | 93,00 | ||
| Сумма | 164,30 | 25,50 | 4 584,53 | 701,14 |
Получим систему нормальных уравнений для линейной регрессии:
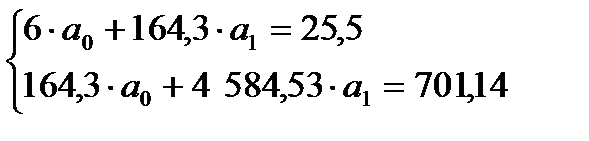
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
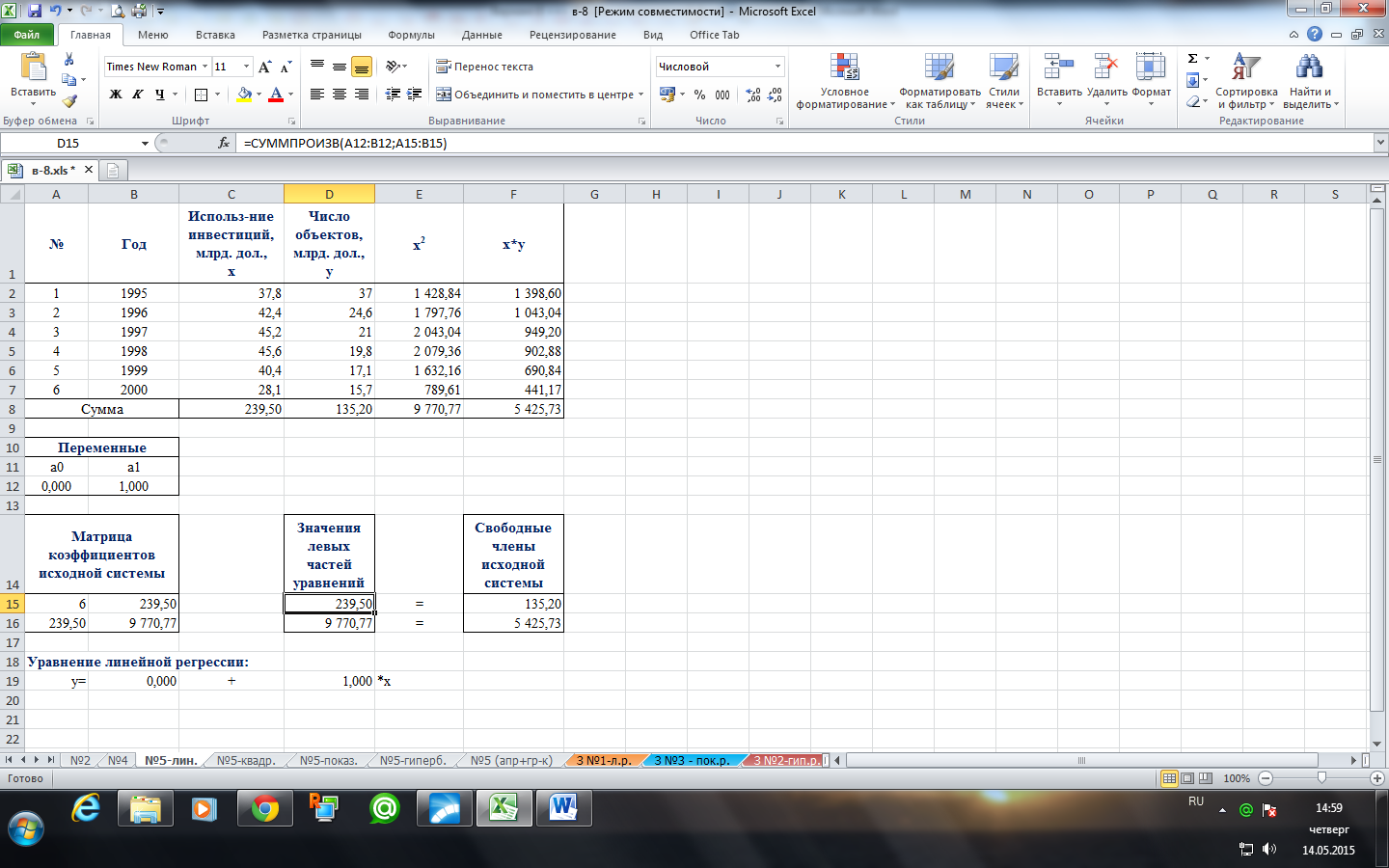

В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений 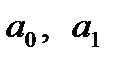 , во вторую строку записываем произвольные числовые значения 0 и 1.
, во вторую строку записываем произвольные числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных 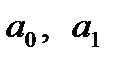 .
.
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных  »; «диапазон первой строки матрицы коэффициентов исходной системы»).
»; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
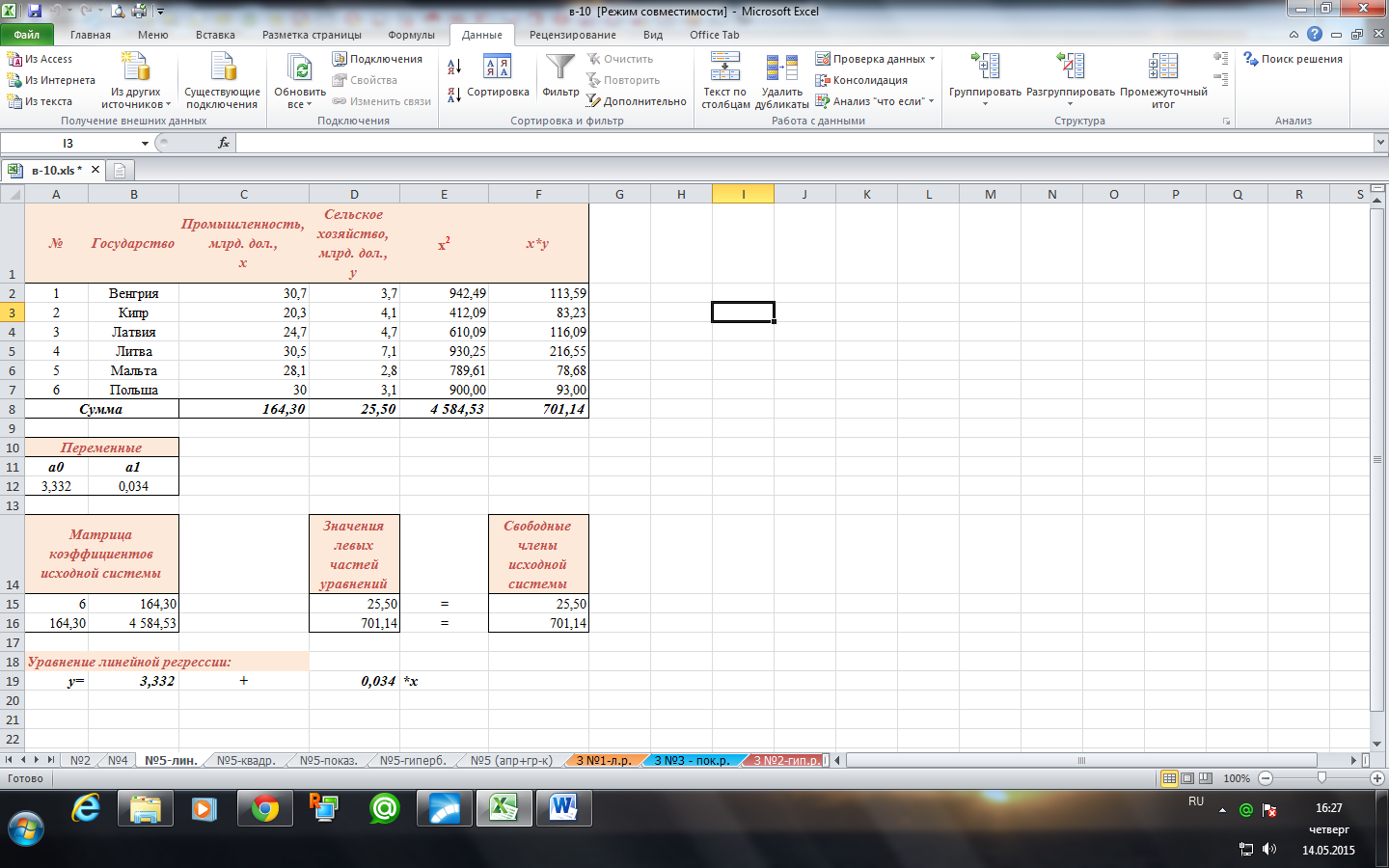
Запишем уравнение полученной линейной регрессии:
 .
.
б) определим систему нормальных уравнений для нахождения оценок параметров квадратичной регрессии:
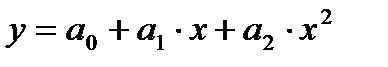 - параболы второй степени.
- параболы второй степени.
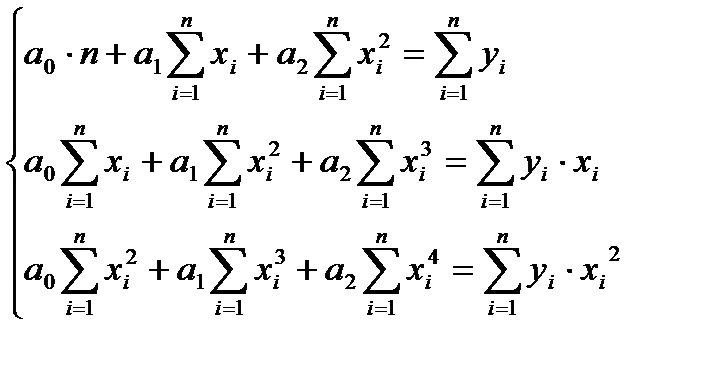
Составим вспомогательную таблицу и произведем расчеты, необходимые для составления системы нормальных уравнений.
| № | Государство | Промышленность, млрд. дол., х | Сельское хозяйство, млрд. дол., y | х2 | х3 | х4 | х*у | х2*у |
| Венгрия | 30,7 | 3,7 | 942,49 | 28 934,44 | 888 287,40 | 113,59 | 3 487,21 | |
| Кипр | 20,3 | 4,1 | 412,09 | 8 365,43 | 169 818,17 | 83,23 | 1 689,57 | |
| Латвия | 24,7 | 4,7 | 610,09 | 15 069,22 | 372 209,81 | 116,09 | 2 867,42 | |
| Литва | 30,5 | 7,1 | 930,25 | 28 372,63 | 865 365,06 | 216,55 | 6 604,78 | |
| Мальта | 28,1 | 2,8 | 789,61 | 22 188,04 | 623 483,95 | 78,68 | 2 210,91 | |
| Польша | 3,1 | 900,00 | 27 000,00 | 810 000,00 | 93,00 | 2 790,00 | ||
| Сумма | 164,30 | 25,50 | 4 584,53 | 129 929,76 | 3 729 164,39 | 701,14 | 19 649,89 |
На основании полученных результатов расчета коэффициентов система нормальных уравнений примет вид:

Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
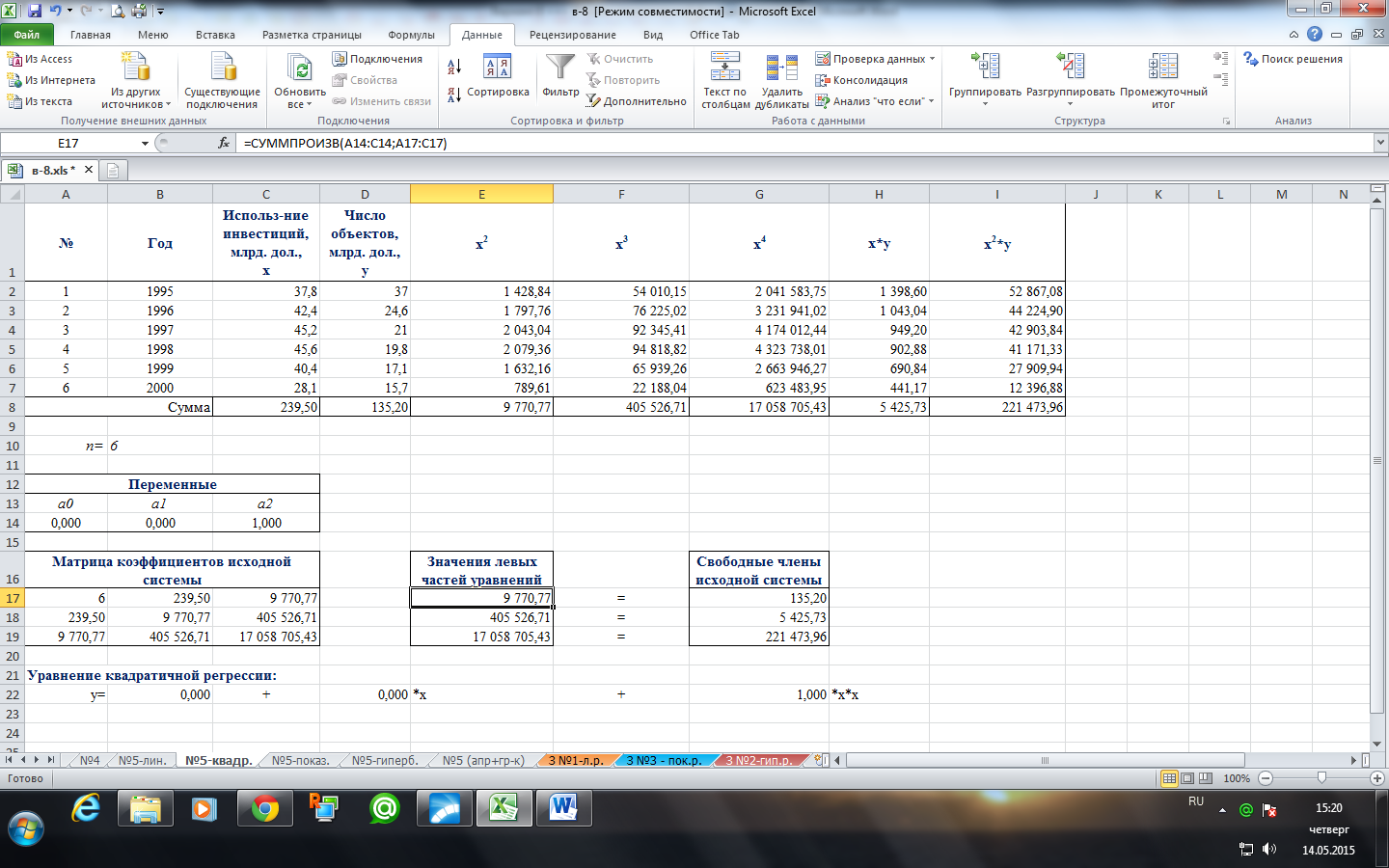

В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений  , во вторую строку записываем произвольные числовые значения 0, 0 и 1.
, во вторую строку записываем произвольные числовые значения 0, 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных 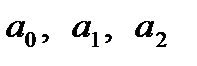 .
.
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных 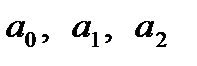 »; «диапазон первой строки матрицы коэффициентов исходной системы»).
»; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
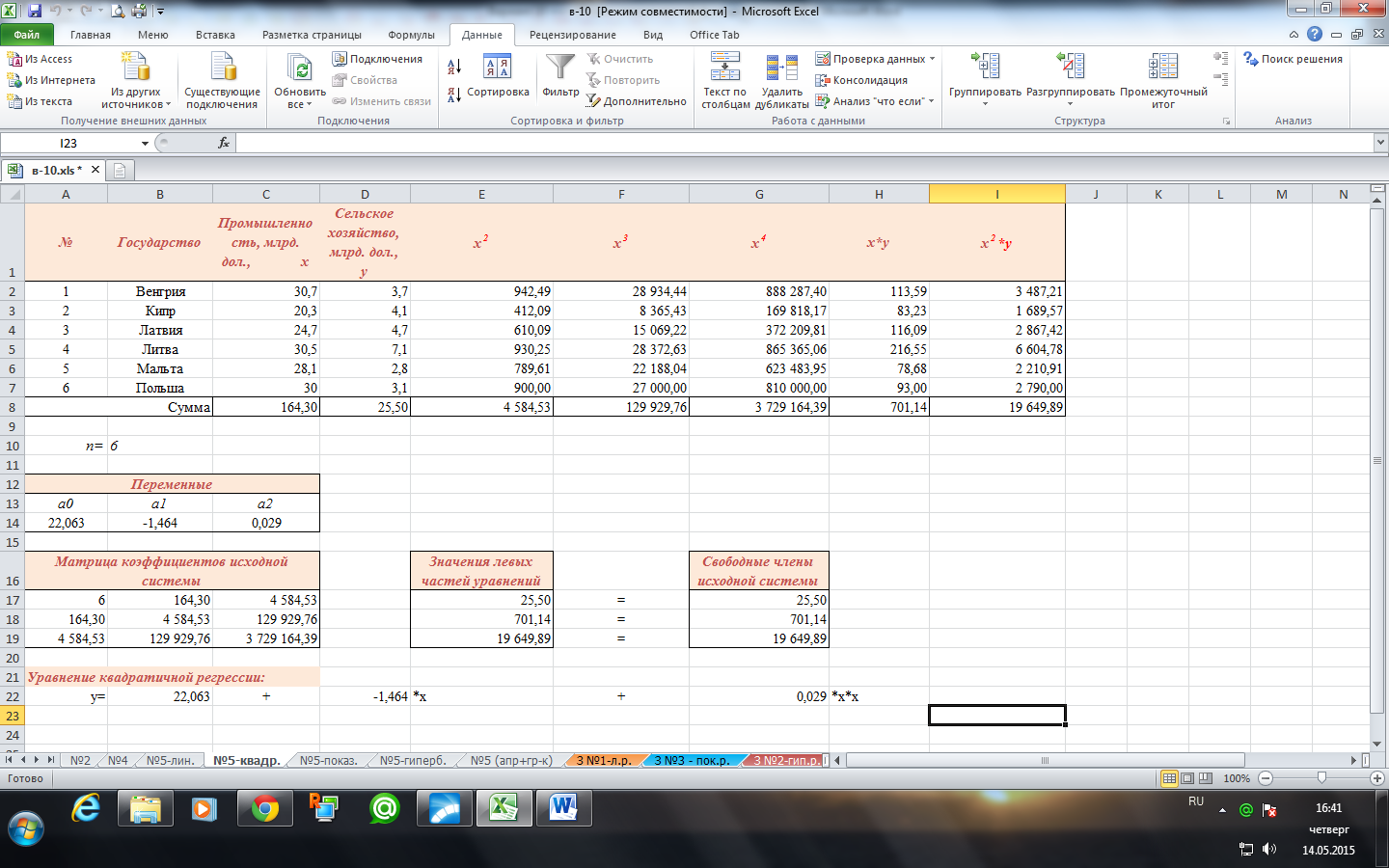
Запишем уравнение полученной квадратичной регрессии:
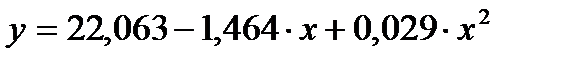 .
.
в) показательная регрессия сводится к нахождению уравнения вида:
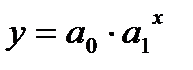
Логарифмирование данного уравнения по основанию е приводит к линейному уравнению вида: 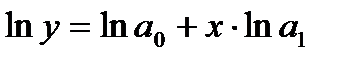 .
.
Соответственно оценки параметров  могут быть найдены методом наименьших квадратов. Для упрощения и наглядности решения произведем следующие замены переменных:
могут быть найдены методом наименьших квадратов. Для упрощения и наглядности решения произведем следующие замены переменных: 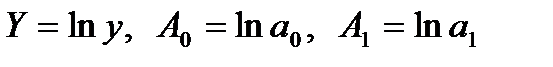 .
.
Тогда уравнение в новых переменных будет иметь вид:
 .
.
Определим систему нормальных уравнений для нахождения оценок параметров полученной линейной регрессии.
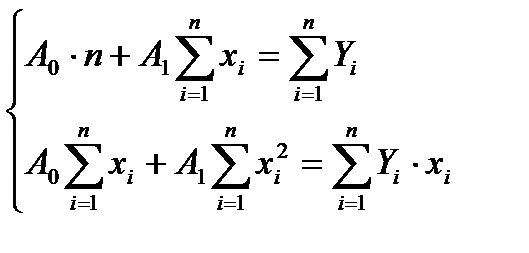
Составим таблицу для расчетов необходимых значений:
| № | Государство | Промышленность, млрд. дол., х | Сельское хозяйство, млрд. дол., y | Y | x*Y | х2 |
| Венгрия | 30,7 | 3,7 | 1,31 | 40,17 | 942,49 | |
| Кипр | 20,3 | 4,1 | 1,41 | 28,64 | 412,09 | |
| Латвия | 24,7 | 4,7 | 1,55 | 38,22 | 610,09 | |
| Литва | 30,5 | 7,1 | 1,96 | 59,78 | 930,25 | |
| Мальта | 28,1 | 2,8 | 1,03 | 28,93 | 789,61 | |
| Польша | 3,1 | 1,13 | 33,94 | 900,00 | ||
| Сумма | 164,30 | 25,50 | 8,39 | 229,69 | 4 584,53 |
Получим систему нормальных уравнений для линейной регрессии:
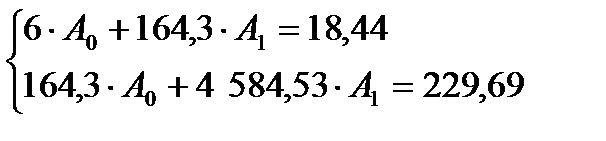
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.

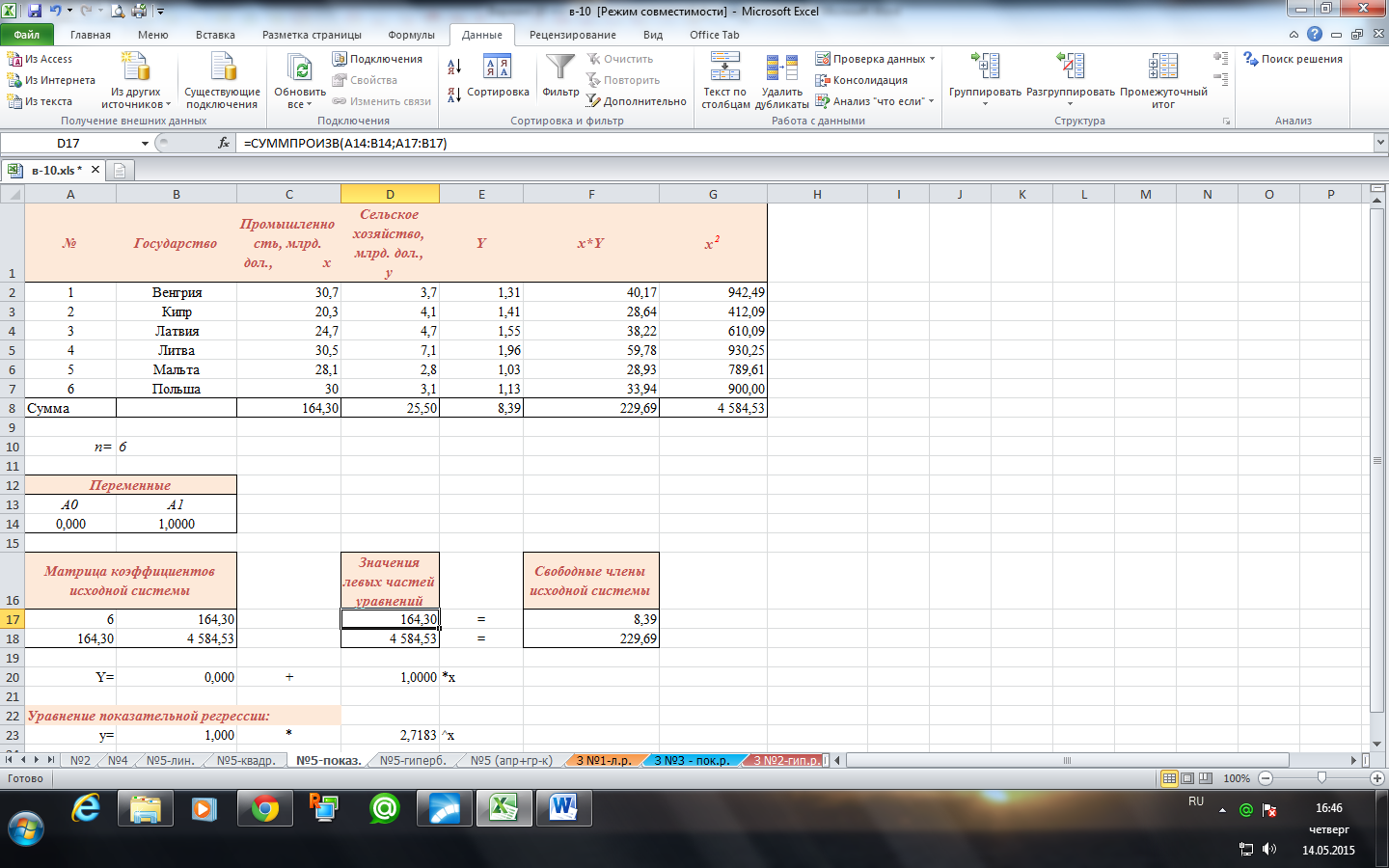
В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений 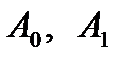 , во вторую строку записываем произвольные числовые значения 0 и 1.
, во вторую строку записываем произвольные числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных 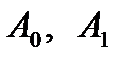 .
.
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных 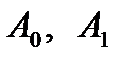 »; «диапазон первой строки матрицы коэффициентов исходной системы»).
»; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:
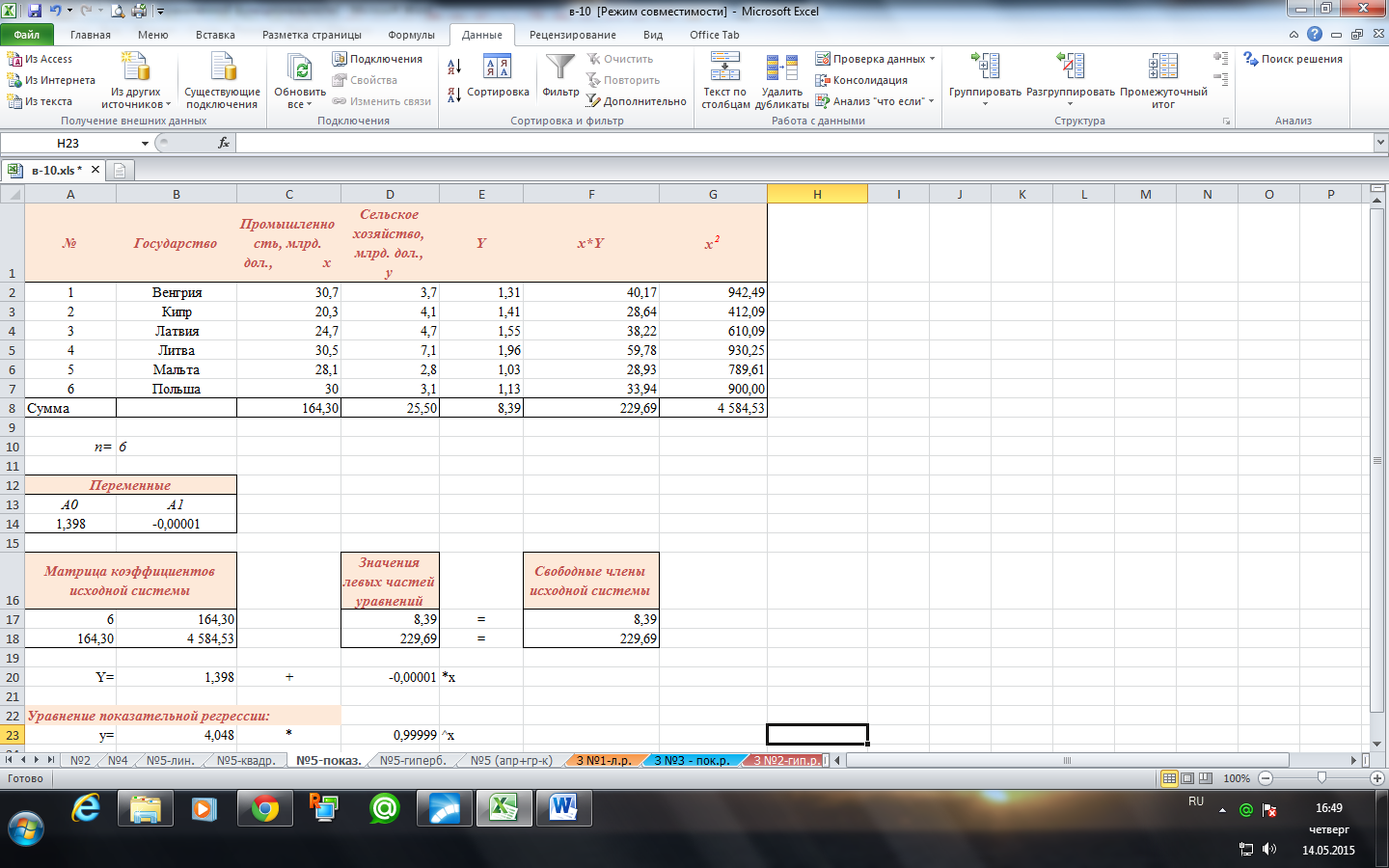
Уравнение регрессии в линейной форме будет иметь вид:
 .
.
Выполнив его потенцирование, вернемся к показательной регрессии:
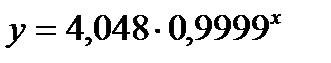 .
.
г) гиперболическая регрессия сводится к нахождению уравнения вида: 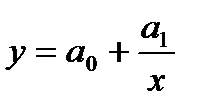
Для оценки параметров заменим  , тогда уравнение будет иметь вид:
, тогда уравнение будет иметь вид:
 .
.
Определим систему нормальных уравнений для нахождения оценок параметров полученной линейной регрессии.
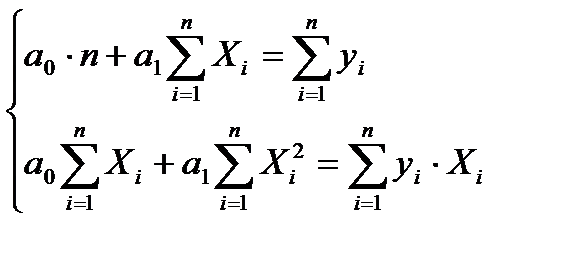
Для расчетов используем данные таблицы:
| № | Государство | Промышленность, млрд. дол., х | Сельское хозяйство, млрд. дол., y | Х | Х*y | X2 |
| Венгрия | 30,7 | 3,7 | 0,0326 | 0,12 | 0,001 | |
| Кипр | 20,3 | 4,1 | 0,0493 | 0,20 | 0,002 | |
| Латвия | 24,7 | 4,7 | 0,0405 | 0,19 | 0,002 | |
| Литва | 30,5 | 7,1 | 0,0328 | 0,23 | 0,001 | |
| Мальта | 28,1 | 2,8 | 0,0356 | 0,10 | 0,001 | |
| Польша | 3,1 | 0,0333 | 0,10 | 0,001 | ||
| Сумма | 164,30 | 25,50 | 0,22 | 0,95 | 0,009 |
Получим систему нормальных уравнений для линейной регрессии:
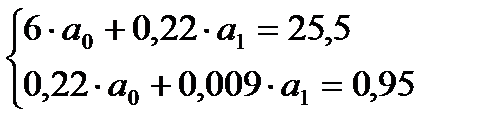
Решим данную систему, используя надстройку MS Excel Поиск решения.
Составим исходную табличную модель для решения системы линейных алгебраических уравнений.
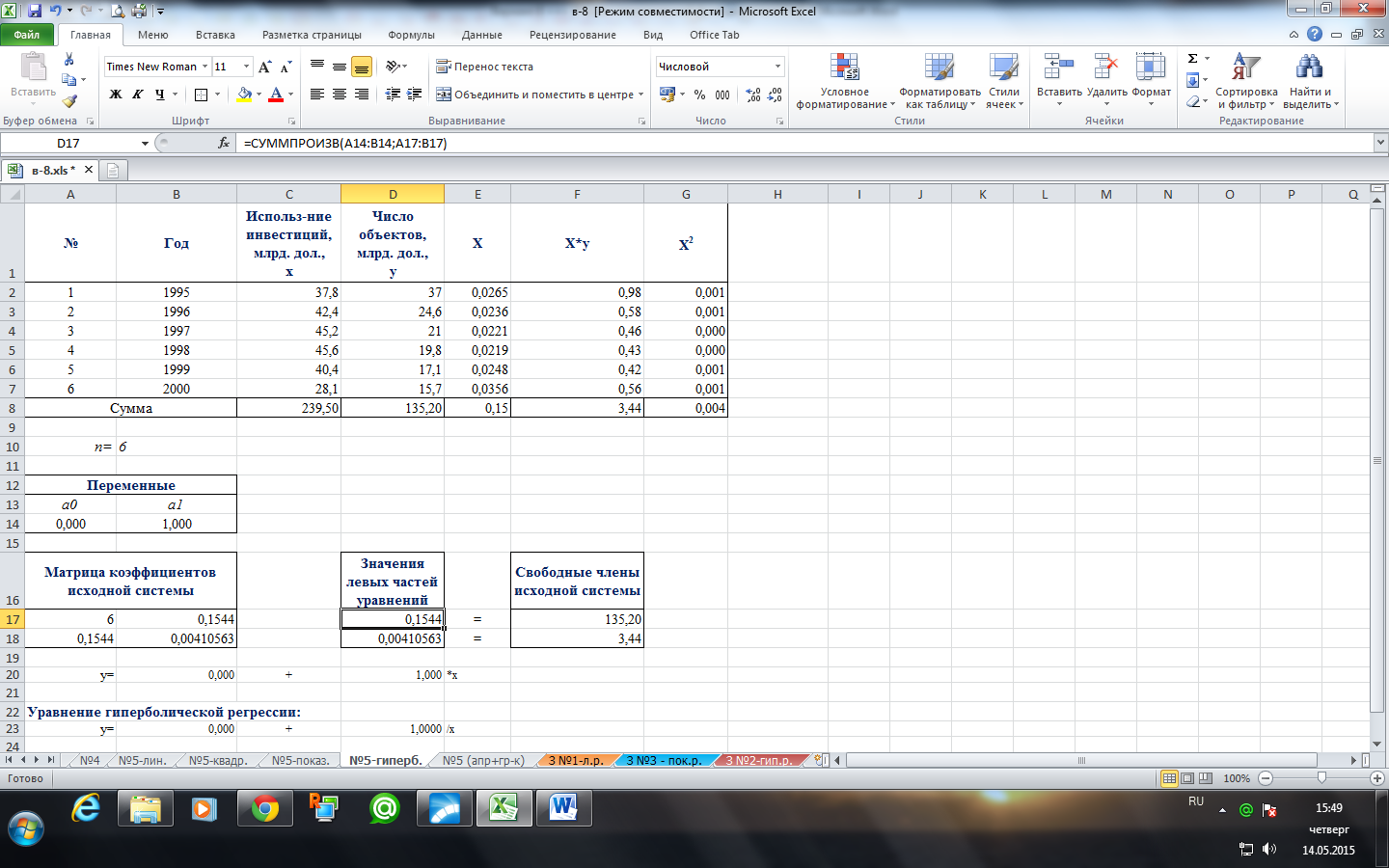
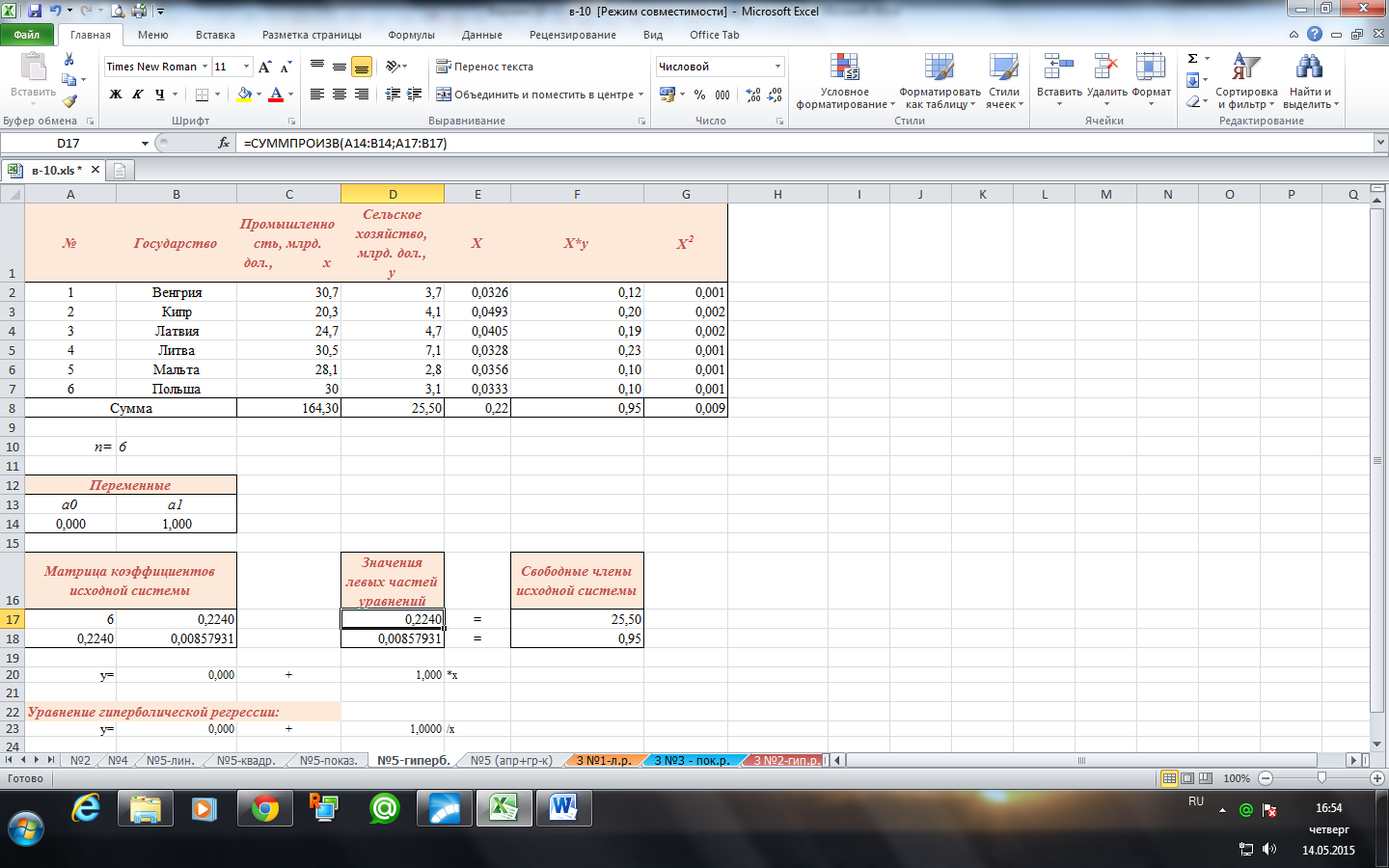
В блок «Переменные» в первую строку записываем переменные системы алгебраических уравнений 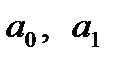 , во вторую строку записываем произвольные числовые значения 0 и 1.
, во вторую строку записываем произвольные числовые значения 0 и 1.
В блок «Матрица коэффициентов исходной системы» записываем соответствующую матрицу коэффициентов при переменных 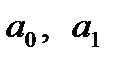 .
.
В блок «Значения левых частей уравнений» в верхнюю ячейку вводим формулу:
=СУММПРОИЗВ («фиксированный диапазон строки значений переменных  »; «диапазон первой строки матрицы коэффициентов исходной системы»).
»; «диапазон первой строки матрицы коэффициентов исходной системы»).
В блок «Свободные члены исходной системы» в столбец записываем значения правой части исходной системы.
Вызываем Поиск решения и заполняем форму:

Уравнение регрессии в линейной форме будет иметь вид:
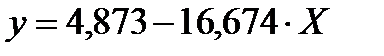 .
.
Вернемся к гиперболической регрессии:
 .
.
2. Найдем общую ошибку и среднюю ошибку аппроксимации, а затем укажем функцию лучшей аппроксимации.
Итак, получены следующие регрессии:
а) линейная - 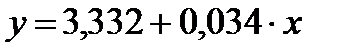 ,
,
б) квадратичная - 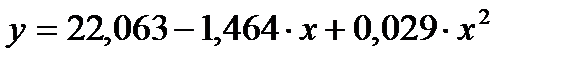 ,
,
в) показательная -  ,
,
г) гиперболическая -  .
.
Составим вспомогательную таблицу для расчетов необходимых значений.
| № | Государство | Промышленность, млрд. дол., х | Сельское хозяйство, млрд. дол., y | у-линейное | у-квадратич. | у-показат. | у- гипербол. | ||||||||||||||
| Венгрия | 30,7 | 3,7 | 4,3612 | 4,5944 | 4,0470 | 4,3294 | |||||||||||||||
| Кипр | 20,3 | 4,1 | 4,0125 | 4,3599 | 4,0472 | 4,0512 | |||||||||||||||
| Латвия | 24,7 | 4,7 | 4,1600 | 3,6898 | 4,0472 | 4,1975 | |||||||||||||||
| Литва | 30,5 | 7,1 | 4,3545 | 4,5305 | 4,0470 | 4,3259 | |||||||||||||||
| Мальта | 28,1 | 2,8 | 4,2740 | 3,9448 | 4,0471 | 4,2792 | |||||||||||||||
| Польша | 3,1 | 4,3377 | 4,3808 | 4,0470 | 4,3168 | ||||||||||||||||
| Сумма | 164,30 | 25,50 | 25,50 | 25,50 | 24,28 | 25,50 | |||||||||||||||
| № | Квадрат отклонения у-линейное | Квадрат отклонения у-квадратич. | Квадрат отклонения у-показат. | Квадрат отклонения у- гипербол. | Аппроксимация у-линейное | Аппроксимация у-квадратич. | Аппроксимация у-показат. | Аппроксимация у- гипербол. | |||||||||||||
| 0,4372 | 0,8000 | 0,1204 | 0,3962 | 0,1787 | 0,2417 | 0,0938 | 0,1701 | ||||||||||||||
| 0,0077 | 0,0675 | 0,0028 | 0,0024 | 0,0213 | 0,0634 | 0,0129 | 0,0119 | ||||||||||||||
| 0,2916 | 1,0206 | 0,4262 | 0,2525 | 0,1149 | 0,2149 | 0,1389 | 0,1069 | ||||||||||||||
| 7,5378 | 6,6026 | 9,3206 | 7,6957 | 0,3867 | 0,3619 | 0,4300 | 0,3907 | ||||||||||||||
| 2,1728 | 1,3105 | 1,5552 | 2,1880 | 0,5264 | 0,4089 | 0,4454 | 0,5283 | ||||||||||||||
| 1,5320 | 1,6403 | 0,8969 | 1,4805 | 0,3993 | 0,4131 | 0,3055 | 0,3925 | ||||||||||||||
| Сумма | 11,98 | 11,44 | 12,32 | 12,02 | 1,63 | 1,70 | 1,43 | 1,60 | |||||||||||||
| % | 27,1222% | 28,3994% | 23,7740% | 26,6741% | |||||||||||||||||
Введем в столбцы «у-линейное», «у-квадратичное», «у-показательное», «у-гиперболическое» полученные выше уравнения квадратичной, показательной и гиперболической регрессий соответственно и рассчитаем для них значения функций для каждого х.
Далее рассчитаем «Квадрат отклонения у-линейное», «Квадрат отклонения у-квадратичное», «Квадрат отклонения у-показательное» и «Квадрат отклонения у-гиперболическое» по соответствующим формулам для каждого х:
=СТЕПЕНЬ((«ячейка столбца y»-«ячейка столбца «у-линейное»);2)
=СТЕПЕНЬ((«ячейка столбца y»-«ячейка столбца «у-квадратичное»);2)
=СТЕПЕНЬ((«ячейка столбца y»-«ячейка столбца «у-показательное»);2)
=СТЕПЕНЬ((«ячейка столбца y»-«ячейка столбца «у-гиперболическое»);2)
Суммы значений этих столбцов и есть общие ошибки линейной, квадратичной, показательной и гиперболической регрессий соответственно.
На следующем этапе вычислим средние ошибки аппроксимации.
Для этого рассчитаем значения столбцов «Аппроксимация у-линейное», «Аппроксимация у-квадратичное», «Аппроксимация у-показательное», «Аппроксимация у-гиперболическое» по следующим формулам:
=ABS((«ячейка столбца y»-«ячейка столбца «у-линейное»)/«ячейка столбца y»)
=ABS((«ячейка столбца y»-«ячейка столбца «у-квадратичное»)/«ячейка столбца y»)
=ABS((«ячейка столбца y»-«ячейка столбца «у-показательное»)/«ячейка столбца y»)
=ABS((«ячейка столбца y»-«ячейка столбца «у-гиперболическое»)/«ячейка столбца y»)
Просуммируем значения всех столбцов с помощью функции СУММ, а результат суммирования запишем под столбцом с соответствующими данными.
В ячейках под столбцами «Аппроксимация у-линейное», «Аппроксимация у-квадратичное», «Аппроксимация у-показательное», «Аппроксимация у-гиперболическое» введем формулы и придадим этим ячейкам формат Процентный:
=1/6*СУММ(«диапазон значений ячеек соответствующего столбца»)*100%
Суммы значений этих столбцов – это средние ошибки аппроксимации линейной, квадратичной, показательной, гиперболической регрессий соответственно.
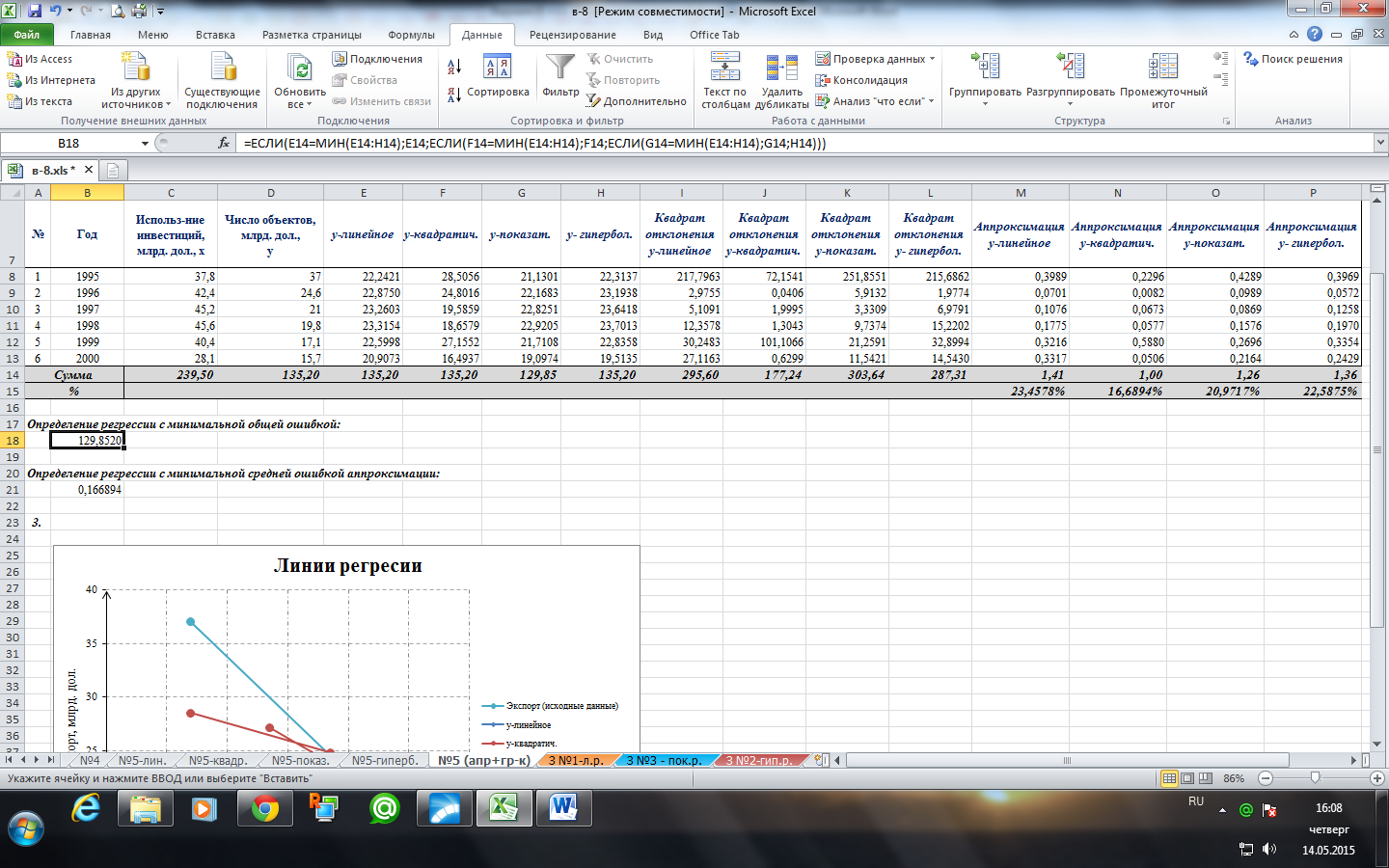
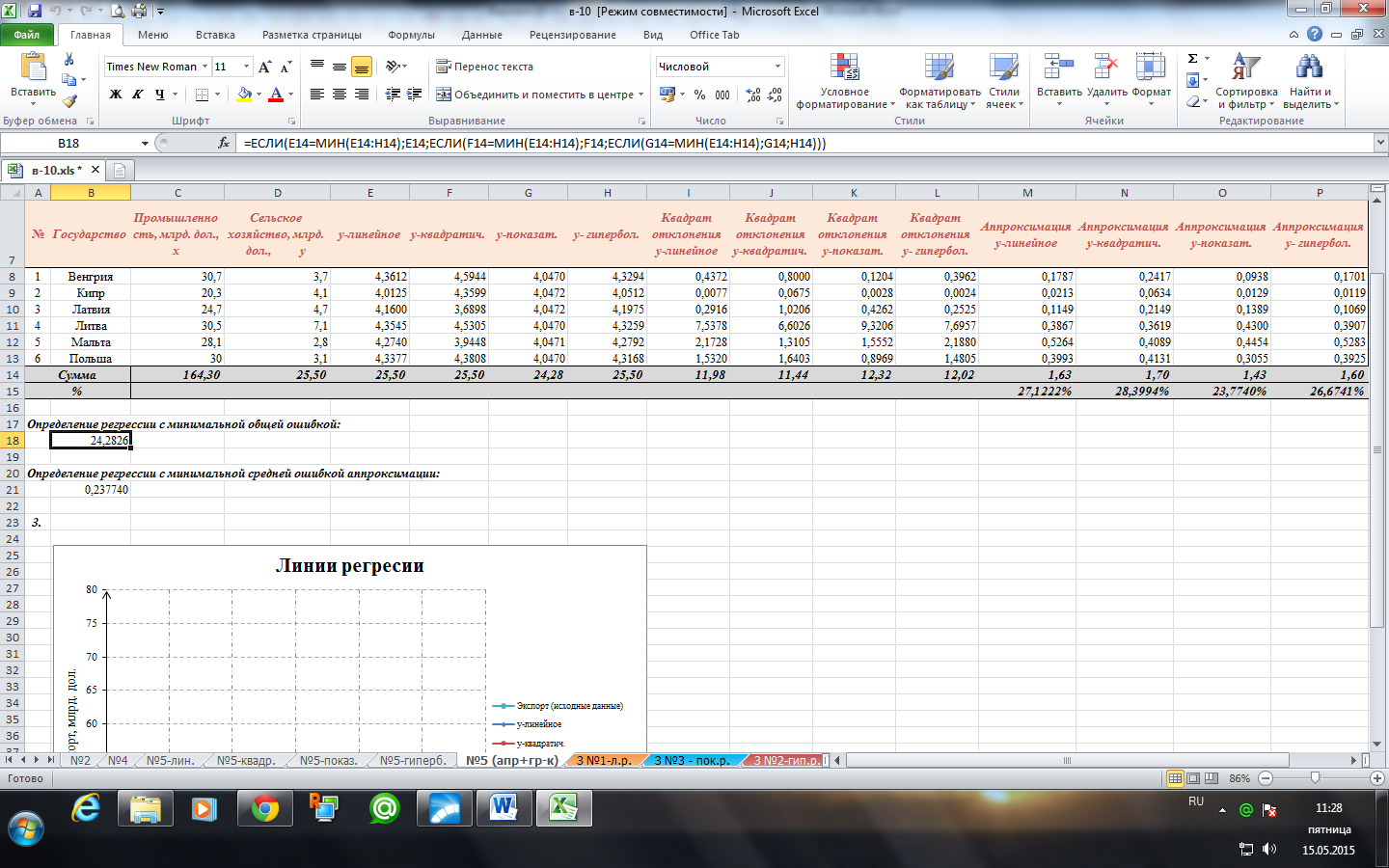
Таким образом, средние ошибки аппроксимации линейной, квадратичной, показательной, гиперболической регрессий соответственно равны 27,1222%, 28,3994%, 23,774%, 26,6741%.
Далее укажем функцию наилучшей аппроксимации по общей ошибке и по средней ошибке аппроксимации, используя функции ЕСЛИ и МИН.
Для определения регрессии с минимальной общей ошибкой введем формулу:
=ЕСЛИ(«ячейка суммы столбца «у-линейное»=МИН(«диапазон ячеек сумм регрессий»); «у-линейное»; ЕСЛИ(«ячейка суммы столбца «у-квадратичное»= МИН(«диапазон ячеек сумм регрессий»); «у-квадратичное»; ЕСЛИ(«ячейка суммы столбца «у-показательное»=МИН(«диапазон ячеек сумм регрессий»); «у-показательное»; «у-гиперболическое»)))
Для определения регрессии с минимальной средней ошибкой аппроксимации введем формулу:
=ЕСЛИ(«ячейка со значением средней ошибки аппроксимации «у-линейное»= МИН(«диапазон ячеек со значениями всех средних ошибок аппроксимации»); «у-линейное»; ЕСЛИ(«ячейка со значением средней ошибки аппроксимации «у-квадратичное»=МИН(«диапазон ячеек со значениями всех средних ошибок аппроксимации»); «у-квадратичное»; ЕСЛИ(«ячейка со значением средней ошибки аппроксимации «у-показательное»=МИН(«диапазон ячеек со значениями всех средних ошибок аппроксимации»); «у-показательное»; «у-гиперболическое»))).

Таким образом, минимальная общая ошибка и минимальная средняя ошибка аппроксимации у показательной функции.
Следовательно, показательная функция – функция наилучшей аппроксимации.
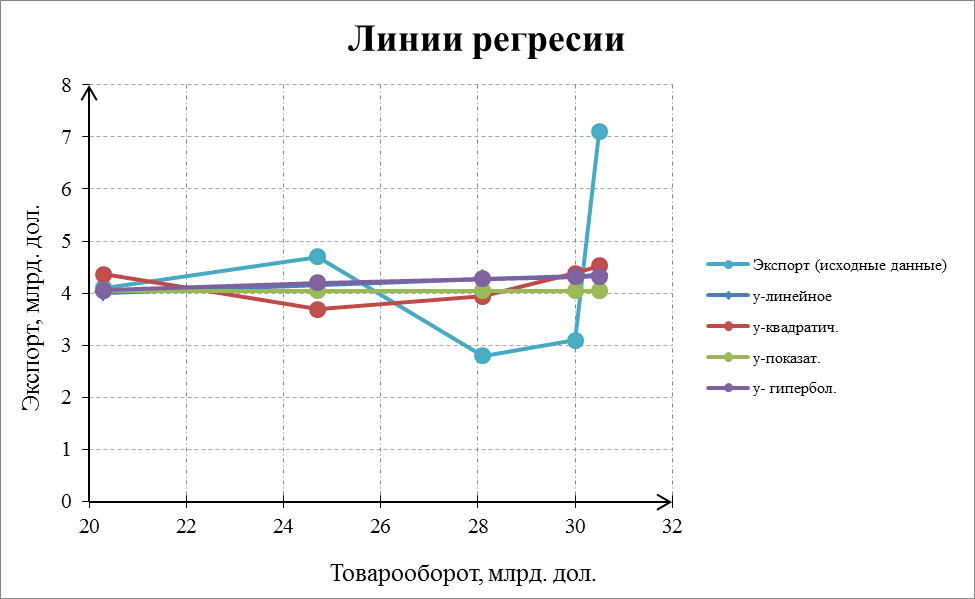
3. Построим полученные линии регрессии на одной плоскости вместе с исходными данными.
Заметим, что поскольку в предыдущей таблице значения аргумента функции не упорядочены по возрастанию, то мастер диаграмм не отразит правильно полученные регрессии. Для упорядочивания данных столбца необходимо отсортировать его по возрастанию, предварительно выделив все столбцы.
Date: 2015-09-25; view: 894; Нарушение авторских прав