Колебания, возникающие под действием внешних, периодически изменяющихся сил (при периодическом поступлении энергии извне к колебательной системе)

Ø Частота вынужденных колебаний равна частоте изменения внешней силы

Ø Если Fbc изменяется по закону синуса или косинуса, то вынужденные колебания будут гармоническими

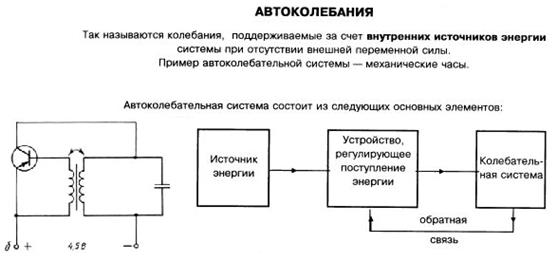
Ø При автоколебаниях необходимо периодическое поступлении энергии от собственного источника внутри колебательной системы

1. Гармонические колебания (уравнение, характеристика, график)

Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса

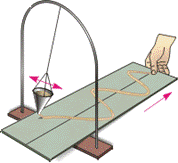
• уравнения гармонических колебаний (законы движения точек) имеют вид

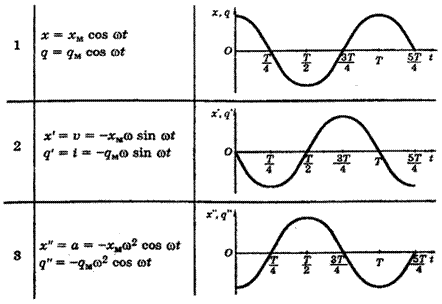
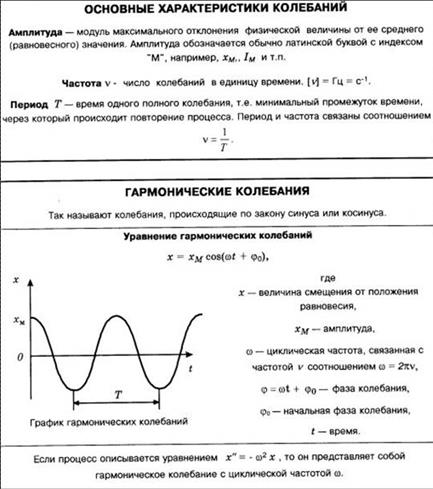
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.
Уравнение гармонических колебаний имеет вид:

,
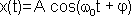где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); 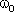- круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса 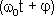- называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постояннаяφ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π/ .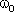
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота 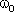= 2π/T = 2πν дает число колебаний за 2π секунд.

Обобщенное гармоническое колебание в дифференциальном виде

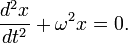
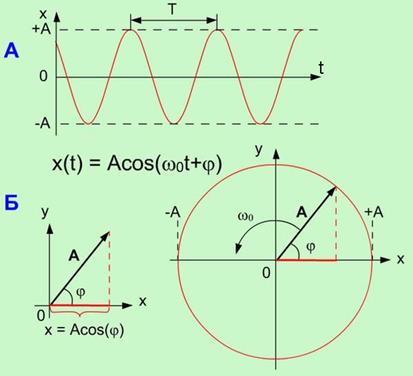
Графически гармонические колебания можно изображать в виде зависимости x от t (рис.1.1.А), так и методом вращающейся амплитуды (метод векторных диаграмм) (рис.1.1.Б).

Рисунок 1.1. Графическое изображение гармонических колебаний

Метод вращающейся амплитуды позволяет наглядно представить все параметры, входящие в уравнение гармонических колебаний. Действительно, если вектор амплитуды А расположен под углом φ к оси х (см. Рисунок 1.1. Б), то его проекция на ось х будет равна: x = Acos(φ). Угол φ и есть начальная фаза. Если вектор А привести во вращение с угловой скоростью 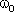, равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:
.
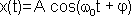Таким образом, длина вектора равна амплитуде гармонического колебания, направление вектора в начальный момент образует с осью x угол равный начальной фазе колебаний φ, а изменение угла направления от времени равно фазе гармонических колебаний. Время, за которое вектор амплитуды делает один полный оборот, равно периоду Т гармонических колебаний. Число оборотов вектора в секунду равно частоте колебаний ν.

1. Распространение колебаний в биологических средах. Поперечные и продольные волны

Если в каком-либо месте упругой среды (твердой, жидкой или газообразной) возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде от частицы к частице с некоторой скоростью v.

Например, если в жидкую или газообразную среду поместить колеблющееся тело, то колебательное движение тела будет передаваться прилегающим к нему частицам среды. Они, в свою очередь, вовлекают в колебательное движение соседние частицы и так далее. При этом все точки среды совершают колебания с одинаковой частотой, равной частоте колебания тела. Эта частота называется частотой волны.

Волной называется процесс распространения механических колебаний в упругой среде.

Частотой волны называется частота колебаний точек среды, в которой распространяется волна.

С волной связан перенос энергии колебаний от источника колебаний к периферийным участкам среды. При этом в среде возникают периодические деформации, которые переносятся волной из одной точки среды в другую. Сами частицы среды не перемещаются вместе с волной, а колеблются около своих положений равновесия. Поэтому распространение волны не сопровождается переносом вещества.

В соответствии с частотой механические волны делятся на различные диапазоны, которые указаны в табл. 2.1.

Таблица 2.1. Шкала механических волн

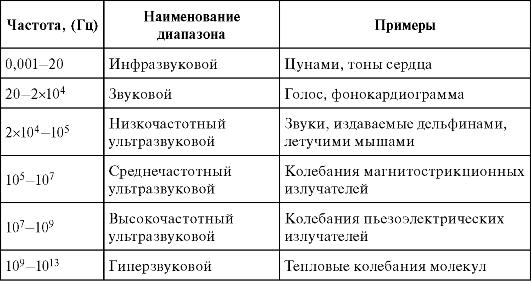В зависимости от направления колебаний частиц по отношению к направлению распространения волны, различают продольные и поперечные волны.

Продольные волны - волны, при распространении которых частицы среды колеблются вдоль той же прямой, по которой распространяется волна. При этом в среде чередуются области сжатия и разряжения.

Продольные механические волны могут возникать во всех средах (твердых, жидких и газообразных).

Поперечные волны - волны, при распространении которых частицы колеблются перпендикулярно направлению распространения волны. При этом в среде возникают периодические деформации сдвига.

В жидкостях и газах упругие силы возникают только при сжатии и не возникают при сдвиге, поэтому поперечные волны в этих средах не образуются. Исключение составляют волны на поверхности жидкости.

Date: 2015-09-24; view: 1332; Нарушение авторских прав