Перегрузка

При ускоренном движении тела и опоры с ускорением, направленным вертикально вверх, вес тела оказывается больше действующей на него силы тяжести.

В этом случае проекци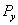и и 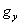положительны, а проекция 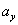отрицательна. Поэтому для модуля веса тела получаем выражение

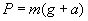. (8)

Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и на участке торможения космического корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при движении с большими ускорениями.

Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.

Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F_A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:

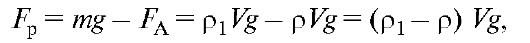
где ρ₁ - плотность вещества частицы; ρ - плотность воды; V - объем частицы.

Если значения ρ₁ и ρ мало отличаются друг от друга, то сила F_p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.

Рассмотрим физику этого явления.

Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO'. При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:

где ρ - плотность жидкости.

Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ₁(ρ₁ Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).

Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:

где m₁ - масса частицы, а ρ₁ - соответствующая ей плотность.

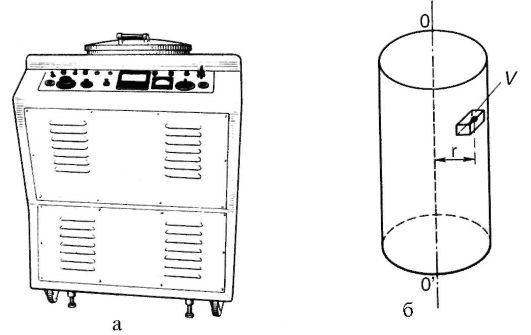
Рис. 5.21

Если F > F₁, то частица перемещается к оси вращения. Если F < F₁, то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F₁, которое обусловливает движение по окружности:

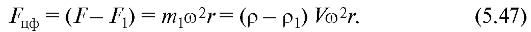
Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения¹.

Сравним разделение центрифугированием с разделением с помощью силы тяжести:

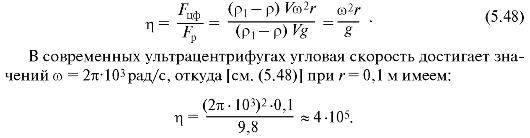
¹ Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.

Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.

Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.

1. Работа под действием переменной силы

Для характеристики действующей на тело силы F используется величина, называемая механической работой. Пусть под действием постоянной силыF тело переместилось из положения 1 в положение 2 (см. рис. 1). Перемещение характеризуется вектором S. Работой силы F на перемещении S называется скалярная величина, определяемая равенством: A = F · S ·cos. 1 Дж = 1 Н·м.

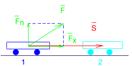
Свойства работы:

· Сила перпендикулярная перемещению работы не производит.

· Работа результирующей силы равна сумме работ составляющих сил.

· Работа на перемещении S равна сумме работ на отдельных участках этого перемещения.

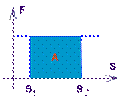Работу силы F при перемещении можно вычислить графически. Как следует из определения работы, ее значение равно площади закрашенного прямоугольника (см. рис. 2).

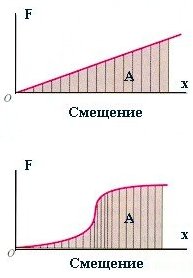Точно также определяется величина работы для

переменной силы, изменяющейся по более сложным

законам. На рис. 3 поясняется графический смысл

работы переменной силы F, направленной вдоль

осиOX.

Пример. Вычисление работы силы упругости

(см. рис. 4). A = F·x/2.

1. Импульс тела и закон сохранения импульса

Импульсом тела (материальной точки) называется ве­личина, равная произведению массы тела на его скорость.

Обозначив импульс (его также называют иногда количеством движения) буквой 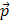, получим

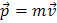. (2)

Из формулы (2) видно, что импульс — векторная ве­личина. Так как t > 0, то импульс имеет такое же на­правление, как и скорость (рис. 1).

Обозначим через 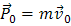импульс тела в начальный момент времени, а через 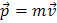— его импульс в конечный момент времени. Тогда 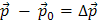есть изменение импульса тела за время ∆ t. Теперь уравнение (1) можно записать так:

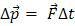(3)

Так как ∆ t > 0, то направления векторов 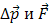совпадают. Соглас­но формуле (3) изменение импульса тела (материальной точки) про­порционально приложенной к нему силе и имеет такое же направление, как и сила.

Именно так был впервые сформу­лирован второй закон Ньютона.

Произведение силы на время ее действия называют импульсом силы. Поэтому можно сказать, что изменение импульса тела равно импуль­су действующей на него силы. Уравнение (3) пока­зывает, что одинаковые изменения импульса могут быть получены в результате действия большой силы в течение малого интервала времени или малой силы за большой промежуток времени.

Единица импульса не имеет особого названия, а ее наименование получается из определения этой величины (см. формулу (2)):

1 ед. импульса = 1 кг · 1 м/с = 1 кг · м/с.

Для нахождения импульса тела, которое нельзя счи­тать материальной точкой, поступают так: мысленно раз­бивают тело на отдельные малые элементы (материальные точки), находят импульсы полученных элементов, а потом суммируют их как векторы. Импульс тела равен сумме импульсов его отдельных элементов.

Импульс тела может быть равен нулю даже в том слу­чае, когда оно движется. Примером может служить вра­щающийся вокруг неподвижной оси однородный диск. Действительно, два диаметрально противоположных, рав­ных по массе элемента А и В имеют одинаковые по моду­лю скорости (рис. 5.2). Следовательно, их импульсы рав­ны по модулю, но противоположно направлены: 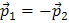, поэтому 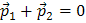. Такие равенства справедливы для любых двух диаметрально противоположных элементов диска.

Второй закон Ньютона может быть записан в импульс­ной форме: изменение импульса тела равно импульсу дей­ствующей на него силы.

Закон сохранения импульса является следствием вто­рого и третьего законов Ньютона.

Для простоты будем считать, что система состоит всего из двух тел. Это могут быть две звезды, два бильярдных шара или два других тела.

Силы, возникающие в результате взаимодействия тела, принадлежащего системе, с телом, не принадлежащим ей, называются внешними силами. Если рассматривать систему, состоящую из двух бильярдных шаров, то сила взаимодействия шаров с краем стола при ударе о него, сила трения шара о поверхность стола — внешние силы. Пусть на тела системы действуют внешние силы .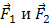

Силы, возникающие в результатевзаимодействия тел, принадлежащих системе, называются внутренними силами. Обозначим их через 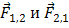(рис. 3). По третьему закону Ньютона 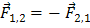.Отсюда следует, что сумма внутренних сил всегда равна нулю:

. (4)

Вследствие действия сил на тела системы их импульсы изменяются. Если взаимодействие рассматривается за ма­лый промежуток времени Δ t, то для тел системы можно записать второй закон Ньютона в виде

_-

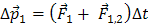
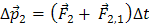Сложив эти равенства, получим

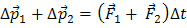. (5)

В левой части равенства (5) стоит сумма изменений импульсов всех тел системы, т. е. изменение импульса са­мой системы (под импульсом системы мы будем понимать геометрическую сумму импульсов всех тел системы):

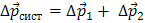. (6)

Учитывая равенство (5), можно равенство (6) запи­сать так:

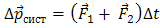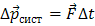, . (7)

где 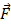— геометрическая сумма всех внешних сил, действу­ющих на тела системы.

Мы доказали весьма важное положение: импульс сис­темы тел могут изменить только внешние силы, причем изменение импульса системы 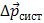совпадает по направ­лению с суммарной внешней силой. Внутренние силы из­меняют импульсы отдельных тел системы, но изменить суммарный импульс системы они не могут.

Уравнение (7) справедливо для любого интервала вре­мени Δ t, если сумма внешних сил остается постоянной.

Из уравнения (7) вытекает закон сохранения импуль­са. Если внешние силы на систему не действуют или их сумма равна нулю, то 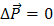и импульс системы остается неизменным, или, как говорят, сохраняется:

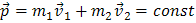. (8)

Закон сохранения импульса формулируется так: если сумма внешних сил равна нулю, то импульс системы тел сохраняется. Иначе говоря, в этом слу­чае тела могут только обмениваться импульсами, суммар­ное же значение импульса не изменяется.

Импульс, очевидно, сохраняется в изолированной сис­теме тел, так как в этой системе на тела вообще не дейст­вуют внешние силы. Но область применения закона сохра­нения импульса шире: если даже на тела системы действуют внешние силы, но их сумма равна нулю (т. е. система является замкнутой), то импульс системы все равно сохраняется.

Полученный результат справедлив для системы, содер­жащей произвольное число тел:

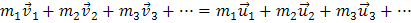, (9)

где 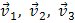, … — скорости тел в начальный момент времени; 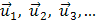— скорости тел в конечный момент.

Так как импульс — векторная величина, то уравне­ние (9) представляет собой компактную запись трех уравнений для проекций импульсов системы на оси коор­динат.

Если сумма внешних сил не равна нулю, но сумма про­екций сил на какое-то направление равна нулю, то проек­ция суммарного импульса системы на это направление не меняется. Например, систему тел на Земле или вблизи по­верхности Земли нельзя считать изолированной, так как на тела действует внешняя сила — сила тяжести. Однако вдоль горизонтального направления сила тяжести не дей­ствует и сумма проекций импульсов тел на это направле­ние будет оставаться неизменной, если действием сил тре­ния можно пренебречь.

В изолированной системе тел импульс системы сохра­няется. Также он может сохраняться в случае, если сумма внешних сил, действующих на систему, равна нулю.

1. Момент импульса и закон сохранения момента импульса

Date: 2015-09-24; view: 668; Нарушение авторских прав