Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Момент вращающейся силы приложенной к телу, равен произведению момента инерции тела на угловое ускорение
|
|
Моменты инерции тел правильной геометрической формы.
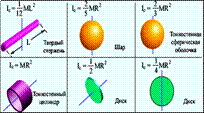
Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения. Но если масса считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения
Если для какого-либо тела известен его момент инерции относительно оси, проходящей через центр тяжести, то легко может быть найден и момент инерции относительно любой оси, параллельной первой
Теорема Штейнера
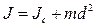, где
Jc – момент инерции относительно оси, проходящей через центр тяжести
m – масса диска
d – расстояние между осями
Т.Шнайдера: Момент инерции относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр тяжести, сложенному с произведением массы тела на квадрат расстояния от центра тяжести тела до оси вращения
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси
Пусть твердое тело вращается вокруг неподвижной оси О–О¢. Разобьем это тело на элементарные участки mi. Выбираем произвольную материальную точку, принадлежащую этому телу. Точка вместе с вращающимся телом описывает окружность. Проведем от точки линию и обозначим ее Ri. Приложим к точке силу Fi
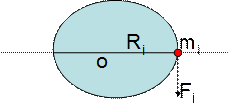
Под действием силы `Fi, направленной перпендикулярно к оси по касательной к окружности, описываемой материальной точкой, движущаяся точка начнет вращательное движение. По второму закону Ньютона
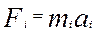
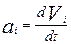
Используем формулу, устанавливающую связь между линейной и угловой скоростью
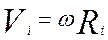
где w – угловая скорость; у всех точек вращающегося тела она одинакова
Подставим значение линейной скорости в формулу ускорения
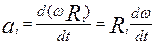
Подставим значение ускорения во второй закон Ньютона
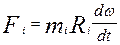
умножим обе части последнего равенства на Ri и просуммируем его
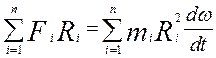
где:
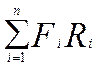- момент силы
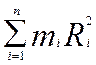-момент инерции
-угловое ускорение
Основное уравнение динамики вращательного движения или второй закон Ньютона для вращательного движения
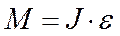
Момент вращающейся силы приложенной к телу, равен произведению момента инерции тела на угловое ускорение
Date: 2015-09-24; view: 730; Нарушение авторских прав