
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Практический блок. Задание 1: Изучить теоретический материал и составить конспект темы по вопросам:
|
|
Теоретический блок
Задание 1: Изучить теоретический материал и составить конспект темы по вопросам:
1) Двугранный угол и его измерение.
2) Перпендикулярные плоскости. Признак перпендикулярности плоскостей.
3) Параллельная и ортогональная проекции, свойства.
4) Многогранники. Правильные многогранники.
Методические указания
Перед выполнением теоретического блока следует внимательно изучить задания, подобрать необходимый материал, воспользоваться списком рекомендованной литературы. При необходимости нужно использовать справочники и другие доступные источники информации. Обязательно необходимо указать все данные источника (автор, название, год выпуска, издательство, название сайта, электронный адрес).
Отчёт по теоретическому блоку работы следует оформлять придерживаясь следующего последовательности: основные понятия, определения, рисунки, схемы, формулы, теоремы (желательно с доказательством) и следующего содержания: введение, основная часть, примеры с решениями (объяснениями), заключение, список используемой литературы. Титульный лист выполненного задания по теоретическому блоку следует напечатать по образцу (Приложение № 1).
Рекомендуемая литература:
1. Богомолов Н.В.,Самойленко П.И. Математика. –М.:Дрофа,2009.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
6. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
7. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
8. INTERNET
Теоретический блок является основой для выполнения практического блока.
Практический блок
Задание 2: Решить следующие задачи:
Задача № 1: Через вершину В ромба ABCD, проведена прямая BM 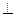 его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ=750 см.,
его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ=750 см., 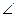 АВС=120˚, ВМ=375 см.
АВС=120˚, ВМ=375 см.
Задача №2: Найти площадь сечения, проведенного через середины двух смежных боковых ребер правильной 4 – угольной пирамиды со стороной основания 20дм., и высотой 16дм. 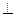 основанию пирамиды.
основанию пирамиды.
Задача № 3: Стороны оснований правильной треугольной усеченной пирамиды 18 м. и 30м. Боковая грань образует с меньшим основанием 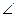 135˚. Найти высоту усеченной
135˚. Найти высоту усеченной
Задача № 4: Стороны оснований правильной усеченной 4- угольной пирамиды 6м и 14 м. апофема = 5м. Найти высоту пирамиды, полную поверхность, боковое ребро, площадь диагонального сечения.
Методические указания
Для выполнения данного задания внимательно изучите приведенные ниже примеры с подробными решениями, а затем выполните аналогичные практические задания.
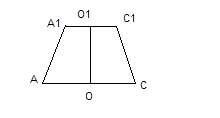
Пример 1: Стороны оснований правильной усеченной 4- угольной пирамиды = 6м и 14 м. Апофема = 5м. Найти высоту пирамиды, полную поверхность, боковое ребро, площадь диагонального сечения.
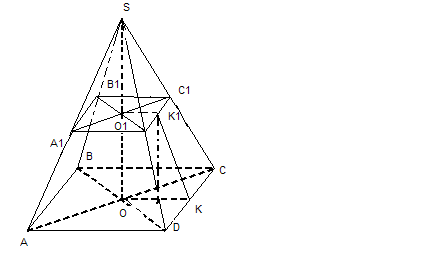
Дано: (A-D 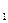 )- правильная усеченная пирамида; K
)- правильная усеченная пирамида; K 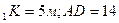 м, A
м, A 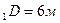
Найти: О  ; S
; S  ; S
; S 
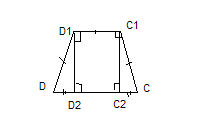
Решение: 1)
ΔD  по т. Пифагора: D
по т. Пифагора: D 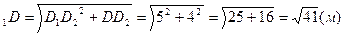
2)S 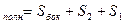
3)S 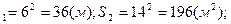
S 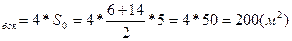
4)S 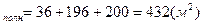
5) 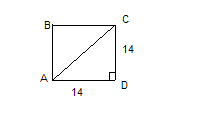 AC=
AC= 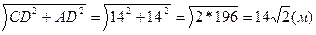
Аналогично найдем A 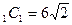
6)  S
S 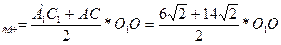
7) 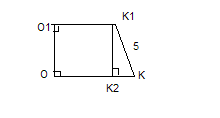 K
K 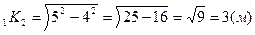
8)S 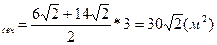 Ответ: O
Ответ: O 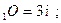 S
S 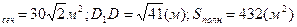
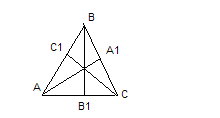
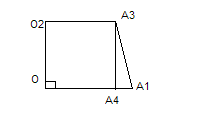
Пример 2: Стороны оснований правильной треугольной усеченной пирамиды 6 м. и 10 м. Боковая грань образует с меньшим основанием 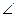 120˚. Найти высоту усеченной пирамиды.
120˚. Найти высоту усеченной пирамиды.
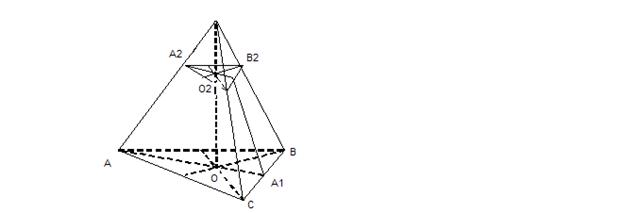
Дано: (A-C 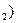 - правильная усеченная пирамида.
- правильная усеченная пирамида.
АС=10м, А 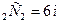 ,
, 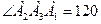
Найти: ОО 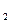 Решение:
Решение:
1)  tg30=
tg30= 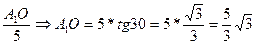 аналогично A
аналогично A 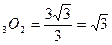
2)  A
A 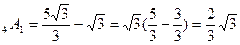
3)tg30=  Ответ:
Ответ: 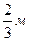
Пример3: Через вершину б ромба ABCD, проведена прямая BM  его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ=25 см.,
его плоскости. Найти расстояние от точки М до прямых, содержащих стороны ромба, если АВ=25 см.,  ВАD=60˚, ВМ=12,5 см.
ВАD=60˚, ВМ=12,5 см.
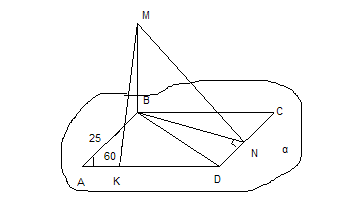
Дано: ABCD – ромб; AB=25см.; BM  ; BM=12,5см,
; BM=12,5см,  ˚
˚
Найти: MN
Решение:
1) 
MB 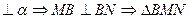
MN= 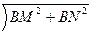 , BN-?
, BN-?
2)ΔBCN(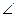 N=90˚)
N=90˚)
BN= 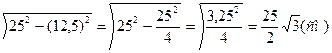
3)MN= 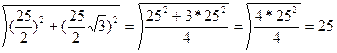
Пример4: Найти площадь сечения, проведенного через середины двух смежных боковых ребер правильной 4 – угольной пирамиды со стороной основания а, и высотой H 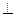 основанию пирамиды.
основанию пирамиды.
Дано: SABCD - правильная пирамида; SC=15см, AC=24см; SC  ;SD
;SD 
K 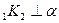 .
.
Найти: S 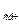
Решение:
1)ΔOSC 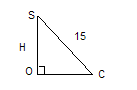
SO= 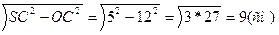
2)
 sin45=
sin45= 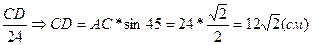
3)
 D
D 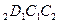 - равнобед. трапеция.
- равнобед. трапеция.
S 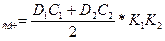 , K
, K 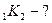
D 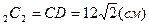 D
D 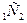 -?
-?
4)  D
D  - линия основания.
- линия основания.
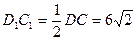 (см)
(см)
5)
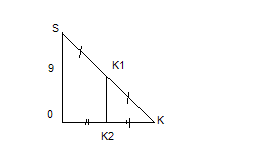
K 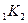 - средняя линия Δ OSK
- средняя линия Δ OSK
K 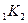 =
= 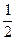 OS=4,5(см)
OS=4,5(см)
6)S 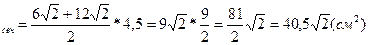
Ответ: 40,5 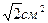
Рекомендуемая литература:
1. Богомолов Н.В.,Самойленко П.И. Математика. –М.:Дрофа,2009.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие, 10-е изд. – М.: Высшая школа, 2008.
3. Валуцэ И.И. Математика для техникумов. - М.: Наука,2008.
4. Выгодский М.Я. Справочник по высшей математике. – М.: Рост книга, 2009.
5. С.Г. Григорьев, С.В.Задулина. Математика.-М.: АСАDEMA,2008.
6. Дадаян А.А. Сборник задач по математике.-М.: ФОРУМ-ИНФРА-М,2009.
7. Дадаян А.А. Математика.-М.: ФОРУМ-ИНФРА-М,2009.
8. INTERNET
Форма отчетности
Выполненные задания оформить по одному из трёх вариантов:
1) Напечатать в программе MICROSOFT WORD (кегль - 14, интервал – 1,5; шрифт - Times New Roman; поля – 1,2,1,1; нумерация страниц). Сохранить файл под своей фамилией и сдать электронную версию преподавателю на носителе. Распечатать на листах формата А4.
2) Письменно на листах формата А4, с одной стороны, ручкой синего или чёрного цвета.
3) Обычный текст распечатать на листах формата А4, а математический текст и рисунки письменно от руки также на листах А4.
Во всех трех вариантах оформить титульный лист (Приложение 1), работу вложить в файл и сдать в назначенный срок.
Критерии оценивания работы:
Каждое выполненное задание теоретического и практического блоков самостоятельной работы оценивается в баллах по 5-бальной системе. Учитывается полнота выполнения и объём, грамотность, научность, последовательность и аккуратность оформления. Затем выставляется общая (усреднённая) оценка за всю работу в целом.
Максимальное количество баллов по данной работе 10. Итоговая оценка за работу: «5»- 10 баллов, «4» - (7-9) баллов, «3» - (5-6) баллов.
Оценка выставляется в журнал для учёта самостоятельных работ. Каждая работа должна быть сдана в строго установленные строки, в противном случае преподаватель имеет право снизить оценку, а при её невыполнении поставить неудовлетворительную оценку.
Date: 2015-09-24; view: 443; Нарушение авторских прав