
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание № 5
|
|
Исследуется зависимость месячного расхода семьи на продукты питания zi, тыс.р. от месячного дохода на одного человека семьи хi, тыс.р., от размера семьи уi, чел. и от количества детей в семье ui, чел. Необходимо:
1.В соответствии с методом наименьших квадратов найти уравнение множественной линейной регрессии 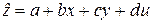 .
.
Найти парные коэффициенты корреляции rxy, rxz, ryz, rxu, ryu, rzu.
2.С доверительной вероятностью 0,95 проверить коэффициенты корреляции на значимость.
3.Вычислить индекс множественной корреляции и проверить с доверительной вероятностью 0,95 его статистическую значимость.
| Значения факторов хi и уi (одинаковое для всех вариантов). | |||||||||||||||
| хi | |||||||||||||||
| уi | |||||||||||||||
| ui | |||||||||||||||
| Вар. | Значение фактора zi (по вариантам). | ||||||||||||||
| 2,3 | 2,1 | 2,9 | 2,7 | 3,2 | 3,4 | 3,8 | 4,2 | 4,2 | 4,5 | 5,2 | 5,8 | 4,7 | 5,5 | 5,1 |
| хi | уi | ui | Zi |
| 2,3 | |||
| 2,1 | |||
| 2,9 | |||
| 2,7 | |||
| 3,2 | |||
| 3,4 | |||
| 3,8 | |||
| 4,2 | |||
| 4,2 | |||
| 4,5 | |||
| 5,2 | |||
| 5,8 | |||
| 4,7 | |||
| 5,5 | |||
| 5,1 |
РЕШЕНИЕ
Переобозначим
Xi=x1
Yi=x2
Ui=x3
Zi=y
| Х1 | X2 | X3 | y |
| 2,3 | |||
| 2,1 | |||
| 2,9 | |||
| 2,7 | |||
| 3,2 | |||
| 3,4 | |||
| 3,8 | |||
| 4,2 | |||
| 4,2 | |||
| 4,5 | |||
| 5,2 | |||
| 5,8 | |||
| 4,7 | |||
| 5,5 | |||
| 5,1 |
Уравнение множественной регрессии может быть представлено в виде:
Y = f(β, X) + ε
где X = X(X1, X2,..., Xm) - вектор независимых (объясняющих) переменных; β - вектор параметров (подлежащих определению); ε - случайная ошибка (отклонение); Y - зависимая (объясняемая) переменная.
теоретическое линейное уравнение множественной регрессии имеет вид:
Y = β0 + β1X1 + β2X2 +... + βmXm + ε
β0 - свободный член, определяющий значение Y, в случае, когда все объясняющие переменные Xj равны 0.
Прежде чем перейти к определению нахождения оценок коэффициентов регрессии, необходимо проверить ряд предпосылок МНК.
Предпосылки МНК.
1. Математическое ожидание случайного отклонения εi равно 0 для всех наблюдений (M(εi) = 0).
2. Гомоскедастичность (постоянство дисперсий отклонений). Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = S2 для любых i и j.
3. отсутствие автокорреляции.
4. Случайное отклонение должно быть независимо от объясняющих переменных: Yeixi = 0.
5. Модель является линейное относительно параметров.
6. отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.
7. Ошибки εi имеют нормальное распределение. Выполнимость данной предпосылки важна для проверки статистических гипотез и построения доверительных интервалов.
Эмпирическое уравнение множественной регрессии представим в виде:
Y = b0 + b1X1 + b1X1 +... + bmXm + e
Здесь b0, b1,..., bm - оценки теоретических значений β0, β1, β2,..., βm коэффициентов регрессии (эмпирические коэффициенты регрессии); e - оценка отклонения ε.
При выполнении предпосылок МНК относительно ошибок εi, оценки b0, b1,..., bm параметров β0, β1, β2,..., βm множественной линейной регрессии по МНК являются несмещенными, эффективными и состоятельными (т.е. BLUE-оценками).
Для оценки параметров уравнения множественной регрессии применяют МНК.
1. Оценка уравнения регрессии.
Определим вектор оценок коэффициентов регрессии. Согласно методу наименьших квадратов, вектор s получается из выражения: s = (XTX)-1XTY
К матрице с переменными Xj добавляем единичный столбец:
Матрица Y
| 2.3 |
| 2.1 |
| 2.9 |
| 2.7 |
| 3.2 |
| 3.4 |
| 3.8 |
| 4.2 |
| 4.2 |
| 4.5 |
| 5.2 |
| 5.8 |
| 4.7 |
| 5.5 |
| 5.1 |
Матрица XT
Умножаем матрицы, (XTX)
В матрице, (XTX) число 15, лежащее на пересечении 1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки матрицы XT и 1-го столбца матрицы X
Умножаем матрицы, (XTY)
| 59.6 |
| 209.9 |
| 86.3 |
Находим обратную матрицу (XTX)-1
| 3.283 | -0.804 | -0.582 | 1.055 |
| -0.804 | 0.224 | 0.124 | -0.275 |
| -0.582 | 0.124 | 0.151 | -0.243 |
| 1.055 | -0.275 | -0.243 | 0.508 |
Вектор оценок коэффициентов регрессии равен
Уравнение регрессии (оценка уравнения регрессии)
Y = 0.8 + 0.32X1 + 0.65X2 + 0.11X3
2. Матрица парных коэффициентов корреляции R.
Число наблюдений n = 15. Число независимых переменных в модели равно 3, а число регрессоров с учетом единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y, размерность матрицы становится равным 5. Матрица, независимых переменных Х имеет размерность (15 х 5).
Матрица, составленная из Y и X
| 2.3 | ||||
| 2.1 | ||||
| 2.9 | ||||
| 2.7 | ||||
| 3.2 | ||||
| 3.4 | ||||
| 3.8 | ||||
| 4.2 | ||||
| 4.2 | ||||
| 4.5 | ||||
| 5.2 | ||||
| 5.8 | ||||
| 4.7 | ||||
| 5.5 | ||||
| 5.1 |
Транспонированная матрица.
| 2.3 | 2.1 | 2.9 | 2.7 | 3.2 | 3.4 | 3.8 | 4.2 | 4.2 | 4.5 | 5.2 | 5.8 | 4.7 | 5.5 | 5.1 |
Матрица ATA.
| 59.6 | ||||
| 59.6 | 256.2 | 209.9 | 86.3 | |
| 209.9 | ||||
| 86.3 |
Полученная матрица имеет следующее соответствие:
| ∑n | ∑y | ∑x1 | ∑x2 | ∑x3 |
| ∑y | ∑y2 | ∑x1 y | ∑x2 y | ∑x3 y |
| ∑x1 | ∑yx1 | ∑x1 2 | ∑x2 x1 | ∑x3 x1 |
| ∑x2 | ∑yx2 | ∑x1 x2 | ∑x2 2 | ∑x3 x2 |
| ∑x3 | ∑yx3 | ∑x1 x3 | ∑x2 x3 | ∑x3 2 |
Найдем парные коэффициенты корреляции.
| Признаки x и y | ∑xi | ∑yi | ∑xiyi | |||
| Для y и x1 | 3.4 | 59.6 | 3.973 | 209.9 | 13.993 | |
| Для y и x2 | 59.6 | 3.973 | 13.4 | |||
| Для y и x3 | 1.2 | 59.6 | 3.973 | 86.3 | 5.753 | |
| Для x1 и x2 | 3.4 | 10.4 | ||||
| Для x1 и x3 | 1.2 | 3.4 | 4.667 | |||
| Для x2 и x3 | 1.2 | 4.667 |
| Признаки x и y | ||||
| Для y и x1 | 0.907 | 1.293 | 0.952 | 1.137 |
| Для y и x2 | 1.293 | 1.414 | 1.137 | |
| Для y и x3 | 0.96 | 1.293 | 0.98 | 1.137 |
| Для x1 и x2 | 0.907 | 1.414 | 0.952 | |
| Для x1 и x3 | 0.96 | 0.907 | 0.98 | 0.952 |
| Для x2 и x3 | 0.96 | 0.98 | 1.414 |
Матрица парных коэффициентов корреляции R:
| - | y | x1 | x2 | x3 |
| y | 0.447 | 0.92 | 0.885 | |
| x1 | 0.447 | 0.149 | 0.629 | |
| x2 | 0.92 | 0.149 | 0.77 | |
| x3 | 0.885 | 0.629 | 0.77 |
Коллинеарность – зависимость между факторами. В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:
r(xjy) > r(xkxj); r(xky) > r(xkxj).
Если одно из неравенств не соблюдается, то исключается тот параметр xk или xj, связь которого с результативным показателем Y оказывается наименее тесной.
Для отбора наиболее значимых факторов xi учитываются следующие условия:
- связь между результативным признаком и факторным должна быть выше межфакторной связи;
- связь между факторами должна быть не более 0.7. Если в матрице есть межфакторный коэффициент корреляции rxjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.;
- при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. В этом случае среди столбцов матрицы факторных переменных Х имеются линейно зависимые столбцы, и, по свойству определителей матрицы, det(XTX = 0).
Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Если между факторными переменными имеется высокая степень корреляции, то матрица (XTX) близка к вырожденной, т. е. det(XTX ≧ 0) (чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии).
Вычисление определителя показано в шаблоне решения Excel
В нашем случае rx2 x3 имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.
Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых |ryxi| < 0.5 исключают из модели. Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции (по шкале Чеддока): если |r|>0.3 – связь практически отсутствует; 0.3 ≤ |r| ≤ 0.7 - связь средняя; 0.7 ≤ |r| ≤ 0.9 – связь сильная; |r| > 0.9 – связь весьма сильная.
Проверим значимость полученных парных коэффициентов корреляции с помощью t-критерия Стьюдента. Коэффициенты, для которых значения t-статистики по модулю больше найденного критического значения, считаются значимыми.
Рассчитаем наблюдаемые значения t-статистики для ryx1 по формуле:
где m = 1 - количество факторов в уравнении регрессии.
По таблице Стьюдента находим Tтабл
tкрит(n-m-1;α/2) = (13;0.025) = 2.16
Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - не значим
Рассчитаем наблюдаемые значения t-статистики для ryx2 по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Рассчитаем наблюдаемые значения t-статистики для ryx3 по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Таким образом, связь между (y и xx2 ), (y и xx3 ) является существенной.
Наибольшее влияние на результативный признак оказывает фактор x2 (r = 0.92), значит, при построении модели он войдет в регрессионное уравнение первым.
Тестирование и устранение мультиколлинеарности.
Наиболее полным алгоритмом исследования мультиколлинеарности является алгоритм Фаррара-Глобера. С его помощью тестируют три вида мультиколлинеарности:
1. Всех факторов (χ2 - хи-квадрат).
2. Каждого фактора с остальными (критерий Фишера).
3. Каждой пары факторов (критерий Стьюдента).
1. Проверим переменные на мультиколлинеарность методом Фаррара-Глоубера по первому виду статистических критериев (критерий "хи-квадрат").
Формула для расчета значения статистики Фаррара-Глоубера:
χ2 = -[n-1-(2m+5)/6]ln(det[R]) = -[15-1-(2*3+5)/6]ln(0.00709) = 60.21
где m = 3 - количество факторов, n = 15 - количество наблюдений, det[R] - определитель матрицы парных коэффициентов корреляции R.
Сравниваем его с табличным значением при v = m/2(m-1) = 3 степенях свободы и уровне значимости α. Если χ2 > χтабл2, то в векторе факторов присутствует мультиколлинеарность.
χтабл2(3;0.05) = 7.81473
2. Проверим переменные на мультиколлинеарность по второму виду статистических критериев (критерий Фишера).
Определяем обратную матрицу D = R-1:
| 18.848 | -5.064 | -15.254 | -1.745 |
| -5.064 | 4.407 | 6.607 | -3.379 |
| -15.254 | 6.607 | 16.866 | -3.646 |
| -1.745 | -3.379 | -3.646 | 7.475 |
Вычисляем F-критерии Фишера:
где dkk - диагональные элементы матрицы.
Рассчитанные значения критериев сравниваются с табличными при v1=n-m и v2=m-1 степенях свободы и уровне значимости α. Если Fk > FТабл, то k-я переменная мультиколлинеарна с другими.
v1=15-3 = 12; v2=3-1 = 2. FТабл(12;2) = 19.4
Поскольку F1 > Fтабл, то переменная y мультиколлинеарна с другими.
Поскольку F2 > Fтабл, то переменная x1 мультиколлинеарна с другими.
Поскольку F3 > Fтабл, то переменная x2 мультиколлинеарна с другими.
Поскольку F4 > Fтабл, то переменная x3 мультиколлинеарна с другими.
3. Проверим переменные на мультиколлинеарность по третьему виду статистических критериев (критерий Стьюдента). Для этого найдем частные коэффициенты корреляции.
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и xi) при условии, что влияние на них остальных факторов (xj) устранено.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx1 /x2 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
где k = 1 - число фиксируемых факторов.
По таблице Стьюдента находим Tтабл
tкрит(n-k-2;α/2) = (12;0.025) = 2.179
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x1 при условии, что x2 войдет в модель, стала сильнее.
Теснота связи не сильная
Определим значимость коэффициента корреляции ryx1 /x3 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
где k = 1 - число фиксируемых факторов.
По таблице Стьюдента находим Tтабл
tкрит(n-k-2;α/2) = (12;0.025) = 2.179
Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - не значим
Как видим, связь y и x1 при условии, что x3 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x1 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx2 /x1 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x2 при условии, что x1 войдет в модель, стала сильнее.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx2 /x3 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x2 при условии, что x3 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x2 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx3 /x1 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x3 при условии, что x1 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx3 /x2 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x3 при условии, что x2 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx2 /y.
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x2 при условии, что y войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x2 остается нецелесообразным.
Теснота связи умеренная
Определим значимость коэффициента корреляции ryx2 /x3 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x2 при условии, что x3 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x2 остается нецелесообразным.
Теснота связи умеренная
Определим значимость коэффициента корреляции ryx3 /y.
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x3 при условии, что y войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx3 /x2 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x3 при условии, что x2 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Теснота связи низкая. Межфакторная связь слабая.
Определим значимость коэффициента корреляции ryx3 /y.
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл < tкрит, то принимаем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - не значим
Как видим, связь y и x3 при условии, что y войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Теснота связи сильная
Определим значимость коэффициента корреляции ryx3 /x1 .
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим
Как видим, связь y и x3 при условии, что x1 войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x3 остается нецелесообразным.
Можно сделать вывод, что при построении регрессионного уравнения следует отобрать факторы x2, x3.
Модель регрессии в стандартном масштабе.
Модель регрессии в стандартном масштабе предполагает, что все значения исследуемых признаков переводятся в стандарты (стандартизованные значения) по формулам:
где хji - значение переменной хji в i-ом наблюдении.
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квадратическое отклонение S.
Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
ty = ∑βjtxj
Для оценки β-коэффциентов применим МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=β1+rx1x2•β2 +... + rx1xm•βm
rx2y=rx2x1•β1 + β2 +... + rx2xm•βm
...
rxmy=rxmx1•β1 + rxmx2•β2 +... + βm
Для наших данных (берем из матрицы парных коэффициентов корреляции):
0.447 = β1 + 0.149β2 + 0.629β3
0.92 = 0.149β1 + β2 + 0.77β3
0.885 = 0.629β1 + 0.77β2 + β3
Данную систему линейных уравнений решаем методом Гаусса: β1 = 0.269; β2 = 0.809; β3 = 0.0926;
Стандартизированная форма уравнения регрессии имеет вид:
y0 = 0.269x1 + 0.809x2 + 0.0926x3
Найденные из данной системы β–коэффициенты позволяют определить значения коэффициентов в регрессии в естественном масштабе по формулам:
3. Анализ параметров уравнения регрессии.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов, исследованию абсолютных и относительных ошибок аппроксимации
Для несмещенной оценки дисперсии проделаем следующие вычисления:
Несмещенная ошибка ε = Y - Y(x) = Y - X*s (абсолютная ошибка аппроксимации)
| Y | Y(x) | ε = Y - Y(x) | ε2 | (Y-Yср)2 | |ε: Y| |
| 2.3 | 2.094 | 0.206 | 0.0424 | 2.8 | 0.0895 |
| 2.1 | 2.415 | -0.315 | 0.0991 | 3.509 | 0.15 |
| 2.9 | 2.736 | 0.164 | 0.027 | 1.152 | 0.0567 |
| 2.7 | 2.745 | -0.0447 | 0.002 | 1.621 | 0.0166 |
| 3.2 | 3.173 | 0.0271 | 0.000733 | 0.598 | 0.00846 |
| 3.4 | 3.494 | -0.0937 | 0.00878 | 0.329 | 0.0276 |
| 3.8 | 3.824 | -0.0235 | 0.000554 | 0.03 | 0.00619 |
| 4.2 | 4.144 | 0.0557 | 0.0031 | 0.0514 | 0.0133 |
| 4.2 | 4.573 | -0.373 | 0.139 | 0.0514 | 0.0887 |
| 4.5 | 4.474 | 0.0259 | 0.000669 | 0.277 | 0.00575 |
| 5.2 | 4.902 | 0.298 | 0.0886 | 1.505 | 0.0572 |
| 5.8 | 5.331 | 0.469 | 0.22 | 3.337 | 0.0809 |
| 4.7 | 4.804 | -0.104 | 0.0108 | 0.528 | 0.0221 |
| 5.5 | 5.232 | 0.268 | 0.0717 | 2.331 | 0.0487 |
| 5.1 | 5.66 | -0.56 | 0.314 | 1.269 | 0.11 |
| 1.029 | 19.389 | 0.781 |
Средняя ошибка аппроксимации
Оценка дисперсии равна:
se2 = (Y - X*Y(X))T(Y - X*Y(X)) = 1.03
Несмещенная оценка дисперсии равна:
Оценка среднеквадратичного отклонения (стандартная ошибка для оценки Y):
Найдем оценку ковариационной матрицы вектора k = S2 • (XTX)-1
Дисперсии параметров модели определяются соотношением S2i = Kii, т.е. это элементы, лежащие на главной диагонали
Показатели тесноты связи факторов с результатом.
Если факторные признаки различны по своей сущности и (или) имеют различные единицы измерения, то коэффициенты регрессии bj при разных факторах являются несопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с результатом, позволяющими ранжировать факторы по силе влияния на результат.
К таким показателям тесноты связи относят: частные коэффициенты эластичности, β–коэффициенты, частные коэффициенты корреляции.
Частные коэффициенты эластичности.
С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:
Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора хj на 1% от своего среднего уровня при фиксированном положении других факторов модели.
Частный коэффициент эластичности |E1| < 1. Следовательно, его влияние на результативный признак Y незначительно.
Частный коэффициент эластичности |E2| < 1. Следовательно, его влияние на результативный признак Y незначительно.
Частный коэффициент эластичности |E3| < 1. Следовательно, его влияние на результативный признак Y незначительно.
Стандартизированные частные коэффициенты регрессии.
Стандартизированные частные коэффициенты регрессии - β-коэффициенты (βj) показывают, на какую часть своего среднего квадратического отклонения S(у) изменится признак-результат y с изменением соответствующего фактора хj на величину своего среднего квадратического отклонения (Sхj) при неизменном влиянии прочих факторов (входящих в уравнение).
По максимальному βj можно судить, какой фактор сильнее влияет на результат Y.
По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Коэффициент βj может также интерпретироваться как показатель прямого (непосредственного) влияния j -ого фактора (xj) на результат (y). Во множественной регрессии j -ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).
Косвенное влияние измеряется величиной: ∑βirxj,xi, где m - число факторов в модели. Полное влияние j-ого фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата - rxj,y.
Так для нашего примера непосредственное влияние фактора x1 на результат Y в уравнении регрессии измеряется βj и составляет 0.269; косвенное (опосредованное) влияние данного фактора на результат определяется как:
rx1x2β2 = 0.149 * 0.809 = 0.1202
Сравнительная оценка влияния анализируемых факторов на результативный признак.
5. Сравнительная оценка влияния анализируемых факторов на результативный признак производится:
- средним коэффициентом эластичности, показывающим на сколько процентов среднем по совокупности изменится результат y от своей средней величины при изменении фактора xi на 1% от своего среднего значения;
- β–коэффициенты, показывающие, что, если величина фактора изменится на одно среднеквадратическое отклонение Sxi, то значение результативного признака изменится в среднем на β своего среднеквадратического отклонения;
- долю каждого фактора в общей вариации результативного признака определяют коэффициенты раздельной детерминации (отдельного определения): d2i = ryxiβi.
d21 = 0.45 • 0.269 = 0.12
d22 = 0.92 • 0.809 = 0.74
d23 = 0.88 • 0.0926 = 0.0819
При этом должно выполняться равенство:
∑d2i = R2 = 0.95
Множественный коэффициент корреляции (Индекс множественной корреляции).
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции.
В отличии от парного коэффициента корреляции, который может принимать отрицательные значения, он принимает значения от 0 до 1.
Поэтому R не может быть использован для интерпретации направления связи. Чем плотнее фактические значения yi располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,...,xm).
Таким образом, при значении R близком к 1, уравнение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат. При значении R близком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
Связь между признаком Y факторами X сильная
Расчёт коэффициента корреляции выполним, используя известные значения линейных коэффициентов парной корреляции и β-коэффициентов.
Коэффициент детерминации
R2 = 0.947
Коэффициент детерминации.
R2= 0.9732 = 0.947
4. Оценка значения результативного признака при заданных значениях факторов.
Y(0.0,0.0,0.0) = 0.8 + 0.32 * 0.0 + 0.65 * 0.0 + 0.11 * 0.0 = 0.8
V = X0T(XTX)-1X0
где
X0T = [ 1; 0.0; 0.0; 0.0]
Умножаем матрицы X0T и (XTX)-1
Умножаем полученную матрицу на X0, находим V = 3.28
Доверительные интервалы с вероятностью 0.95 для среднего значения результативного признака M(Y).
(Y – t*SY; Y + t*SY)
где t(15-3-1;0.05/2) = 2.201 находим по таблице Стьюдента.
(0.8 – 2.201*0.55; 0.8 + 2.201*0.55)
(-0.41;2.01)
C вероятностью 0.95 среднее значение Y при X0i находится в указанных пределах.
Доверительные интервалы с вероятностью 0.95 для индивидуального значения результативного признака.
(0.8 – 2.201*0.63; 0.8 + 2.201*0.63)
(-0.59;2.19)
C вероятностью 0.95 индивидуальное значение Y при X0i находится в указанных пределах.
5. Проверка гипотез относительно коэффициентов уравнения регрессии (проверка значимости параметров множественного уравнения регрессии).
Число v = n - m - 1 называется числом степеней свободы. Считается, что при оценивании множественной линейной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.
1) t-статистика
Tтабл (n-m-1;α/2) = (11;0.025) = 2.201
Находим стандартную ошибку коэффициента регрессии b0:
Статистическая значимость коэффициента регрессии b0 не подтверждается.
Находим стандартную ошибку коэффициента регрессии b1:
Статистическая значимость коэффициента регрессии b1 подтверждается.
Находим стандартную ошибку коэффициента регрессии b2:
Статистическая значимость коэффициента регрессии b2 подтверждается.
Находим стандартную ошибку коэффициента регрессии b3:
Статистическая значимость коэффициента регрессии b3 не подтверждается.
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(bi - ti Sbi; bi + ti Sbi)
b0: (0.8 - 2.201 • 0.55; 0.8 + 2.201 • 0.55) = (-0.42;2.02)
b1: (0.32 - 2.201 • 0.14; 0.32 + 2.201 • 0.14) = (0.00219;0.64)
b2: (0.65 - 2.201 • 0.12; 0.65 + 2.201 • 0.12) = (0.39;0.91)
b3: (0.11 - 2.201 • 0.22; 0.11 + 2.201 • 0.22) = (-0.37;0.59)
6. Проверка общего качества уравнения множественной регрессии.
Оценка значимости уравнения множественной регрессии осуществляется путем проверки гипотезы о равенстве нулю коэффициент детерминации рассчитанного по данным генеральной совокупности: R2 или b1 = b2 =... = bm = 0 (гипотеза о незначимости уравнения регрессии, рассчитанного по данным генеральной совокупности).
Для ее проверки используют F-критерий Фишера.
При этом вычисляют фактическое (наблюдаемое) значение F-критерия, через коэффициент детерминации R2, рассчитанный по данным конкретного наблюдения.
По таблицам распределения Фишера-Снедоккора находят критическое значение F-критерия (Fкр). Для этого задаются уровнем значимости α (обычно его берут равным 0,05) и двумя числами степеней свободы k1=m и k2=n-m-1.
2) F-статистика. Критерий Фишера.
Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение Y.
Более объективной оценкой является скорректированный коэффициент детерминации:
Добавление в модель новых объясняющих переменных осуществляется до тех пор, пока растет скорректированный коэффициент детерминации.
Проверим гипотезу об общей значимости - гипотезу об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:
H0: R2 = 0; β1 = β2 =... = βm = 0.
H1: R2 ≠ 0.
Проверка этой гипотезы осуществляется с помощью F-статистики распределения Фишера (правосторонняя проверка).
Если F < Fkp = Fα; n-m-1, то нет оснований для отклонения гипотезы H0.
Табличное значение при степенях свободы k1 = 3 и k2 = n-m-1 = 15 - 3 - 1 = 11, Fkp(3;11) = 3.59
Отметим значения на числовой оси.
| Принятие H0 | Отклонение H0, принятие H1 |
| 95% | 5% |
| 3.59 | 65.52 |
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим и уравнение регрессии статистически надежно
Оценка значимости дополнительного включения фактора (частный F-критерий).
Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличить долю объясненной вариации результативного признака. Это может быть связано с последовательностью вводимых факторов (т. к. существует корреляция между самими факторами).
Мерой оценки значимости улучшения качества модели, после включения в нее фактора хj, служит частный F-критерий – Fxj:
где m – число оцениваемых параметров.
В числителе - прирост доли вариации у за счет дополнительно включенного в модель фактора хj.
Если наблюдаемое значение Fxj больше Fkp, то дополнительное введение фактора xj в модель статистически оправдано.
Частный F-критерий оценивает значимость коэффициентов «чистой» регрессии (bj). Существует взаимосвязь между частным F-критерием - Fxj и t-критерием, используемым для оценки значимости коэффициента регрессии при j-м факторе:
Date: 2015-09-22; view: 4868; Нарушение авторских прав